Game Theory Lecture
Introduction
The following chapter will consider Game Theory and group co-operation in economics. Game theory looks to present models of conflict and cooperation which may exist between intelligent, and rational decision-makers; actors in the game. Essentially, it is a study on interaction, considering how economic agents produce outcomes with respect to their preferences (or utilities) of those agents. The most well-known example of game theory can be seen as the ‘Prisoner’s Dilemma’. The games showcase why two completely ‘rationale’ actors might not cooperate, even though it is in their best intentions to do so. The visual below displays a standard game between two prisoners. In this example, there are two prisoners who both should decide whether they remain quiet, or confess. The important factor to mention here is that while it would be better if both prisoners remained quiet, neither of them know what the other will decide; there is no information flow between the decision-makers.
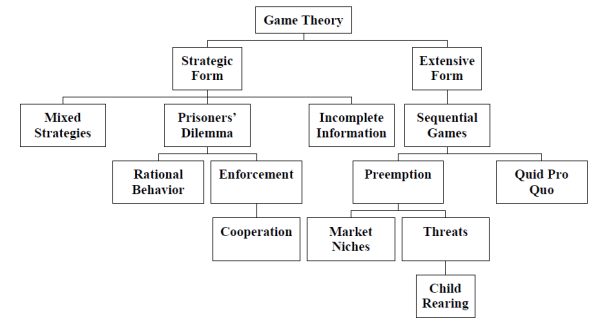
Figure 1 - Game Theory Map
Basics of Game Theory
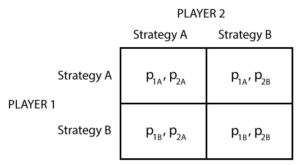
To begin, we will consider the map which has been presented above; detailing the main topics mentioned within game theory. Initially, there is the difference between a strategic form and a extensive form. As suggested, the strategic form is a game whereby the player is attempting to benefit themselves by a single move, usually represented in a ‘Matrix’ as will be shown later in the chapter. The image below depicts a version of a matrix, showing the potential plays that each player can make:
Figure 2 - Example of Game Theory.
A strategic form is the right choice for simultaneous games whereby both players make their move simultaneously given the information which they have available. As we move further down in the map above, we have the incomplete information, Prisoner’s Dilemma, and mixed strategies. The incomplete information refers to the idea of non-cooperation between players, suggesting that each may have incomplete, or limited information above the other player. This is the case when it comes to the Prisoner’s Dilemma. In this game, the two players are non-cooperative, and so must make their decision alone without full information over how the other player will play. This will be discussed later in the chapter. However, what this does bring into play is the idea of Rational Behaviour. The definition here would be that a rational behaviour decision-making process is based on making choices that result in the most optimal level of benefit or utility for the individual.
Finally, there is the consideration of a mixed strategy. This type of strategy could be seen when there are two players who will not agree on an equilibrium, meaning that a mixed strategy may be adopted which should end with a balance, essentially maximising the utility based on the different opinions. So, the example below considers a situation between a man, and the woman choosing what to do over the weekend. Neither can agree what to do, with the woman preferring to go shopping, and the main preferring to watch the boxing. However, what can also be mentioned from the table below is that utility would be zero for both if they each did something separately.
Figure 3 - Mixed Strategy within Game Theory.
With this in mind, it could be considered that there needs to be a compromise, which in turn could be seen as a mixed strategy. So, one solution could be that the man decides to go shopping, in turn reducing his own utility, but raising that of the female. Essentially, the compromise will see one player accept a lower utility.
Need Help With Your Economics Essay?
If you need assistance with writing a economics essay, our professional essay writing service can provide valuable assistance.
See how our Essay Writing Service can help today!
Extensive Form
The other option to take was the extensive form. An extensive form game could be visualised as a tree, presenting every possible state of play which can be played in the game. This is shown in the image below, detailing the choice between two organisations. What is interesting to note here is that the game is played player by player; sequential as opposed to simultaneously. So, in the model below it can be noted that organisation A makes the first play, choosing to enter a new market or stay away. If organisation A does enter the new market, then organisation B will have their turn, choosing to either accommodate the new competition, or fight. Linking this back with Figure 1 above, it could be noted that organisation B may look to fight the new entrant, pre-empting any competition to its own market share:
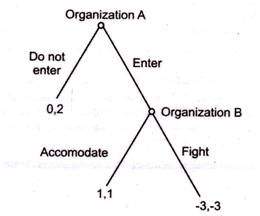
What should also be noted here is that sequential games may come with multiple turns. For instance, if organisation B chooses to fight, then organisation A may change its strategy to deal with heightened competition. Considering this, these games can go on for many years, as opposed to the Prisoner’s Dilemma which is a single-turn, simultaneous game with a direct outcome.
Figure 1 also mentions ‘Quid pro quo’ a situation whereby cash, concessions may be given with strings attached. For instance, examples can be noted in the social welfare programmes of many countries. For instance, the UK government give out ‘jobseekers allowance’ in exchange for the claimants proving that they are searching for work. Such examples can also be seen in the business world. Phrases with similar meanings include: "give and take", "tit for tat", and "you scratch my back, and I'll scratch yours". Taking the example above with organisation A & B, organisation B may choose not to fight organisation A in the market as long as organisation A remains out of certain locations. We can look at this another way. Consider airlines Ryanair and EasyJet at Manchester Airport. EasyJet chooses to expand its operations at the airport, which could lead to Ryanair responding by lowering its own prices and expanding its own routes. However, Ryanair may only do this if EasyJet directly competes. So, EasyJet may decide to not expand into the Manchester-Paris route, and Ryanair in turn may decide not to expand into the Manchester-Alicante route.
Game Theory (Prisoner’s Dilemma)
The idea behind games theory came from research into duopolies and the way in which two businesses will operate in the industry. In such markets, the business will behave strategically, so each business must think about what the other firm may do in a bid to decide what it should do itself. The first major book in game theory, published in 1944, was ‘Theory of Games and Economic Behavior’, by John von Neumann (1903-1957) and Oskar Morgenstern (1902-1977). Basically, we can consider that a group of people (or teams, firms, armies, countries) are in a game if their decision problems are interdependent, in the sense that the actions that all of them take influence the outcomes for everyone.
The most well-known of all these games could be seen as the Prisoner’s Dilemma. To set the scene here consider that a crime has been committed. There are two convicts, both arrested for the crime. Each person has the chance to cooperate, or defect (shown below):
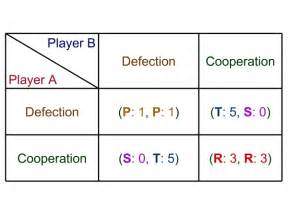
It could be considered from the options above that the best option will be for both to ‘Defect’; essentially both lie, leading to each receiving 1 year. However, the main issue with this is that the Prisoner’s Dilemma assumes no contact between the two players. Essentially, Player A does not know what Player B will do as there is no co-operation. So, if Player A decided to defect and Player B then co-operated, Player A would be looking at 5 years in prison while Player B is let off. The same is possible for Player B. With this in mind, both players would look to choose an option which offers the best possible set of solutions. In the example above, this would be to co-operate given that the maximum sentence will be 3 years as opposed to 5 years.
Ultimately, the ‘Nash Equilibrium’ (discussed later) may be for each to remain silent, shortening each of their sentences. However, when considering a dominant strategy, it may be considered that the iterated dominance would be for each person to speak out, in turn pushing the other player to also speak. Essentially, iterated dominance is seen as the dominant strategy for that individual player, in the case above being for the player to speak out, and potentially receive 0 years. The main difference to these two options is the level of knowledge, or collusion that exists between the parties. As mentioned with the case above, there is no interaction, and so each player can only predict the movement of the other player, rather than know for certain.
Example of Brexit
The recent Brexit vote can be viewed as a real-world example of the Prisoner’s Dilemma; however, the main difference here could be that each side will have time to discuss their options. As of June 24, 2016, the UK and the European Union face a real-world prisoner's dilemma; by invoking Article 50 means that the country has a two-year period to negotiate its economic and political relationship with the EU. As is expected, both sides are keeping self-interests in mind when approaching the negotiating table.
For example, the UK will seek to obtain the advantages of the EU's single market with none of the potential costs. Meanwhile, the EU has called for consequences in regards to the UK’s exit vote, wanting to make an example for any other country thinking of leaving. However, if both sides decide to work together to come to an agreement that is mutually beneficial, the prisoner's dilemma can be circumvented and both sides can prosper. If both sides hold fast to personal interests, neither side benefits; it becomes a zero-sum game.
Iterated Dominance
This chapter will now consider the idea of the iterated dominance strategy.
To set the scene, the question asked for a game which is simultaneous, non-co-operative, and one shot. Essentially, the example which will be used here is the choice by two businesses to invest $100Million to expand production. As mentioned in the question, this is done with no knowledge of the action of the other; namely there is no cooperation which may involve collusion to protect capacity/ price in the market, like what could be seen currently in the oil market with OPEC, mentioned by Camerer (2010). With this, the following table looks like:
|
X Plc |
||||
|
Y Plc |
Invest |
50% Investment |
Don’t Invest |
|
|
Invest |
5, 5 |
10, 4 |
25, -10 |
|
|
Don’t Invest |
-10, 25 |
-8, 10 |
0,0 |
|
Taking the above into account, the best strategy above would be for each player to invest given the payoff, however the best solution would be if they invested and the other player didn’t, providing the greatest benefit for the investor. It must also be noted that X Plc., has three potential strategies which also allows for a part-investment. This is like the ‘Prisoner’s Dilemma’, with the expectation that each player will have their dominant strategy which can be used to maximise their own result.
However, this game could potentially be solved by the iterated deletion of dominant strategies. The main idea here is that by understanding the dominant strategies, a prediction can be made into the choice of the business. Iterated dominance is built on two main assumptions. The first is even if the player doesn’t have a dominant strategy, they may still have one which dominates another, for instance, by investing, Y Plc., has a higher payoff in all instances. So, what is being mentioned here is that instead of using a superlative statement (i.e. Investing in the best option available), a comparative statement can be used; namely investing would be a better option than not investing. For Y Plc., given that the payoff is higher in all instances with investing, we can say that the ‘Invest’ strategy dominants the ‘Don’t Invest’ strategy. The second idea is then over the transition from some dominant strategies to iterated dominance; seen as anticipating the moves of the other player. To simplify this, consider that Y Plc., benefits in all instances if it chooses to ‘Invest’. With this, X Plc., should recognised that investing is a strictly dominant strategy for Y Plc., and so in this case there is no chance that Y Plc., will consider the ‘Don’t Invest’ strategy. Ultimately, it is rational decision for Y Plc., to invest under all circumstances. So, by eliminating the ‘Don’t Invest’ move, X Plc., reducing the number of outcomes, helping make its own decision.
This can then be taken down further. X Plc., can now consider its own position, and through the table above it can be noted that the largest pay-off will come from X Plc., only moving forward and choosing to ‘Invest’ itself. In some cases, this result can differ from the Nash Equilibrium which would be seen when both players adopt a position which is the best response to each other.
The constructed example above has shown that players can use iterated deletion of dominated strategies by predicting the choice of the other player by considering their logical choices. So above, X Plc., was able to see that it would not be logical for Y Plc., to choose ‘Don’t Invest’ given that all combinations offer a worse result for Y Plc.
Nash equilibrium
Nash Equilibrium can be defined as a concept of game theory where the optimal outcome of the game is where no player has an incentive to deviate from their chosen strategy, even after considering their opponent’s choice. Overall, the individual can receive no incremental benefit from changing actions; under the assumption that all other players keep their strategy constant. A game may have multiple Nash Equilibria or none at all. The showcase the Nash Equilibrium let’s consider the example below
|
Player 2 |
|||
|
Player 1 |
I |
A |
|
|
I |
2,1 |
0,0 |
|
|
A |
0,0 |
1,2 |
|
To find the Nash equilibria, we examine each action profile in turn.
(I, I) Neither player can increase her payoff by choosing an action different from her current one. So, this action profile is a Nash equilibrium.
(I, A) By choosing A rather than I, player 1 obtains a payoff of 1 rather than 0, given player 2's action. So, this action profile is not a Nash equilibrium. [Also, player 2 can increase her payoff by choosing I rather than A.]
(A, I) By choosing I rather than A, player 1 obtains a payoff of 2 rather than 0, given player 2's action. So, this action profile is not a Nash equilibrium. [Also, player 2 can increase her payoff by choosing A rather than I.]
(A, A) Neither player can increase her payoff by choosing an action different from her current one. So, this action profile is a Nash equilibrium.
We can conclude that the game has two Nash equilibria, (I, I) and (A, A).
In the Prisoner’s Dilemma shown above, there is one ‘Nash Equilibria’ to consider. However, in some games there could be multiple, confusing the decision-making process. For instance, consider the example of a game-show, whereby two players have a box with 4 squares, three are which are blue and one which is red. The idea behind the show is that players win a prize if they both select the same square, unaware of what the other has selected. This is where the idea of a ‘Focal Point’ can be considered, introduced by American economist Thomas Schelling. In the example, the solution could appear somewhat simple given that each may choose the ‘Red’ square given that it individual, and is the most salient and noticeable option. Schelling, in his work illustrated this concept with the following problem: "Tomorrow you have to meet a stranger in NYC. Where and when do you meet them?" This is a coordination game, where any place and time in the city could be an equilibrium solution. Schelling asked a group of students this question, and found the most common answer was "noon at (the information booth at) Grand Central Terminal". Similar could be considered in the business world whereby two businesses may base their own decision of the most common response.
Focal points can be useful for solving matching games with multiple Nash equilibria. For instance, focal points can be used to develop social norms. Consider the example below whereby two drivers must choose which side of the road to drive on. Essentially, there are two Nash Equilibria here, with the drivers escaping a car crash if they both choose to drive on the same side, so R,R or L,L; otherwise there will be a crash.
|
Driver 1 |
|||
|
Driver 2 |
R |
L |
|
|
R |
1, 1 |
0, 0 |
|
|
L |
0, 0 |
1, 1 |
|
In this case, the focal point is really a social norm, for instance, in the UK all drivers are taught, and so programmed to drive on the left-hand side. In this case, the focal point can be used to solve matching games, with the point always pointing to driving on the left-hand side. To conclude, focal points are useful as they are noticeable, and in the case mentioned above will turn into a social norm.
Different types of equilibrium - Zero Sum Games
Following on from the explanation above of the Prisoner’s Dilemma, several other games could be considered. For instance, there could be games which are classed as ‘zero sum’ games whereby the gain of one player is offset by a loss from another. For instance, consider two businesses operating in a market worth £100Million. Business B chooses to spend 10% more on its marketing, while Business A chooses to remain the same. The result would be that Business B gains £9Million in sales, while Business A loses £9Million sales; ultimately the game is ‘zero sum’ as the gains posted by Business B are the losses posted by Business A.
Non-cooperation games
Non-cooperative games are defined as games where players make their decisions independently. Thus, while players could cooperate, any cooperation must be self-enforcing. For instance, a good example could be seen as the game ‘Rock, Paper, Scissors’ - you don’t tell each other what you are going to choose as that defeats the objective of the game. A good example of this could be considered in the oil market with OPEC and non-OPEC. The current strategy adopted calls for production from all OPEC members to be capped at 32Million bpd, a target which is enforced by all for members for the benefit of the market. However, what the OPEC example also shows us is that for the benefits to be realised, cooperation would need to include all in the market. So, while OPEC have cooperated to cut production, higher prices in the short-term have only enticed non-OPEC producers to increase their own production, leading to price falls; keeping oil prices low. Non-cooperative games can become difficult to consider given that there is also the need to take into account bargaining power of the players.
On the opposite end, a cooperative game is one where players are convinced to adopt a strategy through agreements/ negotiations between players. These games may have external forces which drive cooperation, for instance contract law, regulation.
Multi-move Games - Sequential Games
When it comes to mentioning game theory in the business world, it becomes hard to imagine a game where there is only one move. When we imagine businesses games with multiple players, each may take multiple moves over several periods/ years; in turn competing with each other and responding to changes in the marketplace. For instance, consider the UK airline market. A move by Ryanair to reduce prices in the market, while other such as EasyJet may keep theirs the same may not spell the end of the game. As mentioned above, there are multiple moves to consider. After seeing Ryanair’s price reductions in the market, EasyJet itself can quickly respond with its own price reductions if needed; or move forward with another strategy which may be focused on marketing etc. These can also be noted as sequential moves in the game.
In game theory, a sequential game is where one player chooses their move before the other. With this in mind, the expectation would be that after the first player has chosen, player 2 has a greater knowledge, and so could be better informed into how to respond. Given this, there is an element of strategy to consider. So, taking the example above with X Plc., and Y Plc, consider that Y Plc., made their move first, choosing to ‘Invest’. With this, X Plc., now needs to consider how to respond, be it in the short-term, or potentially in the long-term. Taking the new information, X Plc., could potentially consider some strategic analysis into how the investment from Y Plc., may impact on the market, which in turn may make them better informed over their decision. Let’s consider the example used above:
|
X Plc |
||||
|
Y Plc |
Invest |
50% Investment |
Don’t Invest |
|
|
Invest |
5, 5 |
10, 4 |
25, -10 |
|
|
Don’t Invest |
-10, 25 |
-8, 10 |
0,0 |
|
So, Y Plc., has chosen to invest, adding capacity onto the market. X Plc., must now choose its sequential move; while the optimal solution would be for the business to also ‘Invest’, bringing in “5”, there are some issues which may arise. So, X Plc., may gain greater knowledge of Y’s investment plans, potentially the size of the new plant, and the additional capacity which could be put in the market. With this, the actual financials of the project may change; if the capacity added from Y Plc., is higher than predicted, then this may have a greater impact on the price, potentially leading to price falls which could affect the profitability of the project. It must be mentioned here that when it comes to ‘games’ involving investments and businesses, there is the expectation that a business may have undertook some strategic analysis. An example here could be undertaking Net Present Value analysis to consider whether the investment decision is viable, and acquires the required rate of return (Johnson et al, 2008).
Strategic moves also become important when retaliation can be considered. For instance, consider a ‘game’ between Ryanair and EasyJet. Ryanair moves first and decides to cut prices on its routes. EasyJet now has a choice to make, be it cut its own prices or keep them the same. If both acted at the same time, EasyJet may have considered the same strategy, cutting its own prices. However, with EasyJet waiting, there is the potential for the airline to ‘sit and wait’; seeing the initial impact that Ryanair’s price cut has on the revenue and sales for the airline. If the move by Ryanair proves detrimental to EasyJet’s sales, then the airline should cut its own prices to remain competitive, however by doing this the airline potentially moves into a long-term ‘game’ where Ryanair retaliates with further price cuts; a potential ‘price war’. If this proceed, then the long-term implication could be that both airlines lose out as they reduce their profitability. Ultimately, strategy is important to consider when the ‘game’ begins to impact the industry. For EasyJet, there is an opportunity cost to make with their sequential move. On one hand, by cutting prices they are diluting their profitability on all customers, however by keeping prices the same, they are at risk that some customers move to Ryanair. EasyJet needs to analyse its current service offering i.e. routes, compared with Ryanair to calculate which is the best response.
A way to visualise this could be in the game tree shown below.

Figure 4 - Visualisation of a ‘Game Tree’ - these can get bigger depending on the number of decisions which can be made by the players. There could also be more than two players involved, as we see with many competitive, and dynamic markets.
The importance of knowledge, noting how players can make more informed choices in sequential games given the increase in information which is available. As noted above, some of these ‘games’ can go on for many years. ‘Dynamic Games’ can also be considered. To provide a definition, a dynamic game can arise between players (individuals, firms, countries, animals, etc.) when the strategic interactions among them recur over time and decisions made during one period affect both current and future payoffs; so as mentioned the potential for overcapacity affecting long-term prices/ income, or for a decision in the fishing sector for instance affecting the long-term quota’s. Dynamic games provide conceptually rich paradigms and tools to deal with these situations. Consider game theory in regards to investments, noting how investors may make strategic moves based on the moves of others to reflect changes in the market; be it investing into a certain asset class, buying/ selling equities etc. Ultimately, in this case, the strategic move is important for the investor to maximise their returns, essentially their pay-off.
When it comes to sequential games, the guiding principle could be noted as ‘think forwards and reason backwards. The strategist needs to consider three importance aspects; (1) being what the competitor desires as their outcome, (2) being the sequence of moves that a competitor may make based on that desired outcome, and so with this (3) being the most advantageous strategy for itself. In doing this, the player needs to bear in mind that other players (competitors) will have different strategic capabilities, and so from this will have different dominant strategies. For instance, it has been mentioned above that Ryanair clearly has the capabilities to offer a low-cost airline model, and so with this its dominant strategy will be to increase income through low-prices, driving volume as opposed to raising prices. On the other hand, airlines such as British Airways may be more focused on service quality given their capabilities, allowing them to charge a premium price. It is also important to note the importance of strategic moves as logically it can be considered that the rules of the game can change, especially in sequential games as competitors gain more information. Consider the example above with Ryanair dominating the market with a price-based strategy. To reduce the risk of their income being diluted, come airlines may seek to change the rules of the game through (1) clearer differentiation between their product offering and that of Ryanair, allowing for a differentiated price; (2) being more incentives for customer loyalty, or (3) being transparent pricing to the consumer, showing the extra services which they may be paying for.
Single/ Multi-Player Games
Following on from the above, we can also consider games which have multiple players. While game theory was originally developed on the back of duopoly behaviour in markets; changes now mean there are many more competitors, and so players within the market. For instance, consider a flight between London - Tokyo. Multiple players can have a position in the market, be it the direct operators such as British Airways, other ‘hub’ airlines such as Emirates and even the low-cost carriers such as EasyJet who may offer connections in other European cities. This creates a game whereby there are more than two players, creating the potential for many more combinations of outcomes.
For instance, consider the construction of a rota in a 24/7 retail outlet with 100 employees. The payoff associated with different working hours may differ based on the pay, and the utility gained/ lost from working the shift. Essentially, this is a game involving 100 players who will all have their own strategies based on individual preferences.
Need Help With Your Economics Essay?
If you need assistance with writing a economics essay, our professional essay writing service can provide valuable assistance.
See how our Essay Writing Service can help today!
Conclusion
So, the following chapter has looked to discuss game theory, presenting models of conflict and cooperation which may exist between intelligent, and rational decision-makers; actors in the game. The most basic form of a game could be considered as the Prisoner’s Dilemma; essentially two players playing a simultaneous game with two options, and limited information. In this case, the player will choose the option which maximises their own position based on the information available. However, as noted throughout the chapter, there are numerous examples in the business world where this will not hold. For instance, there are instances whereby businesses may have greater information about each other’s motives, and options when it comes to playing a game. For instance, management at Ryanair will have access to publicly published financial information from EasyJet, as well as shareholder information which could give them some indication over how they may act. Furthermore, there is also the consideration that many games are not simultaneous; for instance, Ryanair may seek to act before EasyJet to compete, or after EasyJet to protect its market etc. Leading on from this there is also the consideration that games in the business world may have multiple moves; continuing for years as businesses seek to compete.
It may also be considered that real-world games may have multiple players as opposed to two. For instance, the example above made note of how a staff rota in an organisation could be seen as a ‘game’, potentially involving hundreds of employees. Essentially, each player will have their own strategy, be it to work a certain shift, day-off, overtime etc.
Ultimately, while game theory can be applied to many situations in life, and in business, the factors influencing the game; i.e. information, number of players etc., are all variable, which in turn will impact on how the game is played (simultaneous, sequential) as well as the results expected by the players. Ultimately, each player will seek for the outcome which benefits them the most, however if there is a lack of information, the player may turn to a dominant strategy, or a Nash Equilibrium which offers them the best return in all situations, based on the choices of the other players.
Questions
- Define the following terms:
Nash Equilibrium - …………………..
Dominant Strategy - ………………....
Mixed Strategy - ……………………..
Zero-Sum Game - ……………………
- Determine if either player below has a dominant strategy? Why, or why not?
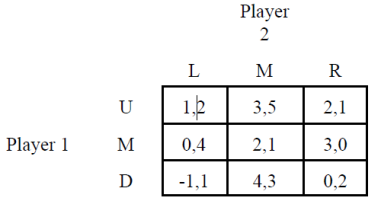
- Does the example below display Nash Equilibrium? Why, or why not?
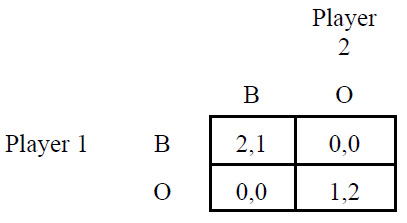
Practical Example
The following chapter considers ‘Game Theory’. To provide a definition, game theory looks to present models of conflict and cooperation which may exist between intelligent, and rational decision-makers; actors in the game
Study into ‘Game Theory’ is widely regarded as starting in the mid-19th century with the publication in 1838 of Augustin Cournot's ‘Researches into the Mathematical Principles of the Theory of Wealth’, where he attempted explain the underlying rules governing the behaviour of duopolies. However, it was with the publication in 1944 of John von Neumann and Oskar Morgenstern's The Theory of Games and Economic Behaviour that the modern principles of game theory. Game theory has been widely applied to the behaviour of producers with a few or only one competitor. At first, we can ask - What is a game?
All games have the following:
- Rules, which govern conduct of the players
- Pay-offs, such as win, lose or draw
- Strategies, which influence the decision-making process.
When we consider such games in real-world, business scenarios, we can consider several strategies:
Decisions on price and output, such as whether to:
- Raise
- Lower, or
- Hold.
Product decisions such as:
- Keep existing products
- Develop new ones
- Spend more on advertising, etc.
The most widely considered game is the Prisoner’s Dilemma, a game in which two players play a simultaneous game. They choose whether to ‘Cooperate’ or ‘Defect’. However, what must be remembered here is that in this game there is no interaction between the players; each make their own decision with no communication.
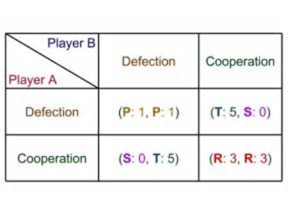
It could be considered from the options above that the best option will be for both to ‘Defect’; essentially both lie, leading to each receiving 1 year. However, the main issue with this is that the Prisoner’s Dilemma assumes no contact between the two players. Essentially, Player A does not know what Player B will do as there is no co-operation. So, if Player A decided to defect and Player B then co-operated, Player A would be looking at 5 years in prison while Player B is let off. The same is possible for Player B. Both players would look to choose an option which offers the best possible set of solutions. In the example above, this would be to co-operate given that the maximum sentence will be 3 years as opposed to 5 years. It could be considered that there would be one option for each, one which would be considered as the ‘Nash Equilibrium’, being that the player chooses to cooperate, given that such a move offers the best return for the player in the case that the other player picks either. To provide a definition of Nash Equilibria:
Nash Equilibrium can be defined as a concept of game theory where the optimal outcome of the game is where no player has an incentive to deviate from their chosen strategy, even after considering their opponent’s choice.
In some games, there could be multiple Nash equilibriums, while in others there could be none. While the Prisoner’s Dilemma does present a theoretical example of game theory, real-world situations may have several differences. First is the consideration that some games will not be simultaneous, instead they will be sequential. For instance, consider Ryanair and EasyJet; the expectation in a game would be that one player acts, which in turn may cause the other player to act before, or after to protect their own strategy. It could then be considered that players will have greater information on each other. For instance, prior to making their decision, Ryanair may be able to collect, and collaborate publicly available information on EasyJet such as financial data, press releases, route maps etc.; helped them with potentially predicting EasyJet’s move and benefitting them when it comes to making their own decision.
The importance of knowledge, noting how players can make more informed choices in sequential games given the increase in information which is available. Some of these ‘games’ can go on for many years. These can be visualised by using a decision tree style layout, shown below:

‘Dynamic Games’ can also be considered. To provide a definition, a dynamic game can arise between players (individuals, firms, countries, animals, etc.) when the strategic interactions among them recur over time and decisions made during one period affect both current and future payoffs; so as mentioned the potential for overcapacity affecting long-term prices/ income, or for a decision in the fishing sector for instance affecting the long-term quota’s
Another factor to consider is that many games in the business world which impact on an overall market may involve more than two players. For instance, consider a flight between London - Tokyo. Multiple players can have a position in the market, be it the direct operators such as British Airways, other ‘hub’ airlines such as Emirates and even the low-cost carriers such as EasyJet who may offer connections in other European cities. This creates a game whereby there are more than two players, creating the potential for many more combinations of outcomes.
Finally, it could also be considered that some games could be cooperative, while others non-cooperative. Non-cooperative games are defined as games where players make their decisions independently. Thus, while players could cooperate, any cooperation must be self-enforcing. For instance, a good example could be the game ‘Rock, Paper, Scissors’ - you don’t tell each other what you are going to choose as that defeats the objective of the game. On the opposite end, a cooperative game is one where players are convinced to adopt a strategy through agreements/ negotiations between players. So, OPEC could be considered as cooperation given that all members negotiate the production of oil from the group to maintain supply, and price. However, recently the increase in non-OPEC production has changed the market, leading to a non-cooperative game between OPEC and non-OPEC producers.
Cite This Module
To export a reference to this article please select a referencing style below: