ANN for Prediction of Product Selectivity in Biological Sulfide removal
| ✅ Paper Type: Free Essay | ✅ Subject: Chemistry |
| ✅ Wordcount: 1938 words | ✅ Published: 18 Jan 2018 |
Abstract
Artificial neural networks (ANNs) is applied for prediction of product selectivity in biological sulfide removal. An experimental setup is constructed for investigation of biological sulfide removal in a fed batch bioreactor. In this process, sulfide is biologically converted into elemental sulfur and sulfate by the bacterium Thiobacillus thioparus. In addition, thiosulfate is produced in a side reaction. The effect of various parameters (dissolved oxygen, concentration of bacteria and sulfide load) is investigated on the types of products. The main product is elemental sulfur at low dissolved oxygen or at high sulfide loads and also more sulfates are produced at high dissolved oxygen. At high concentration of bacteria, sulfur and sulfate selectivity are increased, and thiosulfate selectivity is decreased. By using gathered experimental data, an artificial neural network model is developed to calculate the selectivity of products at different operating conditions. The comparison between proposed ANN model and the experimental data demonstrates a great precision of the model.
Introduction
Hydrogen sulfide as an extremely toxic gas is emitted by many industries such as oil, gas and petrochemical industries [1]. It has potential for the damaging nervous system at low-dose exposures. Furthermore, sulfide is highly corrosive and has a very unpleasant odor. The threshold limit value for air 0.5–10 ppbv [2], natural gas 4 ppmv [3] and for fresh or salty water fish is 0.5 ppm [4].
In the recent years, biological sulfide removal at ambient temperature and pressure has been investigated as an alternative to the conventional methods. A review on the bacteria of the sulfur cycle was discussed by Tang et al which contributes to a better understanding of the process [7]. Also, a review of the biological removal of H2S from gas streams was studied by Sayed et al [8]. Several microorganisms, namely sulfur compound oxidizing bacteria (SOB), are capable of oxidizing H2S at ambient temperatures and pressures.
Different types of bioreactors are used for biological sulfide removal, the more common types are: bioscrubber, biotrickling filter, and biofilter. In the last two processes, the H2S-containing gas passes through a moist, packed bed of particles, which are coated by microorganisms. The biotrickling filter, and biofilter are proper for low sulfide capacity, which the sulfide is mainly converted to sulfate [8]. In the case of biological H2S removal from natural gas, the bioscrubber is more preferred.
In a bioscrubber, H2S is washed from the natural gas stream by an alkaline such as NaOH (Eqs. 1 and 2) in a gas absorber, then the rich alkaline solution is sent to an agitated bioreactor where the sulfide ions (HS–) are converted to elemental sulfur or sulfate (Eqs. 3 and 4). The produced elemental sulfur is separated by sedimentation [8-11]. Production of elemental sulfur is preferred since it is less harmful than sulfate. Furthermore, hydroxyl ions, consumed in the absorption of H2S in the alkaline liquid, are regenerated upon oxidation of sulfide to elemental sulfur (Eq. 3). Also, elemental sulfur is easily separated by sedimentation.
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
In addition to the biological reactions, dissolved sulfide can react with S0 to produce polysulfide ions (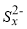 ), according to Eq. 5, and
), according to Eq. 5, and  ions are abiotically oxidized to S0 and
ions are abiotically oxidized to S0 and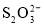 , according to Eq. 6 [12].
, according to Eq. 6 [12].
|
|
(5) |
|
|
(6) |
Teder [13] has shown that the chain length of polysulfide ion (Sx2-) increases with increase of temperature (x = 5.0 at 25 °C and x = 6.5 at 80 °C). At moderate alkaline conditions, the average chain length of polysulfide (x) varies from 4.6 to 5.5 [12-15].
The product selectivity in the biological sulfide removal process depends on different parameters such as bacteria concentration, sulfide load to the bioreactor and dissolved oxygen [*** Roosta]. This study investigates the applicability of artificial neural networks (ANNs) for the prediction of the biological sulfide removal performance in a fed batch bioreactor.
Materials and Methods
In this study, Thiobacillus thioparus (DSMZ 5368) was used as sulfur oxidizing bacteria for producing elemental sulfur in the biological sulfide removal process.In this regards, a bioreactor with total volume of 3.8 liter operated under fed batch conditions was used, as shown in Figure (1). During all experiments, the temperature was controlled at 30±0.3 °C, and the pH was controlled at 8±0.2 using 1N HCl and 1N NaOH solutions. Dissolved oxygen (DO) as a manipulated variable was changed between 0.5 and 6 ppm and controlled using nitrogen and oxygen injection. The bioreactor was charged with 2000 cc of the medium inoculated with biomass. After stabilizing of the temperature in the bioreactor at 30 °C, feeding of the sulfide solution was started. The concentration of sulfide was determined based on the methylene blue method proposed by Trüper and Schlegel [16], by using a spectrophotometer (Zeiss) at 665 nm. The sulfide solution was injected to the bioreactor by an infusion pump (JMS OT-701), after calibration of the pump. During the experiments, the sulfide solution is applied at different flow rates (between 1.5 and 23 ml h-1) to achieve different HS– load (between 0.5 and 4.0 mmolL-1h-1). The flow rate of recirculating gas was adjusted to 15 L min-1 and was spread by a diffuser; this caused a good mixing of the broth.
The concentration of sulfur compounds were measured during the process. In this regards, the total concentrations of sulfide (HS– and polysulfide) were determined based on the methylene blue method [17]. The concentration of polysulfide was determined based on Teder [14] method. The concentration of sulfide (HS–) is the difference between total sulfide concentrations and polysulfide concentration. The concentration of sulfate was determined via the turbiditimetry method at 420 nm [17], and the thiosulfate concentration was determined via the methylene blue method at 760 nm [18]. Finally, the concentration of elemental sulfur is calculated by the mass balance on sulfur.
The present study investigates the effect of operating variables: dissolve oxygen (DO) value (0.5 – 4 ppm), HS– load (0.5 – 4 mmol L-1 h-1) and optical density (OD) of bacteria (0.4 – 0.6) on the sulfide removal and product selectivity.
ANN
Artificial Neural Networks (ANNs) with different structures has been proven to be universal function approximators. The major advantage of ANN model is to be constructed without detailed information about the underlying process. ANNs as black box modeling tools have already been used for many applications in industry, business and science [19]. Since in white box modeling approaches, the model of development is based on the information of mechanistic and relevant equations and detailed knowledge for a specific system is usually not directly available, most efforts in the white box modeling approach are devoted to revealing all relevant mechanisms and quantifying these mechanisms correctly. This usually requires an extensive research program (including experiments, which can also be very time- and money-consuming). Here a compromise must be made in order to save time and money. Therefore, white box models often have limited accuracy, because in developing the models, minor mechanisms are neglected and only the major mechanisms are taken into account. The major advantage of the artificial neural networks is that they can be constructed without the need of detailed knowledge of the underlying system. One of the applications of artificial neural network models is to map an input space to an output space and function as a look-up table. Thus, in recent years, artificial neural networks have been applied to biotechnology and biochemical engineering researches [20-27].
In this study, a Multi Layer Perceptron (MLP) neural network is utilized in order to develop an appropriate model for the prediction of products selectivity.
MLP
This type of network consists of an input layer, an output layer and one or more hidden layers (Figure 2). The number of neurons in the input and the output layer depends on the number of input and output parameters respectively. However, the hidden layer may contain desired neurons. All the layers are interconnected as shown in Figure (2) and the strength of the interconnections is determined by the weights associated with them. Each input of neurons (p) is weighted with an appropriate (w), the sum of the weighted inputs and the bias (b) forms the input to the transfer function (f). Neurons can use any differentiable transfer function f to generate their output (n) and is given as:
|
|
(7) |
Multilayer Perceptron networks often use the log-sigmoid transfer function (Eq. 8); however, other functions are commonly used.
|
|
(8) |
In this work, one hidden layer was chosen for the networks (as shown in Figure 2), and the optimum neuron numbers for hidden layer was calculated.
By using Bayesian regularization back propagation, the MLP neural network was trained. This training method updates the weight and bias values according to the Levenberg- Marquardt optimization [28]. It minimizes a combination of squared errors and weights, and then determines the correct combination so as to produce an artificial neural network that generalizes well. Training was carried out until the mean absolute relative error (MARE) which represented by Eq. 9, was minimized. When the training was terminated, to avoid over learning, the error of test and training data were calculated.
|
|
(9) |
As illustrated in Figure (2), the inputs of the proposed networks are DO value, bacteria OD and HS– load, and the outputs are elemental sulfur, sulfate and thiosulfate selectivity. To choose the best network structure, different configurations of MLP networks were trained and tested. Network parameters such as: numbers of hidden layers, numbers of neurons in each hidden layer, transfer functions and training algorithm were studied in this attempt. Eventually, the network structure that produced the smallest error for testing and training data was determined.
The needed experimental data were measured at different DO values, bacteria ODs and HS– loads, and comprise 300 observations. Using the random selection method, 75% of all data (225 data sets) were assigned to the training set, while the rest of the data were used as the validation set.
Results and Discussions
A part of the obtained experimental data are shown in Table (1). According to the results, increasing of bacteria OD leads to more sulfur and sulfate selectivity, but leads to decrease of thiosulfate selectivity. Although, by increasing DO value, sulfate and thiosulfate selectivity increase, and sulfur selectivity decreases. In addition, increasing sulfide load leads to increase of elemental sulfur and thiosulfate selectivity, and decrease in sulfate selectivity.
After many attempts, the best ANN obtained is a MLP with one hidden layer. The optimum number of neurons in the hidden layer is 15 neurons as shown in Figure (3). The transfer function of the first layers is a hyperbolic tangent sigmoid (Eq. 9) and that of second layer is a positive linear function. The parameters of the ANN structure are shown in Table (2).
As shown in Figure (4) the ANN model has been able to capture all the features of the system reasonably and can be used for estimating the product selectivity within the range in which it has been trained. Figure (4a) compares the results of applying the training data and Figure (4b) compares the applying test data to the MLP with experimental data at different conditions.
The correlation coefficient (R2) value of the ANN model is near to one, which indicates a good accuracy of the ANN model.
The relative error between experimental data and calculated values, for verification data are illustrated in Figure (5). As seen in this figure, mean absolute relative error (MARE%) for sulfate, sulfur and thiosulfate selectivity are 4.4, 1.77 and 0.23% respectively. The results show that the proposed model is in a good agreement with experimental data which ANN did not observe in the training phase.
Conclusion
In biological sulfide removal, elemental sulfur production should be maximized to save more hydroxyl ions. Thus, the prediction of product selectivity is essential in the design of the biological sulfide removal system. An artificial neural network based model was developed for the prediction of product selectivity as a function of DO, OD of bacteria and HS– load, in the biological sulfide removal system. The best architecture of the MLP network was obtained by trial. Application of the proposed ANN model for training and test data indicates that it can predict the product selectivity with a considerable accuracy.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal











