Testing Purchasing Power Parity
| ✅ Paper Type: Free Essay | ✅ Subject: Economics |
| ✅ Wordcount: 2309 words | ✅ Published: 17 Oct 2017 |
Within this paper a combination of univariate models (which assume the value of the exchange rate is based on its past values) and multivariate models (which will consider the trend in domestic and foreign prices) will be used to test the Purchasing Power Parity hypothesis. The data used will be the CPI for Japan and Sweden along with the exchange rate for the Japanese Yen and Swedish Krona. The paper will aim to find the best univariate and multivariate models and then compare their performance to the actual data.
For the univariate analysis the log of the exchange rate (et) and the respective growth rate (∆et) will be considered for the period of July 1997 – September 2013, the data for October 2013 – September 2014 will be emitted and used for testing the models.
1. Estimate appropriate ARMA models for the log of the nominal exchange e
And for the respective growth rate (∆e), carefully explaining how your models were selected.
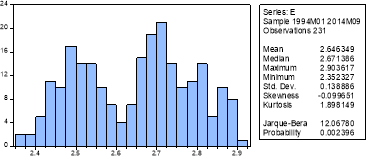

From initial inspection of the graph of et the data seems to follow a random walk but there is some evidence that it reverts to a fixed mean which could be an example of an AR(1) process with the coefficient close to 1. The histogram does not depict a normal distribution as there are a number of peaks, this is supported by the Jarque-Bera test and we can conclude we do not have a normal distribution as the P-value is insignificant at the 1% significance level and therefore we reject the null hypothesis of normally distributed errors.

From the correlogram it appears that the process is an AR(1) as the autocorrelation dies down gradually and the partial correlation dies out after 1 lag. Other models will also be tested to ascertain if there are better models available. From this testing the best model found based on the information criteria was an AR(1) AR(4) with the lags being significant at the 5% significance level. The P-value for the 4th lag in the AR(1) AR(4) model was only just below this significance level, which could suggest the AR(1) model will actually perform better when forecasting, this model was also significant at the 5% significance level and will also be used as a model with less lags may perform better and the information criteria were only slightly worse (see appendix i for a list of regression outputs and significance levels).
|
Model |
AIC |
SC |
HQ |
|||
|
AR(1) |
|
|
|
|||
|
AR(1) AR(4) |
|
|
|
It can be shown that both of these models are stationary which you would expect when comparing the exchange rates between two countries whose economies have followed a similar path.


Following the same process for ∆e for e it appears that the data is white noise with a large amount of noise around 07/08, this could be as a consequence of the recession at that time. The P-value for the Jarque-Bera test is insignificant at the 1% significance level and therefore we reject the null hypothesis of normally distributed errors. The mean is close to zero but there is negative skewness and high kurtosis.

Examining the correlogram shows no distinct signs of Autocorrelation or Partial correlation which could imply an ARMA model. Using trial and error and examining the information criteria as well as the significance of the lags; the best two models were as below, no other models were significant at the 5% significance level with respect to variables (see appendix ii for a list of regression outputs and significance levels).
|
Model |
AIC |
SC |
HQ |
|||
|
AR(1) MA(1) |
|
|
|
|||
|
Constant |
|
|
|
This suggests that an AR(1) MA(1) model is best but also that using a model which assumes that ∆et is constant will also work as a good model for the exchange rate.
2. Obtain 12-step ahead forecasts for the mean of e using both modelling approaches from 1. and assess their forecasting ability.
The forecasted values were calculated 12 steps ahead for each model and then compared to the actual results using the RMSE, MAE, MAPE and U. For the two models for et AR(1) and AR(1) AR(4) the results suggest that the AR(1) model performed better at forecasting due to the lower RMSE, MAE, MAPE and U values. The forecasts for ∆et were converted to forecasts of et so that the results were comparable.
For the two models using ∆et it can be seen that the constant model performs better as a forecast for future exchange rates between Japan and Sweden. This suggests that the exchange rate will continue to adjust at the same rate as in the last period accounted for (2013m09). We can conclude that the constant model is the best forecast method for the logged exchange rates between Japan and Sweden as all 4 indicators are smallest for this model. It is however unlikely in practice for an exchange rate to grow at a constant rate as usually exchange rates fluctuate largely as a result of shocks to the respective economies. It perhaps suggests that the other models are not largely successful at forecasting changes in the exchange rate instead of suggesting strength of the model with no allowance for past lags. This could be due to the other models over-estimating fluctuations in the exchange rates. This could be due to the presence of ARCH effects.
|
Forecast |
||||
|
Model |
RMSE |
MAE |
MAPE |
U |
|
e AR(1) AR(4) |
0.0533860 |
0.0476250 |
1.7314010 |
0.0098290 |
|
e AR(1) |
0.0439990 |
0.0368120 |
1.3360190 |
0.0080850 |
|
∆e AR(1) MA (1) |
0.0350707 |
0.0276425 |
1.0021864 |
0.0064299 |
|
∆e constant |
0.03205544 |
0.02585021 |
0.93857607 |
0.00586893 |
3. Estimate a GARCH-type model for e, carefully explaining how your preferred model was selected. Test for the presence of ARCH effects in the residuals.
For all of the 4 above models when viewing the squared residuals for each of the previously tested models it can be seen that the p values are less than 0.1 and when conducting the ARCH heteroskedacity test and examining the P-value of the chi-squared statistic the value is always close to 0 therefore for all models we reject the null hypothesis of no ARCH effects and conclude that the use of an ARCH or GARCH model is needed. As earlier mentioned et and ∆et are not normally distributed and so the t-distribution will be used.
|
Model |
P-value of chi-squared stat |
P-value squared residuals HQ |
|||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
et AR(1) AR(4) |
0.0353 |
0.002 |
0.001 |
0.000 |
0.000 |
0.001 |
0.002 |
0.003 |
0.006 |
0.008 |
0.013 |
||
|
et AR(1) |
0.0030 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.001 |
|
|
∆et constant |
0.0063 |
0.006 |
0.000 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.001 |
0.002 |
0.002 |
0.003 |
|
∆et AR(1) MA(1) |
0.0311 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.001 |
0.001 |
0.002 |
Initially the AR(1) AR(4) model for et was tested and the p-value for AR(4) was insignificant, therefore this was dropped and an AR(1) model was tested. This produced significant results for all variables and eliminated arch effects as shown by the p-values of squared residuals being greater than 0.1 and the ARCH heteroskedacity test producing a significant p-value. This model was also tested with higher order ARCH/GARCH but no better models were found as shown by the information criteria below. Therefore the AR (1) GARCH (1,1) model will be used going forward. (Full results can be seen in appendix iii).
|
Model |
AIC |
SC |
HQ |
|
AR(1) AR(4) GARCH (1,1) |
-3.659711 |
-3.54997 |
-3.61537 |
|
AR(1) GARCH (1,1) |
-3.647996 |
-3.55485 |
-3.61037 |
|
AR(1) GARCH (0,1) |
-3.629104 |
-3.55148 |
-3.59775 |
|
AR(1) ARCH (1) |
-3.625353 |
-3.54773 |
-3.594 |
|
AR(1) GARCH (2,1) |
-3.643651 |
-3.53497 |
-3.59976 |
|
AR(1) GARCH (1,2) |
-3.643243 |
-3.53457 |
-3.59935 |
The same process was used for the two models of ∆e and the information criteria suggest a AR(1) MA(1) GARCH (1,1) is best. This also removed ARCH effects as shown by the p-values of the squared residuals all being greater than 0.1 the ARCH heteroskedacity test producing a significant p-value (see appendix iv for full results). Going forward the AR(1) GARCH (1,1) for et will be used and the AR(1) MA(1) GARCH (1,1) for ∆et.
|
Model |
AIC |
SC |
HQ |
|
Constant GARCH (1,1) |
-3.648715 |
-3.57109 |
-3.61736 |
|
Constant GARCH (2,1) |
-3.646597 |
-3.55345 |
-3.60897 |
|
Constant GARCH (1,2) |
-3.64412 |
-3.55097 |
-3.6065 |
|
Constant GARCH (0,1) |
-3.627903 |
-3.5658 |
-3.60282 |
|
Constant ARCH (1) |
-3.630404 |
-3.5683 |
-3.60532 |
|
AR(1) MA(1) GARCH (1,1) |
-3.665609 |
-3.55658 |
-3.62157 |
|
AR(1) MA(1) GARCH (2,1) |
-3.665693 |
-3.54109 |
-3.61536 |
|
AR(1) MA(1) GARCH (1,2) |
-3.661519 |
-3.53691 |
-3.61118 |
|
AR(1) MA(1) GARCH (0,1) |
-3.645766 |
-3.55231 |
-3.60802 |
|
AR(1) MA(1) ARCH (1) |
-3.65517 |
-3.56172 |
-3.61742 |
4. Test if there is any evidence of:
i) a link between volatility and nominal exchange rate movements.
By running a GARCH model and altering the arch in mean to use the standard deviation or log of variance, a test for a link between volatility and nominal exchange rate movements can be conducted. If the model is significant and the information criteria improve this shows there is a link between volatility and nominal exchange rate movements. This will be tested for both the AR(1) MA(1) GARCH (1,1) for ∆et and the AR(1) GARCH (1,1) for et.
|
et AR(1) GARCH (1,1) |
||||
|
AIC |
SC |
HQ |
P-value of the regressor |
|
|
none |
-3.647996 |
-3.554845 |
-3.610371 |
– |
|
Std. dev. |
-3.638826 |
-3.530149 |
-3.594930 |
0.9758 |
|
Log (var) |
-3.639104 |
-3.530428 |
-3.595208 |
0.7914 |
|
∆et AR(1) MA(1) GARCH (1,1) |
||||
|
AIC |
SC |
HQ |
P-value of the regressor |
|
|
none |
-3.665609 |
-3.556580 |
-3.621566 |
– |
|
Std. dev. |
-3.656607 |
-3.532003 |
-3.606272 |
0.8223 |
|
Log (var) |
-3.656575 |
-3.531970 |
-3.606240 |
0.8428 |
It can be seen for the above that the information criteria do not improve for either model and likewise the p-values for the repressor’s are insignificant, therefore we conclude there is no link between volatility and nominal exchange rate movements.
ii) asymmetric volatility.
To test for asymmetric volatility the above models will be tested again using EGARCH and TGARCH models, if they are significant and the information criteria improve we can conclude there is asymmetric volatility.
|
et AR(1) GARCH (1,1) |
||||
|
AIC |
SC |
HQ |
P-value of regressor(s) |
|
|
GARCH |
-3.647996 |
-3.554845 |
-3.610371 |
– |
|
EGARCH |
-3.597413 |
-3.504261 |
-3.559788 |
0.0123, 0.0023, 0.0309 |
|
TGARCH |
-3.667624 |
-3.558948 |
-3.623728 |
0.0005, 0.0000, 0.0000 |
For the EGARCH model all of the regressors are significant however the information criteria are worse so we will discount this. For the TGARCH we can see that all of the information criteria are better and the regressors are all significant at the 5% significance level and therefore we can conclude there is evidence of asymmetric volatility and the TGARCH model should be used.
|
∆et AR(1) MA(1) GARCH (1,1) |
||||
|
AIC |
SC |
HQ |
P-value of regressor(s) |
|
|
GARCH |
-3.665609 |
-3.556580 |
-3.621566 |
– |
|
TGARCH |
-3.710058 |
-3.585453 |
-3.659723 |
0.0000, 0.0076, 0.0000 |
|
EGARCH |
-3.678623 |
-3.554019 |
-3.628288 |
0.0381, 0.7862, 0.0024, 0.0014 |
Similarly the results for the preferred model ∆e AR(1) MA(1) show evidence of asymmetric volatility and suggest that a TGARCH model should be used.
5. Given the results in above, reassess the forecasting performance of your competing models for et (12-step ahead).
|
Forecast |
||||
|
Model |
RMSE |
MAE |
MAPE |
U |
|
e AR(1) AR(4) |
0.0533860 |
0.0476250 |
1.7314010 |
0.0098290 |
|
e AR(1) |
0.0439990 |
0.0368120 |
1.3360190 |
0.0080850 |
|
∆e AR(1) MA (1) |
0.0350707 |
0.0276425 |
1.0021864 |
0.0064299 |
|
∆e constant |
0.03205544 |
0.02585021 |
0.93857607 |
0.00586893 |
|
∆e AR(1) MA(1) TGARCH |
0.032527852 |
0.026321482 |
0.955692971 |
0.005956007 |
|
e AR(1) EGARCH |
0.038058768 |
0.029901757 |
1.083818142 |
0.006983289 |
As can be seen from the above results, despite adopting new models to account for the ARCH effects and asymmetric volatility the results still suggest that a constant model is the best forecast of the exchange rate. The models accounting for ARCH effects and asymmetric volatility did however perform better than there previous equivalents. It seems that using a constant estimator is the best forecast of exchange rates for the 12 month period however if looking further in to the future it would seem unlikely this would be the case as exchange rates fluctuate over time. If modelling further in to the future the model of choice would be the ∆e AR(1) MA(1) TGARCH.
6. Using the to your case, study (and test for) Granger-causality among exchange rates and prices.
The variables Pt (log(cpi_japan_sa)) and Pft (log(cpi_sweden_sa)) were created in order to conduct the multivariate analysis and test the Purchasing Power Parity hypothesis (et = pt – pft + ut). Initially a VAR model with endogenous variables et, Pt and Pft was estimated with an adjustedsample period to 2012m08 (to remove 12 periods for sampling). By inspecting the lag length criteria for 12 lags (due to the monthly data) it can be seen that 2 lags should be used as 3/5 information criteria suggest this with 1 other suggesting 1 lag and the other 10 lags.
|
Lag |
LogL |
LR |
FPE |
AIC |
SC |
HQ |
|
0 |
1058.334 |
NA |
3.78e-09 |
-10.87973 |
-10.82919 |
-10.85927 |
|
1 |
2173.030 |
2183.427 |
4.24e-14 |
-22.27866 |
-22.07653* |
-22.19681 |
|
2 |
2188.028 |
28.91262 |
3.98e-14* |
-22.34049* |
-21.98676 |
-22.19726* |
|
3 |
2191.883 |
7.312518 |
4.20e-14 |
-22.28745 |
-21.78211 |
-22.08283 |
|
4 |
2201.900 |
18.69171 |
4.16e-14 |
-22.29794 |
-21.64100 |
-22.03192 |
|
5 |
2203.370 |
2.697145 |
4.50e-14 |
-22.22031 |
-21.41176 |
-21.89290 |
|
6 |
2208.951 |
10.06880 |
4.66e-14 |
-22.18506 |
-21.22492 |
-21.79627 |
|
7 |
2213.684 |
8.392441 |
4.88e-14 |
-22.14107 |
-21.02932 |
-21.69089 |
|
8 |
2216.622 |
5.118809 |
5.20e-14 |
-22.07857 |
-20.81523 |
-21.56701 |
|
9 |
2222.562 |
10.16563 |
5.37e-14 |
-22.04703 |
-20.63208 |
-21.47408 |
|
10 |
2232.998 |
17.53626* |
5.31e-14 |
-22.06183 |
-20.49528 |
-21.42749 |
|
11 |
2238.369 |
8.860814 |
5.52e-14 |
-22.02443 |
-20.30627 |
-21.32870 |
|
12 |
2245.094 |
10.88415 |
5.67e-14 |
-22.00097 |
-20.13122 |
-21.24385 |
The Granger Causality test was then conducted. From this it can be seen that at the 5% significance level we can reject the null of no causality from Pft to Pt and that we can reject the null of no causality from et and Pft collectively to Pt. This is not a result you would expect to occur intuitively as it would not be expected that a change in Pt would be as a consequence of a change in Pft.
|
Dependent variable: E |
|||
|
Excluded |
Chi-sq |
df |
Prob. |
|
PT |
3.138309 |
2 |
0.2082 |
|
PFT |
0.087914 |
2 |
0.957 |
|
All |
4.648441 |
4 |
0.3253 |
|
Dependent variable: PT |
|||
|
Excluded |
Chi-sq |
df |
Prob. |
|
E |
5.63532 |
2 |
0.0597 |
|
PFT |
13.94933 |
2 |
0.0009 |
|
All |
15.13495 |
4 |
0.0044 |
|
Dependent variable: PFT |
|||
|
Excluded |
Chi-sq |
df |
Prob. |
|
E |
0.175002 |
2 |
0.9162 |
|
PT |
2.819637 |
2 |
0.2442 |
|
All |
4.540737 |
4 |
0.3377 |
For the rest of the variables we fail to reject the null at the 5% significance level and therefore conclude there is no causality. This is not supporting of the PPP hypothesis in which you would expect to conclude causality from Pft and Pt to et.
7. Test whether or not et, pt and pft are stationary (several methods are possible, here).
The first step before testing for stationarity using the augmented Dickey-Fuller test is to inspect the graphs of the variables to establish if they have a trend and/or an intercept. It can be seen for the graphs of et and pt that both have an intercept as they fluctuate around a non-zero mean, however neither appear to have a very obvious trend. Therefore when conducting the test only allowance for an intercept will be used but nothing for trend. From the graph of pft we can see that there is an intercept and that there is a clear upward trend therefore an allowance for intercept and for trend will be used. (see appendix ?? for graphs)
From conducting the ADF test and examining the p-values we fail to reject the null hypothesis that the series has a unit root and therefore is non-stationary at the 5% significance level for all of the variables (et, pt and pft). In other words there is insufficient evidence to suggest that they are stationary.
|
Augmented Dickey-Fuller Test Results |
|
|
Variable |
Prob. |
|
et |
0.1411 |
|
pt |
0.6134 |
|
pft |
0.7305 |
|
∆et |
0.0000 |
|
∆pt |
0.0000 |
|
∆pft |
0.0000 |
For each of the v
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


