Monotonic Transformation of Utility Function

WHY TAKING A MONOTONIC TRANSFORMATION OF A UTILITY FUNCTION DOES NOT CHANGE THE MARGINAL RATE OF SUBSTITUTION

Utility is the ability to satisfy certain wants and needs. It is considered an essential concept in economics because, it shows the satisfaction received from the consumption of a good or service, and it also considered to be a method of assigning a number to every consumption bundle, such that more preferred bundles get assigned larger numbers than less preferred bundles, in essence economist recognize that it can not be measured, it is impossible to directly measure the pleasure or satisfaction from the consumption of a good or service, because of that economist came up with ways of representing measuring utility in terms of economic choices that can be counted, utility is considered to be revealed in people’s willingness to pay for different amount for different goods.

We have different types of utility functions, the cardinal utility function, the ordinal utility function, expected utility function etc.

The cardinal utility function argues that a consumer has the ability to measure the level of utility he/she derives from the consumption of a given quantity of goods, cardinal utility is the term associated with the uniqueness of a utility function up to increasing linear transformation, and is related among other things, to the ranking of utility differences.

It plays a major role in many branches of current economic analysis, such as the theory of social welfare, the theory of intertemporal decisions and the theory of decision under risk.

The main assumptions of the cardinal utility are: rationality, it assumes that the consumer is rational, diminishing marginal utility: it assumes that the marginal utility obtained from the consumption of a commodity diminishes continuously as its consumption is increased, another assumption of the cardinal utility is the introspection method, for example as the more and more of a good an individual purchases the less utility derived from the additional units of it.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

The cardinalist school assumes the behavior of marginal utility in the mind of another person can be showed with the help of self observation, the cardinal utility has its criticisms by an Italian economist known as Poreto,he seriously criticized the concept of cardinal utility, he stated that utility is not quantifiable or oddible; it can however be compared, he suggested that the concept of utility should be replaced by the scale preference.

The cardinal utility approach is replaced by ordinal utility function.

The ordinal utility function theory, states that a utility of a commodity or service cannot be measured using a numerical scale bearing economic meaning in an of pairs of alternative combinations of commodities can be ordered such that one is considered by an individual to be equal to, worse than or better than the order, this is in contrast with cardinal utility theory which treats utility as something whose numerical value is meaningful in its own right, ordinal utility assumes that it is not possible to measure or express the utility of a consumer of a product in qualitative terms, but it is always possible for the consumer to tell which of any two goods they and also consumer can list all the product they consume in the order of their preference for the goods, this gives the essence of ordinal utility.

The utility of a consumer can be measured using an indifference curve, which is the locus of points each representing a different combination of two goods giving the same level of satisfaction or utility to a consumer, therefore a consumer is indifferent between any two combinations of goods when it comes to making a choice between them, a situation like this arises because a consumer consumes a large amount of goods and services and often finds out that one products serves as a substitute for the another, when such combinations are plotted graphically it results in a curve , known as the indifference curve(as mentioned earlier) or equal utility curves.

The concept of marginal rate of substitution (MRS) is the level or rate at which one product or commodity can be substituted or exchanged for another and the level of satisfaction stays unchanged.

In order to explain the concept of marginal rate of substitution (MRS), assume that a consumer consumes only two goods X and Y and the utility function of the product for the consumer is given as;

U=F (X, Y)

Where x and y are imperfect substitutes, suppose the consumer now substitutes x for y such that the total utility remains unchanged when the consumer gives up some components of Y, the stock of Y decreases by change in Y and the consumer loses a part of the total utility of the commodity, the loss of utility may be expressed as 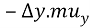, as a result of substitution the stock of x increases by , the corresponding gain of utility from equals

–= +

The total utility remains unchanged, or the same only when

=

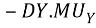So basically, the amount of a product that a consumer is willing to sacrifice for another as long as the level of satisfaction is the same, is known as marginal rate of substitution, and it is calculated using

MRS =

Monotonic transformation is a way of transforming a set of numbers into another set that preserves the order of the original set, it is a function mapping real numbers into real numbers, which satisfies the property, that if x>y, then f(x)>f(y), simply it is a strictly increasing function.

Applying a monotonic transformation to a utility function representing a preference relation simply creates another utility function representing the same preference utility of utility, basically what this means is that when monotonic transformation of utility is applied the marginal rate of substitution does not change here is why.

Marginal rate of substitution does not change when a transformation of utility function is undertaking by any positive monotonic transformation, this will be presented through a concept, by an example

U (X, Y)=X^0.4 Y^0.6

Computing marginal rate of substitution

For U (X) and U (Y), marginal rate of substitution is the

Ration of marginal utility.

MRS=UxUy

Computing for marginal derivative

=0.4() ^0.6

0.6() ^0.4

=

V (X, Y)=2 LOGx +3 LOGv

MRS=

Computing for marginal utilities

MRS= =

Simplification

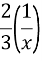
So basically the expression of the marginal rate of substitution is equal to the second function, different utility functions can give you the exact same preference, the two functions can be related to express one as the function of the other;

V (x,y) = LOGx² +LOGv³

=LOG (x² y3) = LOG ((x²⁵ y^3|5)) =

LOG ((v (x, y5))

V (X, Y)= 5 LOG (U(X,Y))

These two utility functions are directly related to one another and not only are they directly related but if the derivative of (5 log(v(x,y)), is being applied to the utility function of

U (x, y)=x^0.4 y^0.6 , a positive derivative will be obtained, this is why generally it is the case consider a general argument for why , the marginal rate of substitution *************** $$$$$$$$$, where the same for the utility function of V(X,Y) U(X,Y)

V (x, y)=g(u(x,y)), suppose there is a utility function of U(x,y), it is then transformed by applying an increasing function G,G has a positive derivative no matter what value it is applied in this =g(U(x,y)), and the result is this new utility function of V (x,y), given this setup the marginal rate of substitution for this V(x,y) =

MRS=VxVy

here the marginal utility can be computed simply by taking the derivative of the outside function(g(u(x,y))) and multiply it by the derivative of the inside function

MRS=VxVy=g¹(u(x,y)) .Ux g¹(u(x,y)) .Ux

this is an expression of the marginal rate of substitution using the utility function V(X,Y)

MRS=VxVy=g¹(u (x,y)) .Ux g¹(u(x,y)) .Ux(This derivative can be cancelled out as long as they are positive)

Which means it can be divided through by g¹ which will be

MRS=VxVy=g¹(u (x,y)) .Ux g¹(u(x,y)) .Ux= UxUy

The marginal rate of substitution are the same for the utility function U(x,y) and any increasing transformation of u(X,Y), so if the utilities are to be transformed to some other utility function using some increasing function , the marginal rate of substitution will not be changed because the marginal rate of substitution will not be changed at any point , the preferences that where describing using transformed utility function are no different , so when we have this transformation of cobb Douglass utility function

=V (x, y)= 5 log (u(x,y)

Transforming it by log and multiplying it by 5that did not change what was computed for the marginal rate of substitution.

Subtracting or adding a number of “units” from a utility function does not change the ordering of the preferences. It makes the utility level shift up or down by some constant number of units. Multiplying a utility function by any positive number is also simple. This change multiplies the number of units of utility by that positive number without changing their order. The same goes for exponents as long as the application of the same positive exponent is done to the whole utility function, we just increase or decrease the number of units by that exponent with- out changing the order.

“the preference and indifference curve order remains the same with a positive monotonic transformation of utility function this is true for any monotonic transformation including multiplying a utility function by a positive constant or raising the function to the power of some positive constant”[1]

All this is basically a demonstration of why a monotonic transformation of a utility function does not affect or change the marginal rate of substitution.

[1] Microeconomic theory: concepts connections by Michael Eugene Wetzstein