Effect of Competition of on Social Preferences in Bargaining

Does competition affect social preferences in a bargaining game?

Since the first day learning economics, we all remember the most basic presumption of classical economic theory that individuals’ decision making are entirely driven by their material self-interest and there is nothing related to “social goals”. Many pieces of evidence have proved that it is true for some people in some circumstances, but not represent the whole human kind. Adam Smith, the father of “The Invisible Hand”, did write these lines in his book, “The Theory of Moral Sentiments”:

“How selfish soever man may be supposed, there are evidently some principles in his nature, which interest him in the fortune of others, and render their happiness necessary to him, though he derives nothing from it except the pleasure of seeing it”

(Smith, 1759)

Are people really that selfish or they are actually fair-minded and cooperative in the end? Why do we trust in each other and why we still contribute ourselves and engage in community work? Reality has shown that actually, we also care about the fairness and people are more cooperative than is assumed in self-interest model. Social preferences, which is “how people rank different allocations to themselves and others” (Drouvelis, 2013), have a significant impact in decision-making process of agents in a number of economic settings, like charity, community work and bargaining. Thus, studying on social preferences and how they interact with material incentives will help improve the ability to predict behaviour as well as make policy recommendations. This paper will summarize several empirical experiments to find out how competition affect social preferences in the framework of a bargaining game: ultimatum game.

Bargaining is a kind of negotiation, which normally occurs when there is a trade, in which the buyer and seller debate the price and the basic nature of that transaction. Bargaining is a frequent part of our daily life, when an employee bargains for a higher salary, or when the owners of a company negotiate with his striking workers. At the end of the bargaining process, one party makes a “take it or leave it” offer. If that ultimatum offer is accepted, then it leads to a resolution. Otherwise, sometimes both sides have to suffer substantial financial losses. Under the limited scope of this essay, we will only look at the simplified version of the ultimatum game.

In this game, players will be divided into proposers and responders (receivers) and then bargain about the distribution of a fixed amount of money. Firstly, the proposer has to offer a share of the initial surplus to the responder. After considering if the share is fair enough, the responder can accept or reject. In case of acceptance, the receiver will receive the offered amount and the proposer will receive the remaining part of the initial amount. In case of a rejection, both players receive nothing.

In 1982, the first experimental test of the “ultimatum game” had been conducted by Guth, Schmittberger and Schwarze, three economists at the University of Cologne, who were studying bargaining behaviour. Back then, Guth and his colleagues recruited a group of graduate students and group them up to form 21 pairs. The proposer was given a fixed sum S of money and he had to announce a split of that amount between himself and a responder .After considering if the offer x is fair enough, the responder can accept or reject. In case of acceptance, the receiver will receive the offered amount x and the proposer will receive the remaining part S-x of the initial amount. In case of a rejection, both players receive nothing. At the first sight, the game was expected to be easy if all of the responders only care about their material outcomes, they will be willing to accept any positive offer and the proposer will offer the minimum amount to get the most. It also means that there will be a unique Nash equilibrium when the proposer offers nearly zero and the responder still accept. However, it turned out not to happen that way. One-third of the proposers offered exactly half of the initial amount responder and more than 80% of them offered the responder at least 20% or more of the amount available. 10% of the offers were rejected. This result is very surprising as the proposers offer more than they have to while in one particular case where the responder was offered 20% but still rejected. Surprised and intrigued, Guth and his colleagues decided to carry out the experiment again but observed behaviours still illustrated a significant deviation from the equilibrium.

Reporting the results, Guth et al commented: “The main reason seems to be that the rational solution is not considered as socially acceptable or fair”. Chaudhuri (2008) reported that for further studying, Guth and his colleagues asked the students to participate in other much more complex versions of the game but the outcomes was very consistent, even when Camerer tried again in a different country in 2003. These results vigorously proved that not the inability to understand the game but their idea of a fair offer that matters, and indeed it can be explained by so called “social preferences”. It indicates that people are not primarily interested in maximizing their monetary payoffs in particular or his utility in general, they also pay a lot of their attention to other social norms like fairness or inequity-aversion. In other words, people tend to resist inequitable outcomes and they are willing to turn down the offer even in “at a cost to themselves” to move in the direction of a more equitable one. (Wilkinson,2008).

In an attempt to dig deeper in the competition in the ultimatum game, Roth et al (1991) carried out the experiments and observed variation between bargaining data and market data across four different locations – Pittsburgh, Ljubljana (Slovenia), Tokyo and Jerusalem. Proposers in each country were asked to split 1000 tokens, which will be converted to real money at the end of session. But now, there will be two games: the classic ultimatum games and the “multi person market behaviour” game. In the second game, proposers have to compete each other: there is n-1 proposers (n participants) who concurrently propose an offer to responder. Needless to mention, the responder has the opportunity to consider the highest offer. If there are more than one proposers offer the highest offer, one of them is randomly selected. Once again, if self-interest hypothesis was observed, in the classic ultimatum game, the proposers were expected to virtually get all gains from trade while in the market game, the situation will be reversed and the responder will get the most out of 1000 tokens. Knowing that the responder will only accept the highest offer, proposer knew that he would earn no return if his offer is less than the others. Therefore, all of the splits will be raised up as high as possible, as long as he still earn something which was considered to be fair. Theoretically, there will be a unique sub-game perfect equilibrium outcome when at least two proposers make an offer of all tokens and then the responder gets all from the trade.

Different modes of games bring back different kind of results. The first game reflects the differences in the social norm “fairness” of each society while the second was meant to test whether the story will be different when the responders have more market power. The data collected from experiment in bargaining environment was consistent with the classic game, when it deviated strictly from the perfect equilibrium and proposals are much nearer the middle of the range. In the market environment, the outcomes were observed to converge quickly to the Nash equilibrium and do not deviate once it has been achieved.

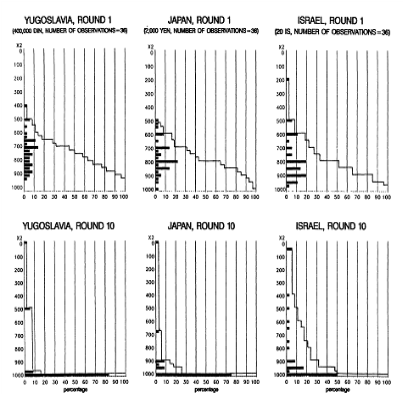
Figure 1: Game with proposer competition – Market Data

Source: Roth et al (1991:1080-1081)

From the figure 1, we can see that after few periods, all four markets in four countries reached to the sub perfect equilibrium and stay there after that. People try different strategies in the early rounds and then quickly come to the same solution to offer nearly all of the tokens to the responders. For example, in Japan case, market outcome changed significantly from about 40% proposers offered lower than 800 tokens in round 1 to nearly 5% who offered that amount in round 10. The same situation can also be observed in Yugoslavia, Israel and US. In other words, the empirical results are quite consistent with the data from the standard ultimatum game.

The ultimatum game issue didn’t stop here as our economists wanted to study more about the effect of competition on social preferences. Fischbacher et al. (2009) introduced three treatments to the participants to assess the impacts of competitions on the responders’ side. The first treatment was similar to the standard two-player ultimatum game (BG). The second treatment (RC2) added one more responder into the game and the number of responders in the third treatment (RC5) is five. In these treatments, the structure of the game are quite similar to the standard ultimatum game except that there is more than one responders in RC2 and RC5. Now, the proposers were asked to divide their 100 units of money to the responders and the responders have to make the decisions without knowing the choices of others. In the event that all responders reject, all participants earn zero. The prediction about the outcome of these treatments with purely selfish preferences is straightforward and all responders are expected to accept any offer with a positive amount. Once again, there would be a subgame perfect equilibrium outcome when the proposer offer zero and that is still accepted by at least one responder. In the end, the game progressed in the same way as it did in 1982 in Guth’s experiment. Figure 2 will provide us a glimpse over the results of all three treatments.

Figure 2: Game with responders’ competition

(Source: Fishbacher et al, 2009:535)

We can see that the acceptance thresholds of responders keeps decreasing further and further as the game progress. As we introduce more responders into the game, they will be more resisted to reject the offers which used to be low with the fear that other responders will take it. In the graph, the average accepted offers in RC2 and RC5 are quite similar but if we compare to the situation in BG, there would be a huge difference. To summarize, both the introduction of the competition and the increase in responder reduced the accepted amount considerably.

In a nutshell, from the ultimatum game, fairness concerns play a big role in our process of decision making. In the standard ultimatum game, some are willing to give up some kind of profit when they feel that they are being treated unfairly. However, it is ambiguous to define that feeling of “unfairness”. In some circumstances, to be fair or unfair is related to the relative payoffs, when the responders did not hesitate to turn down the low offers in the standard ultimatum games. In other cases, the social norms “fairness”, like other non-monetary concerns, is completely dominated by the competition effects. Like in the games with proposers and responders’ competition, when participants know that the inequality outcomes are unavoidable, they try their best to turn that equality into advantage and to increase their monetary payoffs as much as possible. At the end of the day, competition force people to be selfish.

References

1. Smith, 1759: ‘The Theory of Moral Sentiments’
2. Chaudhuri, A. (2008) ‘Experiments in economics: playing fair with money’. New York: Routledge
3. Drouvelis, M. (2013) ‘Application of prospect theory and social preferences’.
4. Roth, A.E., Prasnikar, V., Fujiwara, M.O & Zamir, S. (1991), ‘Bargaining and Market Behavior in Jerusalem, Ljubljana, Pittsburgh and Tokyo: An Experimental Study’ The American Economic Review 81 (5) 1068-1095
5. Fischbacher, U., Fong, C.M. & Fehr, E. (2009) ‘Fairness, errors and the power of competition’, Journal of Economic Behavior & Organization 72 (2009) 527-545
6. Camerer, C.F., Loewenstein,G. & Rabin, M. (2004) ‘Advances in Behavioural Economics’, Russel Sage Foundation, New York
7. Wilkinson, N. (2008) ‘An introduction to behavioural economics.’ Basingstoke: Palgrave Macmillan