Country Comparison of Prices: Rice and Cocoa

Surname: KAREKLA

Name: MARIA

Subject 1:

1. As noted by Thompson (2001) absolute advantage occurs when a good is produced with the lower labor input per unit and comparative advantage “when relatively less of other goods must be sacrificed to produce a unit of the specialized good”⁽¹⁾. So, in this case, the amount of labor requirements per unit of output are:

So, Norway has an absolute advantage in producing both products, since its labor requirements are lower both in rice, 1<3/2, and in cocoa, 1/3<3/2.

Furthermore, in the following table

it is shown that for Norway the opportunity cost for producing 1 ton of rice is 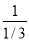=3 tons of cocoa and the opportunity cost for producing 1 ton of cocoa is =1/3 tons of rice. In Argentina, the opportunity cost for producing 1 ton of rice is =1 ton of cocoa and the opportunity cost of producing 1 ton of cocoa is =1 ton of rice. So, Norway has a comparative advantage in producing cocoa, since it has a lower opportunity cost in producing it (1/3<1) and Argentina has a comparative advantage in producing rice, having a lower opportunity cost in producing it, since 1<3.

b) In autarky the Production Possibility Frontier (PPF) is the same with the Consumption Possibility Frontier⁽²⁾. So, henceforth, L_N and L_A is the labor endowment in Norway and Argentina respectively, a^N_LR, a^N_LC and a^A_LR, a^A_LC is the amount of labor per unit of rice and cocoa in Norway and Argentina respectively, R and C is the quantity of rice and cocoa respectively⁽³⁾.

In Norway the PPF is:

L_N=a^N_LR·R+a^N_LC·C

130=1·R+1/3·C

It takes 1 worker to produce a unit of rice and 1/3 to produce a unit of cocoa. As noted by Thompson (2001) employment in rice production plus employment in cocoa production sums the labor force of Norway⁽³⁾.

If 0 cocoa is produced: 130=(1·R)+(1/3·0)

R=130/1=130

If 0 rice is produced: 130=(1·0)+(1/3·C)

C==390

So, the autarky PPF,CPF diagram of Norway is as follows:

As noted by Thompson (2001) Norway produces at the two endpoints of the PPF, (130,0) or (0,390) or at any other point between them⁽³⁾.

In the same way, in Argentina the PPF is:

L_A=a^A_LR·R+ a^A_LC·C

390=(3/2·R)+(3/2·C)

If 0 cocoa is produced: 390=(3/2·R)+(3/2·0)

R==260

If 0 rice is produced: 390=(3/2·0)+(3/2·C)

C==260

So, the autarky PPF,CPF diagram of Argentina is as follows:

Furthermore, the relative price of rice in Norway is 3 and of cocoa is 1/3, the opportunity cost of one relative to the other. The relative price of rice and cocoa in Argentina is 1 for each one of them. So, in autarky cocoa is relatively cheaper in Norway, since 1/3<1, and rice is relatively cheaper in Argentina, since 3>1. Consequently, as noted by Agiomirgianakis, and Vlassis (2005) the international relative price of rice will be between 1 and 3. If it’s above 3 both countries produce rice. If it’s below 1, both countries produce cocoa. Since the international relative price of rice is 3/2, between 3 and 1, Argentina specializes in rice, producing 390.000.000×1=390.000.000 tons of rice, and Norway in cocoa, producing 130.000.000×3=390.000.000 tons of cocoa⁽⁴⁾.

Continuing, in free trade and since the world equilibrium price of rice is P_r/P_c=3/2.

This is the Norway’s new Consumption Possibility Frontier⁽⁵⁾:

P_r·q_r+P_c·q_c=P_c·390

(P_r·q_r+P_c·q_c)/P_c=390

(P_r·q_r/P_c)+(P_c·q_c/P_c)=390

[(P_r /P_c)·q_r]+q_c=390

q_c=390-[(P_r /P_c)·q_r] and since P_r/P_c=3/2 (the world equilibrium relative price of rice)

q_c=390-(3/2·q_r)

The slope of the free trade CPF is -3/2 and the diagram as follows:

This is the Argentina’s new Consumption Possibility Frontier⁽⁵⁾:

P_r·q_r+P_c·q_c=P_r·260

(P_r·q_r+P_c·q_c)/P_r=260

(P_r·q_r/P_r)+(P_c·q_c/P_r)=260

[(P_c /P_r)·q_c]+q_r=260

q_r=260-[(P_c /P_r)·q_c] and since P_r/P_c=3/2 and P_c/P_r=2/3

q_r=260-(2/3·q_c)

The slope of the free trade CPF is -2/3 and the diagram as follows:

As noted by Karagiannis, Katranidis, Palivos and Stoforos (2014) under free trade both countries can “consume combinations of the two goods that are not produced within the country”⁽⁵⁾.

c) As noted Karagiannis, Katranidis, Palivos and Stoforos (2014) the wage rates in Argentina can be calculated by W_A=P_r/a^A_LR and the wage rates in Norway by W_N=P_c/a^N_LC. So, the wage in Argentina relative to wage in Norway can be calculated as W_A/W_N=(P_r/P_c)x(a^N_LC/a^A_LR)=3/2x=x==1/2.⁽⁶⁾ So, the wages in Argentina are the ½ (half) of the wages of Norway and Argentinian workers would want to immigrate to Norway. Furthermore, as noted by Agiomirgianakis, and Vlassis (2005) one of the factors that affect the wage rates of the countries is the terms of trade, which is actually the world equilibrium price of the traded goods⁽⁷⁾.

d) As explained by Thompson (2001)⁽⁸⁾ when a country opens to free trade and due to comparative advantage specializes in one good, importing another, the domestic firms that produced this other product in autarky but at higher prices than the world price, would have reasons to object to free international trade, since they would go out of business. Their stockholders and investors would strongly oppose to such an opening to free trade since they would lose their money. Also, a lot of specialized workers would also object to free international trade since they would have to retrain to find a job in the firms of the good their country specializes from now on. However, even though the cost of retraining workers and reforming the firms to the new specialised market will be considerable, it will also be temporary and the economy, after a small transition period, will readjust to the new conditions and in long term the gains from free trade will prevail. The producers will see their market and income increase and consumers will enjoy more cheaper goods.

SUBJECT 2⁽⁹⁾:

a) In autarky the equilibrium price and quantity is where the supply and demand curve intersect, where Q_s=Q_d.

So, Q_s=Q_d

2P=600-P

2P+P=600

3P=600

P=600/3=200 € is the autarky equilibrium price.

Having found the price, we can find the equilibrium quantity: Q_d=Q_s=2P=2×200=400

b) On free trade the world price is P_w=125, the quantity supplied (Q_Sw) and demanded (Q_Dw) in the country is:

Q_Dw=600-P=600-125=475

Q_Sw=2P=2×125=250

The country’s quantity demanded of steel is 475, which is less than the quantity supplied (250), and consequently there will be Q_Dw-Q_Sw=475-250=225 imports.

c) Tariff=T and price under the tariff is the world price plus the tariff: P₂=P_w+T

So, the new quantities supplied(Qs2) and demanded(Qd2) are:

The amount that the government wants to raise, 3,750 Euros, equals the tariff times the imports⁽¹⁰⁾, which are the quantity demanded(Q_d2) minus the quantity supplied(Q_s2),

3,750=T x (Q_d2-Q_s2)

So, T=3,750/(Q_d2-Q_s2)

T=3,750/[(475-T)-(250+2T)]

T=3,750/(225-3T)

T x (225-3T)=3,750

-3T²+225T-3,750=0

[With Δ=225²-(4·-3·-3,750)=50,625-45,000=5,625 and since it is positive:]

T₁=(-225-) /(2x-3)= -300/-6=50

T₂=(-225+) /(2x-3)= -150/-6=25

So, the government can raise 3,750 € by imposing a tariff on imports of either T₁=50 or T₂=25. Which one the government should choose depends on the consumers and producers gains and losses and the net effect of each tariff, relative to which part its politicians wants to protect the most.

So, for tariff T₁: The new price is P_T1=P_W+T₁=125+50=175 and the quantity supplied and demanded is: Q_ST1=2P_T1=2×175=350, Q_DT1=600-P_T1=600-175=425.

So, the change in consumer surplus is the difference between consumer surplus with the tariff minus the consumer surplus on free trade and can be seen on the diagram as -(a+b+c+d) areas⁽⁹⁾.

So,{[(600-175)x425]/2}-{[(600-125)x475]/2}=90,312.50-112,812.50= -22,500 € the money consumers lose due to the tariff.

The change in producers surplus is the difference between producers surplus with the tariff minus producers surplus on free trade and can be seen on the diagram as the scheme a⁽⁹⁾.

[(P_T1-P_W)·Q_ST1]–([(P_T1-P_W)·(Q_ST1-Q_SW)]/2}=[(175-125)x350]-{[(175-125)x(350-250)]/2}=17,500-2,500=15,000 € the producers gain.

The net effect of tariff T₁=50 can be seen on the scheme by the two triangles b and d and is calculated as –(b+d), being actually the deadweight loss for society⁽⁹⁾:

-(b+d)= -{{[(Q_ST1-Qs_W)xT₁]/2}+{[(Q_DW-Q_DT1)xT₁]/2}}= -{{[(350-250)x50]/2}+{[(475-425)x50]/2}}=-(2,500+1,250)= -3,750 € the net effect.

So, for tariff T₂: The new price is P_T2=P_W+T₂=125+25=150 and the quantity supplied and demanded is: Q_ST2=2P_T2=2×150=300, Q_DT2=600-P_T2=600-150=450.

So, the change in consumer surplus is, as can be seen on the diagram, -(a+b+c+d) ⁽⁹⁾.

So,{[(600-150)x450]/2}-{[(600-125)x475]/2}=101,250-112,812.50= -11,562.50 € the money consumers lose due to the tariff.

The change in producers surplus is the difference between producers surplus with the tariff minus producers surplus on free trade and can be seen on the diagram as the scheme a⁽⁹⁾.

[(P_T2-P_W)·Q_ST2]–([(P_T2-P_W)·(Q_ST2-Q_SW)]/2}=[(150-125)x300]-{[(150-125)x(300-250)]/2}=7,500-625 =6,875 € the producers gain.

The net effect of tariff T2=2 is as before –(b+d) ⁽⁹⁾:

-(b+d)= -{{[(Q_ST2-Q_SW)xT₂]/2}+{[(Q_DW-Q_DT2)xT₂]/2}}= -{{[(300-250)x25]/2}+{[(475-450)x25]/2}}=-(625+312.50)= -937.50 € the net effect.

Consequently, if the government wants to protect the consumers more than the producers, it should impose tariff T₂=25 since consumers will lose less and the net effect is smaller, but if it prefers to protect producers it should impose tariff T₁=50 since they gain more with it (15,000>6,875), even though the net effect is bigger.

d) As noted by Thompson (2001) “a quota is a quantitative restriction on the level of imports”⁽¹⁰⁾. So the quota is the difference between the quantity demanded and the quantity supplied under new price. Quota =Q_Dq-Q_Sq and the new price under the quota is the world price plus q: Pq=P_w+q

So the new quantities supplied and demanded are:

The amount that the government wants to raise, 3,750 €, equals q (the price raise due to the quota) times the imports [the quantity demanded (Q_Dq) minus the quantity supplied (Q_Sq)],

3,750=q·(Q_Dq-Q_Sq)

So q=3,750/(Q_Dq-Q_Sq)

q=3,750/[(475-q)-(250+2q)]

q=3,750/(225-3q)

q·(225-3q)=3,750

-3q²+225q-3,750=0

[With Δ=225²-(4·-3·-3,750)=50,625-45,000=5,625 and since it is positive:]

q₁=(-225-) /(2x-3)= -300/-6=50

q₂=(-225+) /(2x-3)= -150/-6=25

With q₁=50, P_q1=125+50=175, and Q_Sq1=2P_q1=2×175=350, Q_Dq1=600-P_q1=600-175=425 and so the Quota=Q_Dq1-Q_Sq1=425-350=75

With q₂=25, P_q2=125+25=150, and Q_Sq2=2P_q2=2×150=300, Q_Dq2=600-P_q2=600-150=450 and so the Quota=Q_Dq2-Q_Sq2=450-300=150

As in the previous answer (c), the government can choose between a quota of 75 and 150 imports, with the same result for its income. If the government wants to protect its consumers, it will impose a quota of 150 imports since it will set a smaller price than with a quota of 75 imports (150<175) and consumers will consume more products 450>425. But if the government wants to protect producers it will impose a quota of 75 imports, since with it the producers sell more (350>300) and gain more (350×175=61250 > 45000=300×150)].

Subject 3: a) In autarky the equilibrium price (P) and quantity (Q) can be found setting quantity supplied and demanded equal:

Q_D=Q_S

180-30P=20+10P

180-20=30P+10P

160=40P

160/40=P

Since P=4, quantity is Q=Q_D=Q_S=20+10P=20+(10×4)=60

On free trade price=P_w=2 and the quantities supplied(Q_Sw) and demanded(Q_Dw) are:

Q_Dw=180-30P_w=180-(30×2)=120

Q_Sw=20+10P_w=20+(10×2)=40

The export subsidy would put the price P_s=P_W+2.5=2+2.5=4.5 € and the quantities supplied and demanded:

Q_Ds=180-30P_s=180-(30×4.5)=45

Q_Ss=20+10P_s=20+(10×4.5)=65

On free trade 40 units are supplied but 120 units are demanded, so (120-40=) 80 units are imported. The price is the world price, 2 €. With the export subsidy 65 units are supplied but only 45 are demanded in the country, so (65-45=) 20 units are exported. The new price is 4.5 €. Consumers consume less units that are more expensive.

The consumers lose from the export subsidy and their income decrease can be calculated by ΔCS= -(a+b+e+f+g) areas of the diagram⁽¹¹⁾:

a+e=(P_S-P_W)xQ_DS=(4.5-2)x45=112.5

b+f+g=[(P_S-P_W)x(Q_Dw-Q_Ds)]/2=[(4.5-2)x(120-45)]/2=187/2=93.75

So, -(a+b+e+f+g)= -(112.5+93.75)= -206.25 €

Producers gain from the export subsidy. On free trade they sell 40 units for only 2 €, but with the export subsidy they sell 65 units, (65-40=) 25 units more, for 4.5 €. The producers gain (income increase) can be calculated by ΔPS=a+b+c areas on the diagram⁽¹¹⁾:

[(P_S-P_W)xQ_Ss]–{[(Q_Ss-Q_SW)x(P_S-P_W)]/2}=[(4.5-2)x65]-{[(65-40)x(4.5-2)]/2}=162.5-31.25=131.25 €

The government loses from the export subsidy. Its loss is the budget effect and can be calculated by –(b+c+d+f) areas of the diagram⁽¹¹⁾: –(b+c+d+f)= -[(P_S-P_W)x(Q_Ss-Q_Ds)]= -[(4.5-2)x(65-45)]= -50 €.

The net effect, the deadweight loss of society, can be calculated by adding consumers lose+producers gain+budget effect= -206.25+131.25-50= -125 €

b) With the production subsidy the producers gain 2 (the world price) +2.5 (the subsidy)=4.5 € per unit of output, which is the new price (P_S) for them only⁽¹²⁾. Consumers buy still at 2 €. The new quantity produced with the new price is Q_s=20+10P=20+(10×4.5)=20+45=65. The quantity demanded didn’t change(120), so if there in no imports prohibition, consumers buy 65 from the country’s producers and (120-65=)55 are imported, all for 2€. So, consumers have no gains or loss from the production subsidy⁽¹²⁾.

The government loses the amount of the subsidy: 65unitsX2.5€= -162.5 €, the –(a+b+c+d) areas of the diagram⁽¹²⁾.

The Net effect can be calculated by the –(c+d) areas of the diagram⁽¹²⁾:

-(c+d)= -{[(Q_S-Q_Sw)x(P_S-P_W)]/2}= -{[(65-40)x2.5]/2}=-(62.5/2)= -31.25 €

Producers gain from the production subsidy and their gains can be calculated by the a+b areas of the diagram⁽¹²⁾: a+b= (a+b+c+d)-(c+d)=162.5-31.25=131.25 €

Subject 4: Several politicians in developed countries are in favor of free trade of goods between countries but strongly against immigration and free exchange of workers among countries. The question is whether one can be in favor of the first and against the second, especially since they are actually against free trade of the production factor of labor.

According to the supporters of the above, immigration is created due to the differences of wages among countries and a certain equalization of wages would eliminate that reason, ignoring actually that a large part of immigration is due to asylum seekers.

Continuing, according to them, free trade of goods between countries can provide the less developed ones with a really large market, the international one, to which they could export the goods at which they have a comparative advantage due to cheap labor, creating the conditions for the price of those goods to rise in a long term base due to the increasing demand for the exporting good. Increased demand for the good leads to an increased demand for labor and consequently, a raise on wages. In that way, free trade would eliminate the abovementioned reason for immigration. Based on that, for example Mundell (1957) sees free trade and immigration as substitutes, arguing that restrictions on free trade create immigration and restrictions of labor factors promotes free trade ⁽¹³⁾.

According to the supporters of the above idea, immigration also reduces the labor endowment of the home country of the immigrants, and consequently the number of consumers. The market of the home country is in other words shrinking. In the same time, immigration increases the host country’s costs for health, security and other public services. Finally, some support that a large amount of foreign workers in a country might create serious unemployment problems to its citizens⁽¹⁴⁾.

However, the above arguments are not generally accepted. Markusen (1983) has proved that free trade and immigration are actually complements in cases where international trade is created for example due to differences in technology, preferences or lack of perfect competition⁽¹⁴⁾. There are also others who argue that immigrants in a free trade environment create a whole new market for trade with goods for which there was no demand before immigration⁽¹⁵⁾. Immigrants also pay taxes in the host country⁽¹⁴⁾.

In conclusion, the idea that a country should promote free international trade and prohibit immigration isn’t always the best solution, since it can be beneficial only under certain circumstances that are not always attainable.

BIBLIOGRAPHY:

⁽¹⁾ THOMPSON, H. (2001) “International Economics: Global Markets and International Competition”. Singapore: World Scientific, p.29,48.

⁽²⁾ KARAGIANNIS, G., KATRANIDIS, S., PALIVOS, T., STOFOROS, C. (2014) International Economics. 2^nd Tutorial Meeting, MBA50: Economics for Managers, Hellenic Open University, 6^th December 2014,p.10.

⁽³⁾ THOMPSON, H. (2001) “International Economics: Global Markets and International Competition”. Singapore: World Scientific,p.29,40-41.

⁽⁴⁾ AGIOMIRGIANAKIS, G.M., VLASSIS, M. (2005) Economics for Managers: Volume 1 International Economic Environment. Patras: Hellenic Open University, p.41.

⁽⁵⁾ KARAGIANNIS, G., KATRANIDIS, S., PALIVOS, T., STOFOROS, C. (2014) International Economics. 2^nd Tutorial Meeting, MBA50: Economics for Managers, Hellenic Open University, 6^th December 2014,p.15.

⁽⁶⁾ KARAGIANNIS, G., KATRANIDIS, S., PALIVOS, T., STOFOROS, C. (2014) International Economics. 2^nd Tutorial Meeting, MBA50: Economics for Managers, Hellenic Open University, 6^th December 2014,p.18-19.

⁽⁷⁾ AGIOMIRGIANAKIS, G.M., VLASSIS, M. (2005) Economics for Managers: Volume 1 International Economic Environment. Patras: Hellenic Open University, p.45.

⁽⁸⁾ THOMPSON, H. (2001) “International Economics: Global Markets and International Competition”. Singapore: World Scientific,p.89-91.

⁽⁹⁾ THOMPSON, H. (2001) “International Economics: Global Markets and International Competition”. Singapore: World Scientific,p.117-8.

⁽¹⁰⁾ THOMPSON, H. (2001) “International Economics: Global Markets and International Competition”. Singapore: World Scientific,p.121-2.

⁽¹¹⁾ KARAGIANNIS, G., KATRANIDIS, S., PALIVOS, T., STOFOROS, C. (2014) International Economics. 2^nd Tutorial Meeting, MBA50: Economics for Managers, Hellenic Open University, 6^th December 2014,p.39.

⁽¹²⁾ SURANOVIC, S.M., (2003) International Trade Theory and Policy. [Online], Chapter 95-1B, Available from: http://internationalecon.com/Trade/Tch95/T95-1B.php[Accessed: 9^th January 2014].

⁽¹³⁾ AGIOMIRGIANAKIS, G.M., VLASSIS, M. (2005) Economics for Managers: Volume 1 International Economic Environment. Patras: Hellenic Open University, p.138-150.

⁽¹⁴⁾ SCHIFF, M., Migration, Investment and Trade: Substitutes or Complements?.[Online] Agent Française de Développement. Availlable from: http://www.afd.fr/webdav/shared/PORTAILS/PUBLICATIONS/EUDN/EUDN2006/Schiff.pdf[Accessed: 14th January 2015].

⁽¹⁵⁾ MARJIT, S., BELADI, H. Complementarily between Trade and Factor Movement: Revisiting Mundell-Markusen Propositions. KeiO Associated Repository of Academic Resources. Available from:

http://koara.lib.keio.ac.jp/xoonips/modules/xoonips/download.php/AA00260492-20020001-0057.pdf?file_id=28397[Accessed: 14th January 2015].