Analysis of Borrower and Lender Households
| ✅ Paper Type: Free Essay | ✅ Subject: Economics |
| ✅ Wordcount: 776 words | ✅ Published: 29 Aug 2017 |
Macro Comp Question 1 August 2015
Suppose there are two types of households in the economy. “Borrower” households borrow funds from “lender” households to purchase housing. Borrower and lender households differ in two ways: first, only borrowers value housing, while both types value non-durable consumption. Second, borrowers discount future utility flows more heavily than lenders: 0 < βB < βL < 1. Both borrowing and lending are subject to constraints.
First, consider the problem of borrowers. Borrowers maximize the expected discounted value of period utility flows with an infinite horizon, where the period utility flow in period t depends on both housing consumption H and non-housing consumption C, as follows:
∞
(1)Max E0 ∑ (βB)t [u(CBt) + w(Ht)]
t=0
where u(C) and w(H) are increasing flow utility functions. Housing depreciates at the rate δ, between 0 and 1. There are no costs of adjustment for housing. Households enter period t with Ht units of housing, and have (1-δ)Ht units of housing available to retain or sell at the end of the period. In period t they choose their housing for next period Ht+1. The house price in period t is Pt, which may be time varying and stochastic. Non-housing consumption is the numeraire, with constant price 1.
In period t, borrowers may borrow Dt+1 ≥ 0 in funds from lender households, at a risk-free interest rate Rt+1, which may be time varying but is known at t. Borrowing is limited to a fraction of the value of next period’s housing stock by the following inequality constraint:
(2)Dt+1≤ θ Pt Ht+1
Borrower households enter period t with a stock of debt RtDt which they must repay to lenders, and receive an endowment of non-durable consumption goods Yt. The household’s period budget constraint is given by
(3) CBt + Pt Ht+1 = Yt + (1 – δ) Pt Ht – RtDt + Dt+1
(a) [5 points]: Identify the minimum set of exogenous and endogenous state variables and the minimum set of control variables, and write down the Bellman Equation for the borrower’s problem. Don’t forget the inequality constraint (2); let μt denote the multiplier on this constraint.
(b) [20 points]: Take first order and envelope conditions, and state the complementary slackness condition. Derive two Euler equations: one involving only μt and values of u'(C) at t and t+1, and the other involving μt, values of u'(C) at t and t+1, and w'(H) at t+1.
Next, consider the problem of lenders. They also maximize expected discounted utility over an infinite horizon, but their period utility does not include housing:
∞
(4)Max E0 ∑ (βL)t u(CLt)
t=0
In period t, lenders may give loans Lt+1 ≥ 0 to borrowers at a risk-free interest rate Rt+1. Lending is limited by the following inequality constraint, where L ≥ 0 is a given parameter:
(5)Lt+1≤ L
Lender households enter period t with a stock of loans RtLt for which they receive payment from borrowers, and receive an endowment of non-durable consumption goods Xt. The lender household’s period budget constraint is given by
(6) CLt = Xt + RtLt – Lt+1
(c) [5 points] Identify the minimum set of exogenous and endogenous state variables and control variables and write down the lender’s Bellman equation. Let λt denote the multiplier on the inequality constraint (5).
(d) [15 points] Take first order and envelope conditions and state the complementary slackness condition. Derive the Euler equation for non-durable consumption.
In equilibrium, housing demand by the borrowers must equal the fixed housing supply H in all periods. Also, supply and demand for loans must equal: Dt+1 = Lt+1 in all periods. In equilibrium, at least one of the inequality constraints (2) and (5) will bind; both may bind.
Important: for the rest of the problem, assume that the utility function for nondurable consumption for both borrowers and lenders is linear: u(C) = C.
(e) [15 points] Below is a picture of the borrower’s demand curve for funds for this model. Using the complementary slackness condition and the Euler Equation for nondurable consumption from part (b), explain the shape of this demand curve and express the maximum interest rate RMax and the maximum quantity of funds DMax in terms of model parameters and the housing price P.
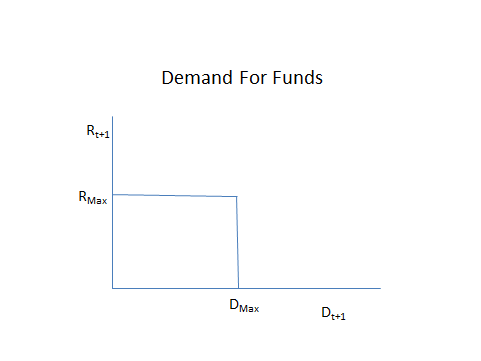
(f) [20 points] Using the complementary slackness condition and the Euler Equation from part (d), draw a picture of the lender’s supply curve of funds, expressing any threshold interest rates or quantity of funds in terms of model parameters.
(g) [20 points] Equilibrium in the market for funds can be expressed graphically by combining the supply and demand curves for funds in a single graph. Prove that for a given θ, the equilibrium interest rate will equal (1/βL) when L is sufficiently large, and (1/βB) when L is sufficiently small. (Draw one graph for a high value of L and another for a low value of L).
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


