Inverse Matrix Condition Number
| ✅ Paper Type: Free Essay | ✅ Subject: Computer Science |
| ✅ Wordcount: 2029 words | ✅ Published: 22 Jun 2018 |
Inverse Matrix and Condition No.
- Saswati Rakshit
Contents (Jump to)
Aim:
Consider 2 random matrices B and C of size 8×8 and write a cpgm / matlab to find A to satisfy the bellow condition:
If A×B = C
Prove A = C×B-1
And repeat the pgm for matrix of size 32×32 and 128×128.
Scope/Application:
In many applications we require inversion of matrix. In Linear Algebra, if A×B=C, and from B and C we can compute A where A=C×B-1.
Stimulus-Response Computations
In this framework, a system is provided with an input, called a stimulus, and the resulting response of the system is measured. Some typical examples of stimuli are visual scenes i.e. if we increase incident light’s intensity then scene’s brightness will increase. The general goal is to find a function that accurately describes the relation between stimulus and response.
Many systems can be modeled as a linear combination of equations, and thus written as a matrix equation:
[Interactions]{response}= {stimuli}
The system response can thus be found using the matrix inverse.
Sometimes in image processing application if we have noisy image matrix and if we know what the noise matrix was added we can find the clear image by multiplying noisy image matrix with inverted noise matrix.
Intro/Basics:
We have considered two 8×8 matrices B and C. We suppose A×B = C. Now by performing matrix multiplication on A and B we get C. Now we have to compute A from B and C.
So A×B = C and we have to proof A = C×B-1.
It is conceptually easy to compute A×B = C and to find A = CB-1 for 2 dimensional matrices. But for large dimensional matrices it is not possible to easily compute because there is some round off errors in A which is the result of B-1 related to B’s condition number. Thecondition numberof a function with respect to an argument measures how much the output value of the function can change for a small change in the input argument.
The condition number of a regular (square) matrix is the product of the norm of the matrix and the norm of its inverse and hence depends on the kind of matrix-norm. Condition number of a square nonsingular (invertible) matrix A is defined by:
cond ( ) = ||
) = || ||·||
||·|| ||
||
where the ||·|| above could be any of the norms defined for matrices. The numerical value of the condition number of an n×n matrix depends on the particular norm used .The norm of a square matrix A is a non-negative real number denoted by ||A||. These matrix norms have the following properties:
1. ||A|| ï€¾ï€ ï€° if A ≠ 0
2. ||ï§A|| ï¼ï§ï¼·ï¼ï¼A|| for any scalar value ï§ï€ ï€
ï€³ï€®ï€ ï¼ï¼A|| ï€«ï€ ï¼ï¼B|| ≤ ï€ ï¼ï¼A|| ï€«ï€ ï¼ï¼B||ï€ ï€
ï€´ï€®ï€ ï¼ï¼AB|| ≤ ï€ ï¼ï¼A||·ï¼ï¼B||ï€ ï€
ï€µï€®ï€ ï¼ï¼Ax|| ≤ ï€ ï¼ï¼A||·ï¼ï¼ ||ï€ ï€ for any vector
||ï€ ï€ for any vector 
The norm of a matrix is a measure of how large its elements are. It is a way of determining the “size” of a matrix that is not necessarily related to how many rows or columns the matrix has. Three commonly used norms are:
1. The 1-norm:
 =
= 
This is the maximum absolute column sum where simply we sum the absolute values down each column and then take the biggest answer.
2. The inifinity-norm:
 =
= 
This is the maximum absolute row sum where simply we sum the absolute values along each row and then take the biggest answer.
3. The Euclidean norm:
 =
= 
This is the square root of the sum of all the squares.
However, regardless of the norm, this condition number is always greater or equal to 1. If it is close to one, the matrix is well conditioned which means its inverse can be computed with good accuracy. If the condition number is large, then the matrix is said to be ill-conditioned. Practically, such a matrix is almost singular (not invertible), and the computation of its inverse or solution of a linear system of equations is prone to large numerical errors. A matrix that is not invertible has the condition number equal to infinity. Mathematically, if the condition number is less than ∞, the matrix is invertible. Numerically, there are roundoff errors which occur. A high condition number means that the matrix is almost non-invertible. The higher the condition number, the greater is the error in the calculation. This condition number helps to estimate how difficult a matrix will be to numerically invert. This condition number has certain properties:
1. For any matrix A, cond (A) ≥ï€ 1
2. For identity matrix, cond (I) = 1
3. For any matrix A and scalar ï§, cond ï§ï€ A) = cond (A)
4. For any diagonal matrix D = Diag(di), cond (D) = (max |di|)/(min|di|)
A matrix A is ill-conditioned if relatively small changes in the input (in the matrix A) can cause large change in the output (the solution of Ax = b), i.e. the solution is not very accurate if input is rounded. Otherwise it is well-conditioned. If a matrix is ill-conditioned, then a small roundoff error can have a drastic effect on the output. However, if the matrix is well-conditioned, then the computerized solution is quite accurate. Thus the accuracy of the solution depends on the conditioning number of the matrix.
Objective:
To know how to determine the matrix inverse in an efficient manner.
If A×B=C and we have to prove A=C×B-1 where A, B and C are n×n matrices (n = 8, 32, 128) and find out the condition number of matrix using norms and finding accuracy.
System flow:
Steps performed:
1. Taking two matrices B and C of order 8×8.
2. Performing Matrix multiplication and result is stored in matrix A (performed using C Code)
3. Now calculate B-1 (performed using C Code)
4. Now again multiplying C and B-1. We get result matrix which is not accurate.
5. We need to calculate norms and condition number of a matrix (B) so we need to find norms of B and B-1.
We can calculate norms in different way. Here we have used most popularly used 3 types of norms to calculate condition number of that matrix (B) which we need to get in inverse form.
The norms are:
- 1-norm
 =
= 
- Infinity-norm
 =
= 
iii) Euclidean norm  =
= 
6. Now we use norms to find condition number of matrix B by using formula
cond (B) = || ||·||
||·|| ||
||
Flow Diagram
















 yes
yes

no

Math
For 2×2 Matrix
First we consider a 2×2 matrix such that
A=  B=
B=
So by multiplying A and B we ge a 2×2 matrix C =
Now We need to prove A=CB-1
So we need to find B-1
B-1 = 0.800 -0.200
-0.600 0.400
So now by doing CxB-1 =  =A (proved)
=A (proved)
Before finding B-1 we can calculate condition number of B for the correctness of above proof,
As we know cond (B) = || ||·||
||·|| ||
||
Condition number using the 1-norm and inifinity-norm:
Formula used
Row Sum taking absolute values
B = 2 13
3 47
Column sum 5 5
(taking absolute values) (max)
Row sum
B-1 = 0.800 -0.200 1.000
-0.600 0.400 1.000
Col Sum 1.4 .6
Applying 1-Norm
 =
= 
= maximum absolute column sum
 = 5,
= 5,  1 = 1.4,
1 = 1.4,
So,
cond1 (B) =  ·
· 1 = 5×1.4= 7
1 = 5×1.4= 7
Applying infinity-norm
 =
= 
= max absolute row sum
 = 7,
= 7,  ∞ = 1
∞ = 1
So,
cond∞ (B) =  ·
· ∞ = 7
∞ = 7
Like this way we have also found condition number using the Euclidean norm which is  =
=  =5.47
=5.47  = 1.095
= 1.095
CondE (B) =  ·
· E = 5.82
E = 5.82
Here cond(B) is low in all cases.so we successfully get A =C.
Because of low condition number of B,the inverse of B is acceptable.
For 8×8 Matrix
A = 1 2 3 4 1 2 2 1
2 3 1 4 3 4 2 1
4 1 3 2 3 3 1 2
2 2 1 4 2 2 2 1
3 2 1 4 3 1 2 1
1 1 2 3 1 2 2 1
1 2 1 2 1 2 1 2
2 2 3 3 2 1 2 2
B= 4 1 3 2 3 3 1 2
2 3 1 4 3 4 2 1
2 2 1 4 2 2 2 1
1 1 2 3 1 2 2 1
2 2 3 3 2 1 2 2
1 2 3 4 1 2 2 1
1 2 1 2 1 2 1 2
3 3 1 3 2 3 1 1
C=A×B=27 30 28 52 27 37 28 20
35 38 42 64 35 46 35 27
42 35 41 59 37 43 31 27
29 29 32 49 28 37 27 22
34 30 35 50 32 39 28 25
22 24 24 41 21 29 22 17
23 25 22 39 22 30 20 15
34 33 30 53 32 40 28 23
B-1= -0.016 -0.429 0.063 0.524 0.063 -0.397 -0.222 0.587
-0.365 0.143 -0.540 0.048 0.460 -0.127 -0.111 0.508
0.095 0.071 -0.381 -0.143 0.119 0.381 -0.167 -0.024
0.270 -0.214 0.921 -0.905 -0.579 0.746 0.278 -0.484
0.206 0.571 0.175 -0.810 0.175 0.159 -0.111 -0.635
0.079 0.143 -0.317 0.381 -0.317 -0.016 0.111 0.063
-0.571 0.071 -0.714 1.857 0.786 -1.286 -0.500 0.643
0.159 -0.214 0.365 -0.238 -0.135 -0.032 0.722 -0.373
A=C×B-1 =0.995 1.983 3.029 3.987 1.029 1.984 2.006 0.979
1.992 2.975 1.035 3.983 3.035 3.980 2.005 0.972
3.989 0.971 3.029 1.984 3.029 2.981 1.006 1.970
1.993 1.980 1.027 3.987 2.027 1.984 2.004 0.977
2.991 1.976 1.027 3.986 3.027 0.983 2.004 0.974
0.996 0.986 2.022 2.990 1.022 1.987 2.004 0.983
0.994 1.986 1.021 1.991 1.021 1.988 1.005 1.982
1.992 1.979 3.028 2.987 2.028 0.983 2.007 1.975
Relative Error for A11=(1-.995)=.005,A12= 0.017 and so on
When we perform C× B-1, we do not get original value of A because of B-1. If B-1 is not accurate we will not get accurate A. To get accuracy of A-1 we need to find condition number of B.
As we know cond (B) = || ||·||
||·|| ||
||
Condition number using the 1-norm and inifinity-norm:
Formula used
Row Sum taking absolute values
B = 4 1 3 2 3 3 1 2 19
2 3 1 4 3 4 2 1 20 (max)
2 2 1 4 2 2 2 1 16
1 1 2 3 1 2 2 1 13
2 2 3 3 2 1 2 2 18
1 2 3 4 1 2 2 1 16
1 2 1 2 1 2 1 2 12
3 3 1 3 2 3 1 1 17
Column sum 16 16 15 25 16 19 13 11
(taking absolute values) (max)
|
-0.016 -0.429 0.063 0.524 0.063 -0.397 -0.222 0.587 -0.365 0.143 -0.540 0.048 0.460 -0.127 -0.111 0.508 0.095 0.071 -0.381 -0.143 0.119 0.381 -0.167 -0.024 0.270 -0.214 0.921 -0.905 -0.579 0.746 0.278 -0.484 0.206 0.571 0.175 -0.810 0.175 0.159 -0.111 -0.635 0.079 0.143 -0.317 0.381 -0.317 -0.016 0.111 0.063 -0.571 0.071 -0.714 1.857 0.786 -1.286 -0.500 0.643 0.159 -0.214 0.365 -0.238 -0.135 -0.032 0.722 -0.373 |
B-1 =
For B-1, Row sum (max) taking absolute values = 6.428 (7th row)
and column sum(max) taking absolute values = 4.906 (4th column)
Applying 1-Norm
 =
= 
= maximum absolute column sum
 = 25,
= 25,  1 = 4.906,
1 = 4.906,
So,
cond1 (B) =  ·
· 1 = 25×4.906 = 122.65
1 = 25×4.906 = 122.65
Applying infinity-norm
 =
= 
= max absolute row sum
 = 20,
= 20,  ∞ = 6.428
∞ = 6.428
So,
cond∞ (B) =  ·
· ∞ = 20×6.428 = 128.56.
∞ = 20×6.428 = 128.56.
Like this way we have also found condition number using the Euclidean norm which is = 17.83.
So here we can say that as the condition number of matrix B is high for all three cases, therefore the inverse of this matrix is showing numerical roundoff errors.
Concept of Relative Error and Condition Number
assume A is nonsingular and Ax = b if we change b to b + ∆b, the new solution is x + ∆x with
A(x + ∆x) = b + ∆b the change in x is ∆x = A-1∆b
‘condition’ of the solution
• the equations are well-conditioned if small ∆b results in small ∆x
• the equations are ill-conditioned if small ∆b can result in large ∆x
[Singular matrix:A square matrix is called singular matrix if it’s determinant is zero.i.e. a singular matrix is not invertible]
Example:
Consider the linear system Ax = b with
So 
 =
=
So here we easily find x=
Now ,we change a small in b.let change in b is ∆b=
So changed value =
=
and solving the system A =
= 
we get  =
= A=
A=
where x= changed to
changed to  =
= due to small change in b.
due to small change in b.
Now to calculate least condition number of the system we need to find Relative Error in the output and relative error in the input.
Here we have
relative error in the input/relative residual.  = 0.01
= 0.01
Relative Error in the output  =1
=1
As we know,
If condition number is closed to 1 then relative error and relative residual will be close.
The condition number is defined by:
Relative error in the output =Condition number × Relative error in the input.
So,condition number= 1/.01=100
A matrix has high condition number is related to the fact that A is close to the singular
matrix B=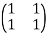
The following result shows that 1/cond(A) indicates how close A is to a singular matrix.Here cond(A) is 100 so, 1/cond(A)=.01 which is close enough.
Description:
The condition number associated with the linear equation Ax=bgives a bound on how inaccurate the solutionxwill be after approximation. This is before the effects of round-off error are taken into account; conditioning is a property of the matrix.
Weshould think of the condition number as being the rate at which the solution,x, will change with respect to a change inb. Thus, if the condition number is large, even a small error inbmay cause a large error inx. On the other hand, if the condition number is small then the error inxwill not be much bigger than the error inb.
The condition number may also be infinite, but this implies that the problem does not possess a unique, well-defined solution for each choice of data — that is, the matrix is not invertible, and no algorithm can be expected to reliably find a solution.
For large dimensional matrix such as for 32×32 and 128×128, the condition number is high and so inverse of that large dimensional matrix will give much error in output.
Codes and Output
Matrix multiplication
int main()
{
int m, n, p, q, c, d, k, sum = 0;
int A[10][10], B[10][10], C[10][10];
printf(“Enter rows and columns of An”);
scanf(“%d%d”, &m, &n);
printf(“Enter the elements of An”);
for (c = 0; c < m; c++)
for (d = 0; d < n; d++)
scanf(“%d”, &A[c][d]);
printf(“Enter rows and columns of Bn”);
scanf(“%d%d”, &p, &q);
printf(“Enter the elements of Bn”);
for (c = 0; c < p; c++)
for (d = 0; d < q; d++)
scanf(“%d”, &B[c][d]);
for (c = 0; c < m; c++) {
for (d = 0; d < q; d++) {
for (k = 0; k < p; k++) {
sum = sum + A[c][k]*B[k][d];
}
C[c][d] = sum;
sum = 0;
}
}
for (c = 0; c < m; c++) {
for (d = 0; d < q; d++)
printf(“%dt”, C[c][d]);
printf(“n”);
}
getch();
}
Matrix inverse
#include
#include
int main()
{
float a[10][10],b[10][10],tem=0,temp=0,temp1=0,temp2=0,temp4=0,temp5=0;
int n=0,m=0,i=0,j=0,p=0,q=0;
printf(“Enter size of 2d array(Square matrix) : “);
scanf(“%d”,&n);
for(i=0;i { for(j=0;j { printf(“Enter element no. %d %d :”,i,j); scanf(“%f”,&a[i][j]); if(i==j) b[i][j]=1; else b[i][j]=0; } } for(i=0;i { temp=a[i][i]; if(temp<0) temp=temp*(-1); p=i; for(j=i+1;j { if(a[j][i]<0) tem=a[j][i]*(-1); else tem=a[j][i]; if(temp<0) temp=temp*(-1); if(tem>temp) { p=j; temp=a[j][i]; } } //row exchange in both the matrix for(j=0;j { temp1=a[i][j]; a[i][j]=a[p][j]; a[p][j]=temp1; temp2=b[i][j]; b[i][j]=b[p][j]; b[p][j]=temp2; } //dividing the row by a[i][i] temp4=a[i][i]; for(j=0;j { a[i][j]=(float)a[i][j]/temp4; b[i][j]=(float)b[i][j]/temp4; } //making other elements 0 in order to make the matrix a[][] an indentity matrix and obtaining a inverse b[][] matrix for(q=0;q { if(q==i) continue; temp5=a[q][i]; for(j=0;j { a[q][j]=a[q][j]-(temp5*a[i][j]); b[q][j]=b[q][j]-(temp5*b[i][j]); } } } printf(“nnn”); printf(“Inverse of the matrix using Guass jordan elimination method:nn”); for(i=0;i { for(j=0;j { printf(“%.3f”,b[i][j]); } printf(“n”); } getch(); } #include #include int main() { int i,j,n,p,x=0,m=0,q,z=0,i1,j1; float Cond_A,poo,a[5][5],b[5],c[5],A[50][50],B[50][50],k[50],l[50]; printf(“n———————————————— n”); printf(“Program to find condition number of a matrix using infinity-norm”); printf(“n———————————————— nn”); printf(“Enter rows and columns of An”); scanf(“%d%d”, &m, &n); printf(“Enter the elements of An”); for (i = 0; i < m; i++) for (j = 0; j < n; j++) scanf(“%f”, &A[i][j]); for(i=0;i { b[x]=0;c[x]=0; for(j=0;j { b[x]=b[x]+A[i][j]; } ++x; } for(i=0;i //FINDING LARGEST { if(b[i]>m) m=b[i]; } printf(“largest row sum is %d”,m); printf(“nnEnter rows and columns of inv[A]n”); scanf(“%d%d”, &p, &q); printf(“Enter the elements of [A]n”); for (i1 = 0; i1 < p; i1++) for (j1 = 0; j1 < q; j1++) scanf(“%f”, &B[i1][j1]); for(i1=0;i1 { k[z]=0;l[z]=0; for(j1=0;j1 { k[z]=k[z]+B[i1][j1]; } ++z; } poo = k[0]; for(i1=1;i1 //FINDING LARGEST { if(k[i1]>poo) poo=k[i1]; } printf(“largest row sum is %f”,poo); Cond_A=m*poo; printf(“nnCondition number of A is %f”,Cond_A); //return 0; getch(); } If we work with a foggy image matrix(C) and we know the fog matrix(B) added to that image and the relation A×B = C exist we will know whether it is possible to get the clear image matrix(A) by doing C×B-1 calculating condition number of matrix B. If the condition number of matrix B is high then it is not possible to get accurate A from C×B-1 as roundoff errors will increase.
Matrix Condition Number

Future works:
References:
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


