Supramolecular Self-assembly of New Dendritic Molecules

1.    Introduction

Liquid crystal(LC) is considered as the midway between an isotropic liquid and a crystalline solid, they possess characteristics of liquid such as high fluidity , inability to support shear and coalescence of droplets, at the same time have the properties of solid crystals for example exhibiting anisotropy in their electrical , optical and magnetic properties.[1] Otto Lehman was the first to suggest the name liquid crystal in 1889 to identify this state.^[2] Other names including mesomorphic state, Para crystal, mesomorphs and ordered fluids were also used in the literature. It is further classified into two categories one is known as thermotropic LC, formed by melting a crystalline solid, and the second one lyotropic LC, which is formed by mixing of solutions, such as aqueous solutions of tobacco mosaic virus (Bawden and Pirie, 1937; Oster, 1950) and certain polymers (Robinson, Ward, and Beevers, 1958).^[3]  Four Liquid crystals (or mesophases): nematic , smectic , cholesteric(chiral) and columnar are commonly observed ,depending on the way molecules arrange themselves and their different range orders. Liquid crystals today are well famous for their use in flat panel displays, their use is not just limited to that but also their potential in photonics, liquid crystals-functionalized polymer fibers, liquid crystals elastomeric actuators, food science and pharmacology.[4]

The concept of self-assembly of supramolecules  is utilized in this project and an effort is made to examine the supramolecular self-assembly of some new dendritic molecules, focusing on the molecular design principles of micellar cubic/non-cubic structures. The different tasks that are carried in this project are; Determination of the self-assembled structures, 2D or 3D formed by the new compounds, using mostly X-ray diffraction, Reconstruction of electron density maps, on the basis of collected diffraction intensities and determined lattice parameters and space group, Construction of molecular models, as well as carrying out molecular dynamic simulations, of phases observed, to establish the validity of the structural models of the phases.

2.    Literature review

2.1.                        Self-assembly of supramolecules

Materials possessing liquid-crystalline nature can self-organize into numerous nanostructured phases: layered, columnar, micellar and bi-continuous cubic arrangements, which are formed typically as a result of segregation of immiscible parts(moities) of molecules.[5] Jean-Marie Lehn invented the term supramolecular chemistry as ‘a science dealing with complex molecules capable of self-organization’.^[6] According to him it is the result of intermolecular forces that hold together two or more chemical species, The forces can be hydrogen bonding and hydrophobic interactions. The supramolecules can be processed through two different routes. One is the host and guest chemistry, host being a bigger molecule binds the guest which is smaller molecule based on the same principle as key and lock. The second one is the self-assembly, the spontaneous and reversible organization of molecular units into ordered structures by non-covalent interactions. The discovery of supramolecular chemistry in the LC has increased its applications since 1989 and a lot of work has been carried out in this field. It provides us with the ability to build liquid crystal molecules that are more dynamic.

2.2.                        Dendrons and Dendrimers

Dendrimers are made up of a branched core which further consist of branched arms, these arms are known as dendrons. Dendrimers can be defined as globular, monodisperse macromolecules in which all bonds emerge radially from a central focal point or core with a regular branching pattern.[7]

Dendrimers and dendrons can be viewed as ideal branched polymers, wherein each monomer repeat unit (mru) introduces a new AB_n bifunctional moiety, where n is the number of branches introduced with each monomer, every branched molecule cannot be termed as dendrimers due to the dendritic state properties.^[8] These properties can include core encapsulation along with low intrinsic viscosity in solution are acquired only when globularity is obtained at a certain size threshold.^[9]

Two different methods have been used for the preparation of dendrimers: one is the divergent approach ^[10], starting of growth at the core which then proceeds radially outward towards the periphery of dendrimer, and the second one is known as convergent approach ^[11], growth starting at the periphery of dendrimer and moving inward.

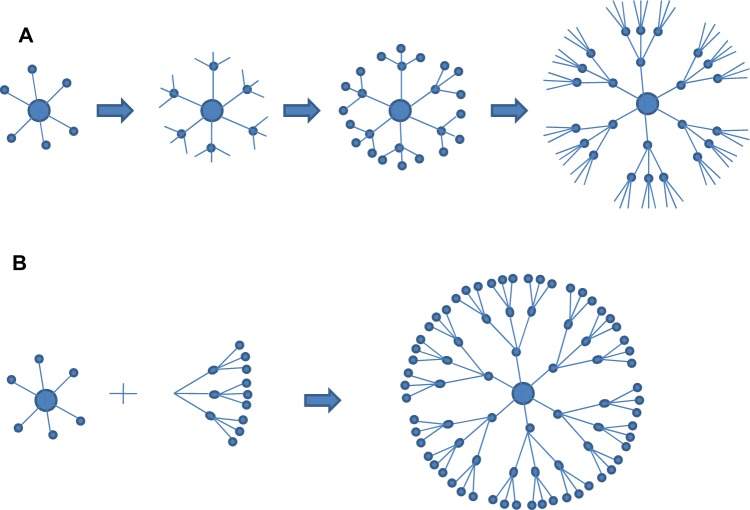
Figure 1. Two methods used for preparation of dendrimers A) divergent approach B) convergent approach.[12]

The self assembly of dendrons and dendrimers can lead to a lot of structures which requires difficult processing conditions therefore an alternative to this is the hyperbranched polymers, which in most of the cases lack the regularity of dendrimers but have the similar properties and are also cheap and easy to process.[13] a comparison of the structures of dendrimers, dendrons, dendronized polymers and hyperbranched polymers are shown in the figure 2.

Figure 2. dendritic polymer structures.[13]

2.3.                        Hexagonal phase formed by dendrons/dendrimers

2.3.1.      Micellar structures

The term ‘micellar’ is used for a self-organized assembly of molecules, which exhibits in the case of cubic phases mostly a spherical shape. Different self-assemblies and conformation that dendritic molecules can arrange themselves in are shown in the Fig.3 below. The different conformations of theses dendron compounds depends on their structure. They will form columnar phase if the dendron is linear taper i.e. cross-sectional area increases linearly with the ‘r’. If the wedge is quadratic then they have the conical shape and will form spheres or micelles, which in turn pack on lattices with 3d long range order giving body-centred cubic(BCC) phase with 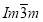symmetry, cubic phase with symmetry and tetragonal phase with P4₂/mnm symmetry (Fig.3b). Thermotropic phases containing small gold nanoparticles(GNP) are also shown in the Fig.3c with a BCC and simple cubic phase. The GNPs when functionalized with a mixture of rod-like nematogens and thioalkyl chains shows three more 3d ordered phases along with the columnar: rhombohedral(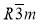), simple hexagonal(p6/mmm) and closed packed face-centered cubic ()(Fig.3d).

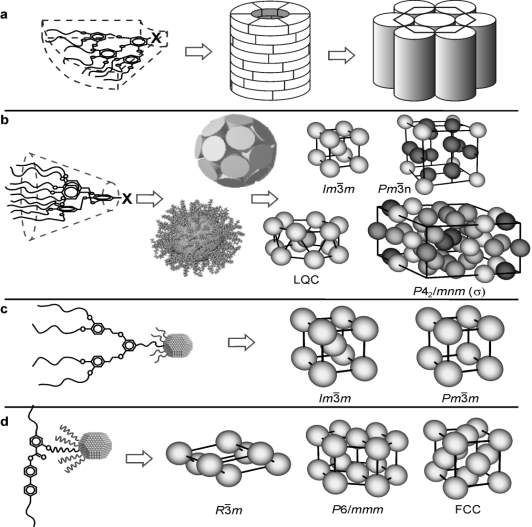
Fig. 3.(a) Self-assembly of dendritic molecules into columnar phase. (b) Self-assembly of conical shape dendrons into micelles which then pack with 3d long-range order giving different periodic structures.^[14] (c) Thermotropic micellar phases based on gold nanoparticles. (d) 3d phases with side-on rod like mesogens attached to gold nanoparticles.

2.3.1.1.  Pm3n cubic phase

The most widely occurring micellar thermotropic phase is the cubic. The structure was determined on the 2nd, 3rd and 4th generation n-dodecyl-terminated benzyl ether dendrons.18 The structure of the cubic phase was first determined on compoundsshown in Fig.5.^[15]The cubic unit cell contains 8 “micelles”, i.e. dendron aggregates, with the mainly aromatic spherical core embedded in a continuum of molten terminal alkyl chains (Fig.4).

Fig. 4. Unit cell of cubic Pm $\bar{3}$

n phase.¹⁸

Fig. 5. Benzylether Percec-type dendrons of generations 1-4, all forming the cubic phase.¹⁴

2.3.1.2.  Micellar body-centered cubic (bcc)

The micellar body-centered cubic (BCC) phase with symmetry is the highest temperature LC phase for all compounds. The unit cell is composed of spherical micelles located at the corners and at the center of the cell (Fig.6).

The graph in the Fig.7 shows the dependency of temperature of alkali metal salts with that of cation diameter ,in this case the salts used were 3,4,5-tris-tetradecyloxybenzoic acid, which shows that BCC phase is always obtained at high temperatures. Wherever the phase is also observed in these salts, it occurs below the temperature range of the BCC.

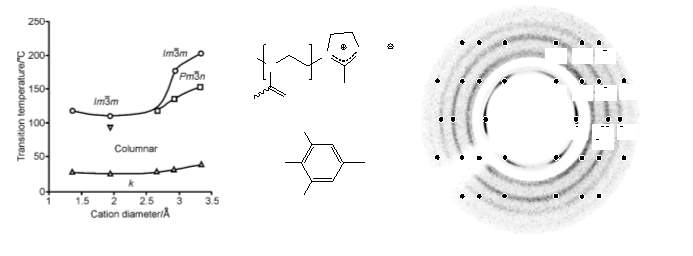Fig. 6. BCC unit cell.

Fig. 7. Left: Transition temperatures of alkali metal salts of 3,4,5-tris-tetradecyloxybenzoic acid  as a function of cation diameter.^[16] Right: X-ray fibre diffraction pattern of the dendronized polyoxazoline.^[17]

The first BCC thermotropic micellar LC phase was determined in a dendronized polyoxazoline , the observed Bragg reflections have their 1/d2 values in the ratio 1:2:3:4:5:6:7 (Fig. 7). Other compounds displaying such are certain non-symmetrical three-arm oligobenzoates, with each arm terminated with three alkoxy tails(Fig. 8).

Fig.8. Non-symmetrical three-arm oligobenzoates compound showing micellar bcc phase.

2.3.1.3.    Micellar tetragonal phase (σ-phase)

The third micellar phase in thermotropic liquid crystals has a large tetragonal unit cell with P4₂/mnm symmetry. The unit cell contains 30 micelles (Fig. 9)^[18]. The micelles have similar size and shape predicted from electron density map. The unit cell contains five different types of micelles crystallographically with different symmetries (Fig. 9). In contrast the eight micelles in the phase are of only two types. The volume of a tetragonal unit cell is 3.6 times that of the cell.

Fig. 9. P4₂/mnm unit cell containing 30 micelles.^[19]

Among all other 3d phases observed in a compound , the P4₂/mnmphase is found at a temperature higher than but lower than BCC phase. The P42/mnm tetragonal phase is amorphous in nature with σ-phase in metal alloys. After the discovery of this phase in LC, it was also found in block copolymers with spherical domains.^[20]

2.3.2.      Liquid Quasicrystals

Crystals are formed as a result of periodic arrangement of atoms but the quasicrystals structure is ordered but not periodic resulting in a pattern that can continuously fill all the available space but lacks in the transitional symmetry.^[21] This structure was first discovered in 1980’s in metal alloys by D.schechtman.^[22] In LC supramolecules this structure was first discovered in 2004, in that structure self-assembly of of a number of dendrons were able to form a micellar phase with no attributable classical space group and with the forbidden 12-fold rotational symmetry.^[23]Some of the taper-shaped dendrons exhibit the dodecagonal phase are shown in Fig. 10^[24].

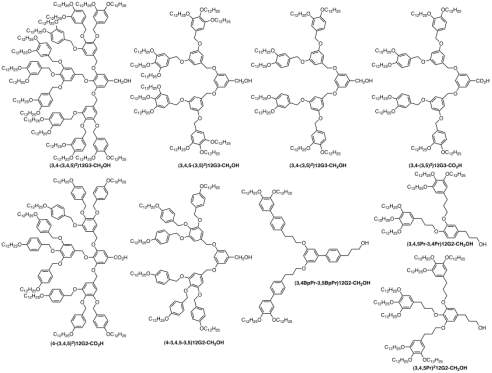
Fig. 10. The dendron compounds found to exhibit the micellar dodecagonal liquid quasicrystal phase. ²³

The term “liquid quasicrystal” (LQC) was named after it was found that the density fluctuation was quasiperiodic. X-ray diffraction on a single domain of the LQC phase clearly showed the 12-fold  symmetry (Fig.11a). The dodecagonal QC consists of layers of thick and light populated planes because they belong to Frank-Kasper. From the Fig. 11b it can be seen that how 2d-dodecagonal symmetry is created just by tilting triangular and square tiles.

Fig. 11.(a) X-ray diffraction of dodecagonal LQC phase. (b) Structure model of the dodecagonal LQC phase. c) Square and triangular tiles, decorated with micelles, of the dodecagonal phase.²²

Quasicrystals provides a complete, isotropic photonic bandgap(PBG) due to which it is considered superior than crystals.^[25] In artificial 2d-QC the PBG has been illustrated with help of  8, 10 and 12 fold rotational symmetries. ^{[26],[27],[28]} It’s applications can be traced in quantum electronic devices, optical computing, distributed feedback mirrors, microwave antennae substrates etc. The possibility of scaling up the characteristic length from  5 nm in the current LQC to that of light wavelength, as has been achieved in block copolymers, raises the prospect of producing self-assembled photonic quasicrystals. It was proposed that the formation of QC are more controlled kinetically than as a result of thermodynamics.^[29]

2.3.3.      Chiral cubic phase

A molecule is chiral if it is not superimposable on its mirror image. Most chiral molecules can be identified by their lack of a plane of symmetry or a center of symmetry. Chiral structures can be formed from double-gyroid structure, which is done eliminating one of its gyroid networks while retaining the other. This structure is consider as an ideal photonic crystal when

on the optical length scale. Chiral micellar cubic and tetragonal P4₂/mnm phases were reported in a number of chiral dendritic compounds , which was confirmed by Circular dichroism CD spectroscopy . The hyperbranched liquid crystalline polymer with chiral terminal ends were reported recentnly, which was prepared by melt-polycondensation of AB2 monomer functionalised with chiral units as shown in the fig. 12[30].

Figure 12. Chiral liquid crystalline components for hyperbranched polymers .

2.4.                        Controlling phase by molecular design

Columnar and cubic phases are mostly formed by dendrons, which then ends up giving most of the thermotropic self-assembled systems. In this section an approach on the basis of quantitative geometrical model is examined, In order to relate the structure of the molecule with the self-assembly they form. Linearly tapered molecules will form columnar phase as they can easily fit into the plane, but if the cross-section of chains are larger it will form conical shape thus ends up in forming spheres. The curves are parabolae in the start with surface of the sphere A(r) = dV/dr ∝ r2 , but after they collide the dv/dr function slowdowns or drops. The  dV/dr decreases to zero once all the space is filled.

Fig. 12. Radial distribution of volume functions dv/dr for different micellar phases.[31]

The dV/dr distribution for BCC differs from those for Cubic and Tetragonal P4₂/mnm in that it has a slightly higher peak and shorter tail. The formation of bcc phase at high temperature is due to change in molecular envelope that is expected from a lateral thermal expansion and longitudinal contraction of alkyl tails. This functions shows that Cubic 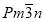and Tetragonal P4₂/mnm are almost find in same system interchangeably, the tetragonal P4₂/mnm usually exist at temperature above 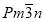and below BCC. The divergence of the wedge-shaped molecule can be approximated in general by using dV/dr = krp. A rough guide to the phase type that such wedge-shaped molecules would form is given as follows. Fig. 12 suggests that,  a higher p favouring the BCC and a lower p favouring the 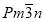phase.

2.4.1.      Synthesis of sodium salts dendrimers

Compounds similar to sodium salts such as tris(alkoxy)benzoate(Fig. 13) will be used in this project for the determination of new dendritic supramolecules assemblies. To show that just by changing the branching or structure the compound can adopt different conformation, Sodium salts 12²18³Na and 18⁵Na , each having one of their three alkoxy chains carrying a further three-way branching point is compared with their counterparts with no branching such as 12³Na and 18³Na . In 18⁵Na all the chains have same length, in 12²18³Na they differ in length considerably.

Fig. 13 sodium salts with different branchings,  123Na and 183Na starts with colh ends at BCC, 122183Na and 185Na  only shows BCC phase.³¹

Results from small angle x-ray diffractions shows that 123Na and 183Na change from Colh-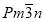-BCC as temperature is increased while the 122183Na and 185Na only show the BCC phase .

Col_h phase for linear wedges are more preferable at low temperature, as in the case of 123Na and 183Na in which the alkyl chains are extended with a few gauche conformers. Increasing the temperature along with the gauche contents makes the chains expands laterally and contracts longitudinally. Thus force the compound to go through columnar-cubic phase transition. Upon further heating the chain ends of cubic 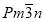phase continues to expand , thus requiring dv/dr function even larger peak and shorter tail, which transforms it into BCC phase .

In case of hyperbranched salts showing only BCC phase is what was predicted from dv/dr analysis. At low temperature the wide aliphatic branches acquires the shape which belongs to the BCC phase. It is believed that this is the only packing pattern that can be adopted by the highly divergent molecules (a dV/dr with a higher peak and a shorter tail).

Experimental section

In this project, a sodium salt FFF-X-22COONa is used. The small angle X-ray scattering experiment was carried out at station I22, diamond light source.  The chemical structure of this salt is shown in fig.14 . some information about its different moieties of FFF-X-22COONa molecule was obtained through Material studio listed in the table below.

Figure 14. the chemical structure of sample FFF-X-22COONa.

Characterization methods:

Experiments were carried out through Small angle X-ray diffraction (SAXD). The wavelength used was 1 Å(0.1nm) (Cu Kα radiations) and the energy used was 12 KeV. SAXD of the powder sample, FFF-X-22 NA Salt, were calculated at different temperature ranges but the sharper peaks appears under 25°C. The process of fitting the diffraction peaks intensities was carried out using Fibrefix and dawndiamond programmes.

A sample C₄₀H₈₂ for calibration was used with known D-spacing(which is the distance from the sample to detector) 52.8 Å is provided for calculation of the radium and parameters of unknown samples. in this experiment the principle of  General Braggs law is used.

                                    Nλ = 2d_hklsinѲ

The dawndiamond software is used to analyse the diffraction pattern of the hyperbranched Na salt(FFF-X-22), which is already calibrated and the q-value(defined as q = 2π / d_hkl ) were estimated from the experimental data using the software. From the q-values the structure or symmetry of the unit cell can be predicted. In order to get clear structure with high intensities q²-values are used. The next step is calculation of miller indices(hkl) which is a tedious job because the q-values alone is not sufficient to give the indices, but with some knowledge of the experimental along with the background and the help of general rules described in the Handbook of liquid crystals, it can be predicted. Once the miller indices is predicted the next step is the finding lattice parameters(a,b) of the unit cell, which is done using the equation.

                                            a = 2π/q_a

                                             b = 2π/q_b

with the help of all these values it can lead us to the calculation of  inter planar spacing (d_hkl). Some typical formulas for different crystal systems are given in the table .

Table . common formulas for d-spacing calculation with parameters (a,b and c) of unit cell. Where α,  β and γ shows the angles between the parameters.[32]

Results and discussions:

SAXD results and phase identification:

The diffraction pattern of FFF-X-22 Na salt was collected at 25°C from SAXD experiments performed at liquid crystals laboratory, Univeristy of sheffield. the results of SAXD pattern of sample are showed below in figure .

Figure 15. Small angle X-ray diffraction results of sample FFF-X-22 Na salt under 25°C.

the plotting curve in the figure shows two-dimensional data of the diffraction after the background is being subtrated from the original results. The figure shows a total of 6 reflection peaks and from the unit cell parameters(, a= 157 Å and b= 108.69 Å ) the sample FFF-X-22 Na salt exhibited a c2mm symmetric rectangular phase.

Figure 16. Diffractogram of FFF-X-22 Na salt, (a) first 5 peaks marked (b) 6^th peak shown .

The figure 2. Shows the diffractogram of SAXD of sample, six Bragg reflections collected by detector is shown in the figure using dawndiamond software. From the iq²-values of each six peaks, there corresponding miller indices(h,k) in 2-d were calculated. There was no specific formula for h,k calculation but through some basic crystallography concepts from literature the values were calculate to be; (11), (20), (02), (22), (31), (13). These values showed c2mm rectangular phase of the unit cell, such indices(hk) fully obeyed the general reflection conditions, h + k = 2n, for the centred plane cell.

Table 1. SAXD data of sample FFF-X-22 Na salt at 25°C.

Reconstruction of density maps of sample and rebuilding three-dimensional structure:

For figuring out the internal structure of the given sample we need to solve a function known as electron density(defined at every point in the unit cell). Those points within the unit cell where this function gives the maximum value is the location of atoms. The structural information is provided by the x-ray diffraction, where the intensity of the scattered rays proportional to the electron density and its transformation to the Fourier is shown through the equation.

$f\left(q\right)=\int \rho \left(x\right)\exp \left(\mathit{irq}\right)\mathit{dr}$

Where $\vec{r}$

vector representing the path difference between parallel waves, $\vec{q}$

vector is defined by $\vec{q}$

=(2π/λ)(k-k₀). Whereas , rq represents the phase deference. The intensity distribution and its relation with the Fourier transform is given by the equation.

                                                                 I(q) = K * |F(q)|*|F^*(q)|

Where F(q) is the fourier transform and F^*(q) is its complex conjugate. To produce correct electron density of the sample phase angles play a key role. For a single unit cell three electron density waves are added and each of them can have different phase angles depending on the conditions of the experiment and data collected. for example, 0 π 0 means first plane has a phase angle 0, the second has 180 and the third one has phase angle 0 again.

Eight possible phase combinations are generated as a result of SAXD pattern only exhibiting three reflection peaks(2ⁿ , n=3 ). For the total 6 Bragg reflections first three were fixed with phase angle and the rest changed accordingly. The eight possible electron density maps(EDM) are shown below.

                      0 0 0                                                     π 0 0                                                    0 π 0

                  0 0 π                                                 π π 0                                                      π 0 π

                                                                                                                                            high

                    0 π π                                                      π π π                                                low

    Figure 17. electron density map of eight possible phase combinations at 25°C. the colour shows difference in densities, in brief words it shows densities from low to high. 0 and π represents the phase angles of planes (hk).   

                                a                                                                                             b 

figure 18. (a) EDM of rectangular columnar phase at 25°C (b)  3-D atomic model for two columns in one unit cell containing 10 molecules  in each disc (c) top-view of rebuild 3-D model( fine optimized and annealed) of Columnar rectangular phase.

The molecular structure of the sample FFF-X-22 Na salt(figure 14.) contains two aromatic rings connected with alkyl chain and with each ring further contains branches of aliphatic chains along with that. The ionic Na forms the core through which it connects with other molecules, corresponds to high densities(purple ) followed by aromatic rings and the least density(yellow and red) is shown by aliphatic branches. From the miller indices and reflections it was confirmed that this sample is going to selfassemble itself into columnar rectangular(Col_r ) c2mm structure,  therefore the most suitable EDM images that contribute to the final structure would be (ππ0) and (πππ) shown in the figure 17. Keeping in view the EDM of the crystal a 3-D atomic model of the crystal unit cell is build with the help of material studio as shown in figure 18. From the volume and parameters of the unit cell it was calculated that each block in the cell will contain 10 molecules which are arranged using the 3-D model. Choosing the more suitable phase combination π π 0, the molecules were equally distributed in each disc to fill out the space. The ionic moieties( CooNa) will accumulate in the centre with each other giving a tightly packed arrangement as shown in the figure 18(b). but that’s not always the case they prefer to arrange themselves more randomly, as being one of the characteristic features of liquid crystals they always keep moving within the crysral.                                                               

Figure 19. 3-D model of fine optimised and annealed crystal structure of FFF-X22-Na salt.

the figure 19. Shows a rough estimation of how these hyperbranched molecules will arrange themselves. As the temperature is increase these molecules may be tilted laterally with expanding branches and occupy all the available space. This image was obtained using material studio inner build function( fine geometric optimization) . 

Non-hyperbranched 12³ Na salt comparison:

non-hyperbranched dendritic polymers  exhibits perfect and ideally branched structures with superior properties but requires harsh processing conditions and are comparatively costly. If we compare the properties of both the hyperbranched and non-hyperbranched polymers they posses same thermal properties(glass transition temperature and degradation) but different solubility, melt viscosity, chemical reactivity, intrinsic viscosity.[33] The differences are due to their dependence on macromolecular architecture. Alkali metal salts that belongs to AB₃ (first generation minidendrons i.e. [(3,4,5)nG1-CO₂M] ) were extensively studied with different lengths of alkali branches and their dependency on the molecular structure to form different LC phases are describes. [(3,4,5)nG1-CO₂M] normally self-assembles into cylinders at low temperatures and spheres at high tempertaures.  One of the simple linear dendritic structure of 12³Na(12 represents the methyl units in alkali group and 3 represents the number of alkyl chains) salt is shown in the figure. Which consist of an aromatic core connected with alkali metal(M=Na) and alkyl chains associated with it.

Figure 20. molecular structure of 12³Na.

The molecular structure of 12³Na as seen from the figure is linear and forms a wedge shape. The different liquid crystal(LC) structures formed by simple linear 12³Na is compared with the more complex structure FFF-x22-Na. while heating the sample 12³Na its corresponding SAXD curves were recorded to analyse their structure. The results indicates that above the crystal melting point it first form columnar hexagonal(c2mm)  phase, then cubic(pm3n) phase and at high temperatures form the BCC(lm3m) phase. All these phases are structurally different if compared with each other.  These transition strongly depends on the alkyl chains length and the temperature, at low temperature and linear lengths it assembles into Col_h but as the temperature is increased, the chains are squeezed along its length and stretched sideways forcing it to  assemble into pm3n cubic phase. As the temperature is further increased the molecules stretches more laterally and contacts longitudinally transforming it into BCC phase. In contrast, the more complicated and wider structure of the hyperbranched Na salt(FFF-X22-Na) in our case contains two aromatic rings with further alkyl branching on each ring self-assemble into columnar rectangular phase at low temperature. This is because the highly divergent molecules are already expanded and contains more molecules(i.e. 20 ) within each unit cell due to which the more preferred LC phase for these molecules are columnar rectangular.

Figure 21. different LC phases that a wedge shaped dendritic structure can form.

[1] Liquid Crystals – an overview | ScienceDirect Topics. (2017). Retrieved July 28, 2019, from Sciencedirect.com website: https://www.sciencedirect.com/topics/agricultural-and-biological-sciences/liquid-crystals

[2] Stephen, M.J. and Straley, J.P. (1974). Physics of liquid crystals. Reviews of Modern Physics, 46(4), pp.617–704.

[3] Ghanem, E., & Al-Hariri, S. (2013). Synthesis and powder X-ray diffraction of new Schiff-base liquid crystal. Liquid Crystals Today, 22(4), 76–81.

[4] Lagerwall, J.P.F. and Scalia, G. (2012). A new era for liquid crystal research: Applications of liquid crystals in soft matter nano-, bio- and microtechnology. Current Applied Physics, [online] 12(6), pp.1387–1412. Available at: https://www.sciencedirect.com/science/article/pii/S1567173912001113 [Accessed 28 Jul. 2019].

[5] Kato, T., Yoshio, M., Ichikawa, T., Soberats, B., Ohno, H. and Funahashi, M. (2017). Transport of ions and electrons in nanostructured liquid crystals. Nature Reviews Materials, 2(4).

[6] Lehn Cryptand Synthesis – an overview | ScienceDirect Topics. (2009). Retrieved from Sciencedirect.com website: https://www.sciencedirect.com/topics/chemistry/lehn-cryptand-synthesis.

[7] Frechet, J.M.J. (2002). Dendrimers and supramolecular chemistry. Proceedings of the National Academy of Sciences, 99(8), pp.4782–4787.

[8] Fréchet, J. M. J., & Tomalia, D. A. (Eds.). (2001). Dendrimers and Other Dendritic Polymers.

[9] Hawker C J, Wooley K L, Fréchet J M J. J Am Chem Soc. 1993;115:4375–4376.

[10] Tomalia, D. A., Baker, H., Dewald, J., Hall, M., Kallos, G., Martin, S., … Smith, P. (1985). A New Class of Polymers: Starburst-Dendritic Macromolecules. Polymer Journal, 17(1), 117–132.

[11] Grayson, S. M., & Fréchet, J. M. (2001). Convergent dendrons and dendrimers: from synthesis to applications. Chemical Reviews, 101(12), 3819–3868.

[12] Khan, R., Ahmad, E., Zaman, M., Qadeer, A., & Rabbani, G. (2014). Nanoparticles in relation to peptide and protein aggregation. International Journal of Nanomedicine, 899.

[13] Marcos, M., Martín-Rapún, R., Omenat, A. and Serrano, J.L. (2007). Highly congested liquid crystal structures: dendrimers, dendrons, dendronized and hyperbranched polymers. Chemical Society Reviews, 36(12), p.1889.

[14] Zeng, X., Ungar, G., Liu, Y., Percec, V., Dulcey, A. E., & Hobbs, J. K. (2004). Supramolecular dendritic liquid quasicrystals. Nature, 428(6979), 157–160.

[15] Balagurusamy, V. S. K., Ungar, G., Percec, V., Johansson, G. (1997) Rational design of the first spherical supramolecular dendrimers self-organized in a novel thermotropic cubic liquid-crystalline phase and the determination of their shape by X-ray analysis. J. Am. Chem. Soc., 119 (7), 1539-1555.

[16] Percec, V., Holerca, M. N., Uchida, S., Cho, W.-D., Ungar, G., Lee, Y., Yeardley, D. J. P. (2002) Exploring and expanding the three-dimensional structural diversity of supramolecular dendrimers with the aid of libraries of alkali metals of their AB3 minidendritic carboxylates. Chem. Eur. J., 8 (5), 1106-1117.

[17] Yeardley, D. J. P., Ungar, G., Percec, V., Holerca, N. M., Johansson, G. (2000) Spherical supramolecular minidendrimers self-organized in an “Inverse Micellar”-like thermotropic body-centered cubic liquid crystalline phase. J. Am. Chem. Soc., 122 (8), 1684-1689.

[18] Gray, G. W. and Winsor, P. A. (eds) (1974) Liquid crystals and plastic crystals, Ellis Horwood, Chichester.

[19] Ungar, G., & Zeng, X. (2005). Frank–Kasper, quasicrystalline and related phases in liquid crystals. Soft Matter, 1(2), 95.

[20] Impéror-Clerc, M. (2005) Thermotropic cubic mesophases. Curr. Opin. Colloid Interface Sci., 9 (6), 370-376.

[21] Steurer, W. (2004). Twenty years of structure research on quasicrystals. Part I. Pentagonal, octagonal, decagonal and dodecagonal quasicrystals. Zeitschrift Für Kristallographie – Crystalline Materials, 219(7).

[22] Shechtman, D., Blech, I., Gratias, D., Cahn, J. W. (1984) Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett., 53 (20), 1951-1953.

[23] Zeng, X. B., Ungar, G., Liu, Y. S., Percec, V., Dulcey, A. E., Hobbs, J. K. (2004) Supramolecular dendritic liquid quasicrystals. Nature, 428, 157-160.

[24] Ungar, G., Percec, V., Zeng, X., Leowanawat, P. (2011) Liquid quasicrystals. Isr. J. Chem., 51 (11-12), 1206-1215.

[25] Chan, Y. S., Chan, C. T., Liu, Z. Y. (1998) Photonic band gaps in two dimensional photonic quasicrystals. Phys. Rev. Lett., 80 (5), 956-959.

[26] Jin, C., Cheng, B., Man, B., Li, Z., Zhang, D., Ban, S., Sun, B. (1999) Band gap and wave guiding effect in a quasiperiodic photonic crystal. Appl. Phy. Lett., 75 (13), 1848-1850.

[27] Zoorob, M. E., Charlton, M. D. B., Parker, G. J., Baumberg, J. J., Netti, M. C. (2000) Complete photonic bandgaps in 12-fold symmetric quasicrystals. Nature, 404, 740-743.

[28] Bayindir, M., Cubukcu, E., Bulu, I., Ozbay, E. (2001) Photonic band gaps and localization in two-dimensional metallic quasicrystals. Europhys. Lett., 56 (1), 41-46.

[29] Xiao, C. H., Fujita, N., Miyasaka, K., Sakamoto, Y., Terasaki, O. (2012) Dodecagonal tiling in mesoporous silica. Nature, 487, 349-353.

[30] Bauer, S., Ringsdorf, H. and Fischer, H. (1993). Highly Branched Liquid Crystalline Polymers with Chiral Terminal Groups. Angewandte Chemie International Edition in English, 32(11), pp.1589–1592.

[31] Yao, X., Cseh, L., Zeng, X., Xue, M., Liu, Y., & Ungar, G. (2017). Body-centred cubic packing of spheres – the ultimate thermotropic assembly mode for highly divergent dendrons. Nanoscale Horizons, 2(1), 43–49.

[32] Hunter, S. M. (2012). A structural and reactivity study of lithium molybdenum nitride  – Enlighten: Theses. Gla.Ac.Uk. https://doi.org/http://theses.gla.ac.uk/93/1/2008Hunter1MSc.pdf

[33] Hawker, C. J., & Fréchet, J. M. J. (1996). Comparison of Linear, Hyperbranched, and Dendritic Macromolecules. Step-Growth Polymers for High-Performance Materials, 132–144. https://doi.org/10.1021/bk-1996-0624.ch007.