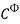Removal of TBP From Aqueous Phase

ABSTRACT

PUREX process involves the use of 30% TBP in Dodecane to extract the fissile materials. However, due to mutual solubility some amount of TBP gets transferred into the aqueous phase. This transferred TBP leads to many environmental problems. Removal of this TBP from aqueous phase is of prime concern which can be done by contacting it with an organic diluent. UNIFAC and Uniquac methods have been used to describe Liquid Liquid equilibrium (LLE) in TBP-Diluent-HNO3 system. Uniquac and UNIFAC Group interaction parameters have been founded to fit the experimental data. Various metal nitrates are also present in the organic phase. These metal nitrates affect the solubility of TBP in aqueous phase. Metal nitrates like Sodium and Calcium nitrate have also been incorporated in model to find out interaction parameters in the presence of metal nitrates like Sodium and Calcium. The obtained parameters will be useful in predicting LLE for the above system and will aid in safe disposal of nuclear waste.

INTRODUCTION

Reprocessing of the used nuclear fuel has always been carried out to reduce the volume of high level radioactive waste and also for their safe disposal. The plutonium uranium extraction (PUREX) process is widely used for reprocessing. This process uses 30% Tri-n-butyl phosphate (TBP) in an inert paraffinic diluent for the separation of uranium and plutonium from the aqueous phase containing nitric acid. Mutual solubility of aqueous and the organic phase leads to the transfer of certain finite amount of TBP in aqueous phase. This transferred TBP decomposes very slowly in the presence of water and nitric acid by hydrolysis to lower organo-phosphate acids at normal operating temperatures leading to many environmental problems. Removal of such dissolved TBP is of direct interest in reprocessing processes as this would enable manifold evaporation of aqueous stream without harming the environment. Various metal elements are also present in the highly radioactive liquid waste solution in nitrate form. The salting out of TBP takes place in the presence of these inorganic nitrates in the aqueous phase. Studies in the presence of various metal nitrates will aid in efficient removal of TBP from aqueous phase.

In order to predict the extent to which TBP could be removed from aqueous phase, a model must be developed to predict the phase behaviour. Such models can be used for designing remediation projects. Estimation of activity coefficients of the mixtures is important for predicting the phase behaviour In order to predict the extent of mass transfer, chemical compositions of the two-phase system at equilibrium needs be predicted first.

Investigators have used various models to predict the LLE. Cheng et al. have calculated the thermodynamic equilibrium constant for the system HNO₃-TBP-n-C₇H₁₆.The activity coefficient of nitric acid was calculated using Pitzer’s equation and those of the components in organic phase was derived from experimental data. Ding et al. have calculated the activity coefficient for 20 binary and 7 ternary systems composed of nC₆H₁₄, nC₇H₁₆, nC₈H₁₈, C₆H₆, cy-C₆H₆, CCl₄, CHCl₃, (C₄H₉)₃PO₄ and UO₂(NO₃)₂.2((C₄H₉)₃PO₄) using head-space gas chromatography. The results are compared with Scatchard-Hilderbald, NRTL and UNIQUAC models. Li et al. has calculated the Vapor-Liquid and Vapor-Liquid-Liquid equilibria of 19 tributyl phosphate systems. Aqueous phase activity coefficients are calculated using Pitzer’s equation. UNIFAC method is used for correlating and predicting the data in organic phase. All the above authors have done work on the systems in the absence of metal nitrates. Interaction parameters for systems in the presence of metal nitrates have not been reported yet.

The objective of the present work to find the UNIFAC and Uniquac group interaction parameters regressed for the experimental data for three systems. These systems comprise of TBP-diluent-HNO₃, TBP-diluent-HNO₃-NaNO₃, TBP-diluent-HNO₃-Ca(NO₃)₂. These parameters will aid in predicting the equilibrium and calculating the number of stages for designing the equipment to remove dissolved TBP.

LIQUID LIQUID EXTRACTION EQUILIBRIA

The organic phase consists of (1) diluent (NPH), (2) TBP, (3) TBP.HNO₃

The dissolution of TBP in NPH and HNO₃ can be represented by eq 1and eq 2.

xTBP_org (TBP)_{x org}(1)

TBP_org + H⁺_aq + NO^3-_aq HNO₃.TBP_org (2)

where the subscripts aq and org denote the species in the aqueous and organic phase.

The thermodynamic equilibrium constant for reaction (2) can be calculated as

a _{HNO3.TBP(org)} a ₃ (3)

K ==

a _H+(aq) a _NO3-(aq) a _TBP(org)a²_±HNO3 a ₂

x₃ γ₃

K = (4)

m_±² γ_±² x₂ γ₂

where a is the thermodynamic activity, x is the mole fraction of the component in the organic phase and γ is the corresponding activity coefficient. m± is the mean molality concentration of electrolyte in the aqueous phase and γ_± is the mean ionic activity coefficient of corresponding electrolytes. Similar procedure as described by Chen et al has been used to predict the LLE with one extraction reaction.

Mean ionic activity coefficient of electrolytes

Pitzer equation is used to calculate the mean ionic coefficient of HNO₃ in all the cases and of Ca(NO₃)₂, NaNO₃ in the presence of metal nitrates.

lnγ_± = – A_Ф+ m (5)

where b=1.2, α=2, A_ɸ = 0.391. I is the ionic strength of solution. The Pitzer parameters for HNO₃, NaNO₃ and Ca(NO₃)₂ are listed in Table 1.

Activity Coefficients of components in organic phase can be estimated using UNIFAC and Uniquac equation.

UNIFAC EQUATION

In a multi-component mixture, the UNIFAC equation for the activity coefficient of component i is given by Equation 3.1.

ln γ_i = ln γ_i^C +ln γ_i^R (6)

The combinatorial part of the UNIFAC model considers the shape and the size of the molecules in the mixture.

ln γ_i^C = 1 – Ji + ln Ji – 5qi( ln (ɸ_i /Θ_i )+ 1 – (ɸ_i /Θ_i ) ) (7)

where, Ji = ( ɸ_i /xi)

The molecule volume fraction ɸ_i , and the molecule surface area fraction Θ_i , are given by

respectively,

ɸ_{i =} xi*r_i/∑_j x_j*r_j and Θ_{i =} xi*q_i/∑_j x_j*q_j (8)

In Equations (3.3), relative molecular volume rs, and relative molecule surface area q, are given by

ri = ∑_k ν_k⁽ⁱ⁾_* R_k and qi = ∑_k ν_k⁽ⁱ⁾_* Q_k (9)

The quantity v_k is the number of subgroups of type k in a molecule of species i. ri is the relative molecular volume and qi is the relative molecular surface area. Group parameters R_k and Q_k are reported by Fredenslund et al.

The residual part of the activity coefficient is given by Equation 10.

ln γ_i^R = ∑_k ν_k^{(i )}[ ln Г_k – ln Г_k⁽ⁱ⁾ ] (10)

where,

k denotes each group in the mixture

ν_k^{(i )} is the number of groups of type k in molecule i

Г_k is the group residual activity coefficient

Г_k⁽ⁱ⁾ is the residual activity coefficient of group k in a reference solution containing only molecules of type i.

The group residual activity coefficient is found by Equation 11.

ln Г_k = Q_k [ 1- ln(∑_m Θ_m ψ_mk) – ∑_m (Θ_m ψ_km /∑_n Θ_n ψ_nm ) ] (11)

where,

Q_k is a group surface area parameter

Θ_m is the area fraction of group m

ψ_mn is the group energy of interaction parameter

ψ_mn = exp(-a_mn + b_mn/T) (12)

Where,

a_mn and b_mn is the group-interaction parameter.

T is the temperature

Group assignment as proposed by Chen et al. has been followed. C₇H₁₆, TBP and TBP.HNO₃ has been broken down into groups CH₃, CH₂, (CH₂O)₃PO, HNO₃.(CH₂O)₃PO. Group volume and surface parameters for above groups have been reported by Cheng et al.

The UNIQUAC model thus consists of two terms: a combinatorial or entropic term, a residual or enthalpic term.

The combinatorial and the residual terms are identical to the terms used in the traditional UNIQUAC equation. The combinatorial, entropic term is

ln γ_i^C = ln(ɸ_i/x_i) +1 – (ɸ_i/x_i) – (z/2)*q_i [ ln(ɸ_i/Θ_i) + 1- (ɸ_i/Θ_i) ] (13) z = 10 is the co-ordination number. xi is the mole fraction, ɸ_i is the volume fraction, Θ_i and is the surface area fraction of component i.

ɸ_{i =} xi*r_i/∑_j x_j*r_j and Θ_{i =} xi*q_i/∑_j x_j*q_j (14)

ri and qi are volume and surface area parameters for component i. The residual, enthalpic term is

ln γ_i^R = q_i [ 1 – ln( ∑_k Θ_kψ_ki) – ∑_k Θ_kψ_ik/(∑_l Θ_lψ_lk) (15)

The parameter ψki is given by

ψ_ki = exp(-u_ki-u_ii/T) (16)

u_ki and u_ii are interaction energy parameters.

Uniquac r and q parameters for C₇H₁₆, TBP and TBP.HNO₃ have been reported by Li et al.

RESULTS AND DISCUSSION

EQUILIBRIUM PREDICTION.

The following equations can be used to predict equilibrium

x₁ + x₂ + x₃ = 1 (17)

x₂⁰ = (x₂ + x₃)/( x₁ + x₂ + x₃) (18)

x₃ γ₃

K = (19)

m_±² γ_±² x₂ γ₂

γ₂ and γ₃ values have been calculated using UNIFAC and Uniquac equation. Knowing equilibrium constant K, m_± calculated mole fractions can be found out., The group interaction parameters are regressed by Least Square Technique to minimize the error between experimental and calculated mole fraction values. The obtained regressed group interaction values in the absence of metal nitrates, in the presence of NaNO₃ and Ca(NO₃)₂ using Uniquac and UNIFAC have been listed in Table. The standard absolute deviation of components in the organic phase is listed in table. The experimental and calculated values of mole fractions have been reported graphically in fig

CONCLUSION

The experimental mole fraction data were correlated using UNIFAC and Uniquac model. The Uniquac and UNIFAC group interaction parameters are capable of predicting mole fraction for TBP-Diluent-HNO₃ in the absence and presence of metal nitrates. Thus these can be effectively used to predict the equilibrium for the removal of dissolved TBP in Nuclear engineering. UNIFAC gives a better prediction as compared to Uniquac in all the cases

LIST OF TABLES

1. Pitzer parameters for calculation of mean ionic activity coefficient
2. Uniquac Group interaction parameters in the absence of metal nitrates
3. Unifac Group interaction parameters in the absence of metal nitrates
4. Uniquac Group interaction parameters in the presence of Sodium metal nitrate
5. Unifac Group interaction parameters in the presence of sodium nitrate
6. Uniquac Group interaction parameters in the presence of calcium metal nitrate
7. Unifac Group interaction parameters in the presence of calcium nitrate
8. Standard absolute deviations between predicted and experimental mole fraction of extracted complexes

Table 1. Pitzer parameters for calculation of mean ionic activity coefficient

Table 2. Uniquac Group interaction parameters in the absence of metal nitrates

Table 3. Unifac Group interaction parameters in the absence of metal nitrates

Table 4. Uniquac Group interaction parameters in the presence of Sodium metal nitrate

Table 5. Unifac Group interaction parameters in the presence of sodium nitrate

Table 6. Uniquac Group interaction parameters in the presence of Calcium metal nitrate

Table 7. Unifac Group interaction parameters in the presence of calcium nitrate

Table 8. Standard absolute deviations between predicted and experimental mole fraction of extracted complexes.