Lewis Acid and Base Lab Report

Introduction

A majority of chemical reactions involve electrons interacting between compounds. It is important to picture these interactions through molecular orbital (MO) theory, where for Lewis acids and bases the movement of electrons between HOMOs (Highest occupied molecular orbital) and LUMOs (Lowest unoccupied molecular orbital). In the real world, some examples of acid and base reactions are baking soda applications for cooking and acid indigestion[1], and kitchen cleaning supplies. The energy gap between HOMOs and LUMOs is often low, allowing the movement of electrons from HOMO to LUMO to proceed with ease.

Borane (BH₃), as a Lewis acid does not satisfy the octet rule and has electron deficiency. It also shows an odd case of existing in equilibrium with B₂H₆, a Lewis acid-base adduct between two boranes.Borohydride (BH₄^–) can act as a Bronsted-Lowry base (proton acceptor) with acids (proton donor). However, unlike borohydride, BH₃ and B₂H₆ is a Lewis acid (electron pair donor) and it donates electron lone pairs to empty orbitals of bases (electron pair acceptors).

IR spectroscopy is a powerful tool used to identify bond stretches for analytes. It also has practical uses for isotope labeling experiments. Several factors relating to equations 1-5 are taken into account for IR stretching. These equations are further explained and applied in the results and discussion section of the paper.One aspect of IR stretching relates to Hooke’s law, where it explains the force for the stretch directly proportional to amount of stretch[2]. Since the amount of stretch depends on the mass of atom which decides the bending and stretching of bond, Hooke’s law (1) is applied to measure potential energy E.

Figure 1 mechanistically shows how BH₄^– reacts with ^tBuNH₃Cl to form H₃B-NH₂^tBu. BH₄^– acts as a Bronsted Lowry base, where the hydrogen atom accepts a proton to form hydrogen gas.

E(x) = $\frac{1}{2}k{x}^2$

(k = force constant) (1)

$E_n\left(n+\frac{1}{2}\right)\mathit{hv}=\left(n+\frac{1}{2}\right)\mathit{hv}=\left(n+\frac{1}{2}\right)h\left(\frac{1}{2\pi }\right)\sqrt{\frac{k}{u}}=\left(n+\frac{1}{2}\right)\mathit{hw}$

  (2)

(n = 0,1,2,….)

ω = vibrational frequency ( $\sqrt{\frac{k}{\mathrm{\mu }}})$

 (3)

$\mathrm{\mu }$

(reduced mass) = $\frac{m_A*m_B}{m_A+m_B}$

 (4)

$\frac{v\left(\mathit{BD}\right)}{v\left(\mathit{BH}\right)}=\sqrt{\frac{u\left(\mathit{BH}\right)}{u\left(\mathit{BD}\right)}}$

 (5)

Figure 1) Mechanism of reaction of BH₄^– and ^tBuNH₃Cl

Experimental

All chemicals and instruments were provided from the IU chemistry department and chemicals were used without any further purification. Spectrum 100 FT-IR spectrometer from Perkin Elmer was used for IR spectroscopy. Spartan 16 was used for computational analysis.

Synthesis of the Lewis Acid-Base Adduct

Tert-butyl ammonium chloride (1.304 g, 0.012 mol) was added to THF (15 mL) were stirred at room temperature. Powdered NaBH₄ (0.200 g, 0.0053 mol) was added during mixing, where gas evolution (H₂) was observed. While mixing, Additional THF (10 mL) was added to the mixture and was stirred for an additional 1.5 hours and filtered with suction filtration for removal of insoluble materials. 5 drops of the solution were added to a salt plate (KBr) for IR spectroscopy. IR (KBr, cm^-1): 2656, 2554, 2452, 1837, 1552, 1349, 1227, 1065, 460. The melting point of Duetero was 53.2-102 $℃$

and Melting point of Proteo was 82-96 $℃$

for the product. For isotope labeling analysis, NaBD₄ (0.210 g, 0.0056 mol) was added in place of Na BH₄ and followed identical procedures, where gas evolution (DH) was also observed.

Result and discussion

Table 1) Energy level calculations HOMO and LUMO of BH₃, BF₃, ^tBuNH₂, and N(CH₃)₃ Data were analyzed based on the Spartan calculations.

Borane (BH₃) and boron triflouride (BF₃) were defined as Lewis acids considering their ability to accept electrons. Both BH₃ and BF₃ have vacant electron sites, and they accept electrons from the HOMO of Lewis bases to fill their empty pi orbitals. On the contrary, ^tBuNH₂ and N(CH₃)₃ were identified as Lewis bases due to their rich electron environments.

The LUMO energy of BH₃ (-1.8 eV) was lower than BF₃ (1.0 eV). Because BF₃ is stronger acid than BH₃. Fluorine is more electronegative than hydrogen, causing inductive effects on boron, and the electron density of boron is lower in boron trifluoride compared to borane. Thus, the energy of BH₃ is shown to be lower than BF₃, and BF₃ is considered to have greater acidity. The boron atom of BF₃ is a better electron acceptor than for BH₃[3].

The HOMO energy of ^tBuNH₂ (-6.2 eV) was lower than that of N(CH₃)₃ (-5.6 eV). This difference in energy is explained by the lone pair of N(CH₃)₃ concentrated on nitrogen atom, while for ^tBuNH₂, the electron density is distributed to the C-H bonds. Thus, N(CH₃)₃ has higher HOMO energies and its ability to donate electrons is greater.

^tBuNH₂, N(CH₃)₃ are Lewis bases with high HOMO energies, and donate electrons to borane and boron trifluoride to fill vacant electron sites. Lewis acids tend to accept electrons from Lewis bases to fill out empty sites of electrons and stabilizes the HOMO. LUMO has empty electron sites, so lower energy LUMOs indicate that Lewis acids are electrophilic, while higher energies of HOMOs indicate a compound being a Lewis base due to their active donation of electrons to the LUMO. Regarding this theory, bond interaction between the HOMO of ^tBuNH₂ and the LUMO of BH₃ is shown in Figure 2 in the form of an MO diagram.

Figure 2) ^tBuNH₂ and BH₃ MO diagram

Figure 3) Spartan IR spectrum (BH₄^–): B-H stretch frequency 2187cm^-1 (Highest Intensity)

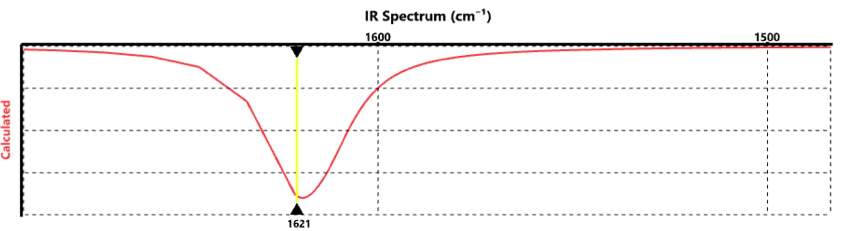
Figure 4) Spartan IR spectrum (BD₄^–): B-D Stretch Frequency: 1621 cm^-1 (Highest Intensity)

Figure 5) Spartan IR spectrum (D₃B-NH₂(^tBu)): B-D Stretch Peak: 1794 cm^-1 (Highest Intensity)

Figure 6) Spartan IR spectrum (H₃B-NH₂(^tBu)): B-H Stretch Frequency: 2424 cm^-1 (Highest Intensity)

Computational isotopic labeling experiments were conducted and analyzed using Spartan IR calculations. For BD₄^–, and BH₄^–, the highest peak for the B-D stretch was 1621 cm^-1 and for the B-H stretch was 2187 cm^-1. Similar differences are shown for D₃B-NH₂(^tBu) and H₃B-NH₂(^tBu) as well. IR stretches for B-N around 1100 cm^-1 to 800 cm^-1 are observed for H₃B-NH₂(^tBu) and D₃B-NH₂(^tBu) as well. The difference between B-H and B-D peaks are explained using equations (4) and (5). Equation (4) shows the reduced mass calculation for boron and hydrogen. Equation (5) is used to compare when a particular peak of the IR spectrum arises predominantly from band stretching of B-H and B-D. Peaks corresponding to B-H and B-D showed different IR stretches and agreed with calculated estimations. Sample calculations of equations (4) and (5) are shown below.

  $\mathrm{\mu }=\frac{m_B*m_H}{m_B+m_H}=\frac{(10.81)(1.01)}{\left(10.81\right)+(1.01)}=0.92$

   (6)

  $\frac{v\left(\mathit{BD}\right)}{v\left(\mathit{BH}\right)}=\sqrt{\frac{u\left(\mathit{BH}\right)}{u\left(\mathit{BD}\right)}}=\sqrt{\frac{0.92}{1.74}}=0.727$

 (7)

  $\frac{v\left(\mathit{BD}\right)}{v\left(\mathit{BH}\right)}=\frac{B–\mathit{D\; stretch}}{B–\mathit{H\; stretch }}=\frac{1621{\mathit{cm}}^{–1}}{2187{\mathit{cm}}^{–1}}=0.741$

 (8)

Figure 6) IR spectrum of reactant B-H peak  

Figure 7) IR spectrum of reactant B-D peak

Figure 8) IR spectrum of ^tBuNH₂-BH₃ peak

Figure 9) IR spectrum of ^tBuNH₂-BD₃ peak

Table 2) Bond stretch wavenumber values

The ratio from the actual B-H stretch (2359 cm^-1) to experimental B-H stretch (2410 cm^-1) was 0.98, which was reasonable considering actual to experimental ratio values under 1.7 to be acceptable. The ratio of the actual B-D peak (1634 cm^-1) to the experimental B-D peak (1644 cm^-1) was also reasonable at 0.99. These ratio values indicate reliable experiment results, while minor shifts of IR peaks have been observed due to hydrated samples.

The shift in wavenumbers correlate to changes in molecular interactions. Stronger bonds and lighter molecules will absorb at higher frequencies, while heavier molecules absorb at lower frequencies[4]. Thus, B-H bonds will absorb at higher frequencies and B-D bonds absorb at lower frequencies. Equation (5) shows how differences in mass cause these shifts and allows successful estimations of how much the ratio is.

Comparing the data with groups’ NaBD₄ IR spectrum data, it was found that the other group’s B-D peaks were sharper and had minimal to no THF and water peaks shown in the IR spectrum. The cause of such error was created due to excessive hydration of THF on the KBr plate. To effectively filter impurities, excessive time lengths of suction filtration were performed in addition to use of excessive amounts of THF. A large region around 3440 cm^-1 corresponding to THF was observed along with huge water peaks inevitably due to wet KBr as observed in the blank sample.

Table 3) $v$

Ratios for B-D to B-H stretches (Calculations follow equation (8))

Ratios for the IR stretches obtained experimentally agree with the theoretical values. However, differences in ratios for the obtained experimental data were due to impurities and unreacted reagents. More sophisticated separation methods such as column chromatography need to be employed to successfully purify samples. These calculations also assume ideal gas phase reactions and fails to account for interactions with the solvent. 

Table 4) Melting point of D₃B-NH₂^tBu

The melting point was not accurate enough due to impurity and fast evaporation. The range between the initial and final temperature was significantly large, indicating impure samples. However, the range falls within the actual melting point of the product.

Conclusion

 A series of experiments have been performed to understand reactions of Lewis acid and base by relating to the HOMOs and LUMOs of certain chemicals. By reacting a Lewis acid and base through chemical synthesis and analyzing the reaction by means of IR spectroscopy and computational studies, an understanding of electron exchange between chemicals is solidified. IR and computational data support proof of how Lewis acids such as BH₃ tend to accept electrons and bases like ^tBuNH₂ may act as electron donors.

References

• Calbreath, D. Lewis acids and bases. cK12. https://www.ck12.org/chemistry/lewis-acids-and bases/rwa/Watch-It-Fizz/
• Nave, R. Elastic potential Energy. HyperPhysics http://hyperphysics.phastr.gsu.edu/hbase/pespr.html
• Andy, S. Principles of General Chemistry: Lewis Acids and Bases; Creative commons: California, 2012.
• Ryu, R. S. Noda I. Jung, Y. M. Positional Fluctuation of IR Absorption Peaks: Frequency Shift of a Single Band or Relative Intensity Changes of Overlapped Bands. American Laboratory. 2011 https://www.americanlaboratory.com/913-Technical-Articles/1244-Positional-Fluctuation-of-IR-Absorption-Peaks-Frequency-Shift-of-a-Single-Band-or-Relative-Intensity-Changes-of-Overlapped-Bands/

[1] Calbreath, D. Lewis acids and bases. cK12

[2] Nave, R. Elastic potential Energy. HyperPhysics

http://hyperphysics.phastr.gsu.edu/hbase/pespr.html

[3] Andy, S. Principles of General Chemistry. 2012

[4] Ryu, R. S. Noda I. Jung, Y. M. American Laboratory. 2011