Computational Study of Carbon Nanotube (CNT)

The C, Si, Ge Doped (6,3) Chiral BNNTs: A Computational Study

Abstract: Electronic structure properties including bond lengths, bond angles, dipole moments (µ), energies, band gaps, NMR parameters of the isotropic and anisotropic chemical shielding parameters for the sites of various atoms were calculated using density functional theory for C , Si , Ge doped (6,3) Chiral BNNTs. The calculations indicated that average bond lengths were as: Ge-N > Si-N > C-N and Ge-B > Si-B > C-B. The dipole moments for C, Si, and Ge doped (6, 3) Chiral BNNTs structures show fairly large changes with respect to the pristine model.

Keywords: NMR, Nanotube, DFT, Dipole moment

1. Introduction

Since the early times that carbon nanotube (CNT) was discovered by Iijima [1], the physical, chemical and structural properties and applications of this material have been investigated extensively [2–4]. The properties of CNTs are mostly dependent on the tubular diameter, doped atoms in the structure and chirality, which make their synthesis for the specific purposes difficult. A lot of studies have been done in the investigation of stable structures of non-carbon based nanotubes, among them boron-nitride nanotubes (BNNTs) have a great importance [5]. The stable tubular structure of BNNT was initially found by calculations [6] and later was successfully synthesized [7]. After this time, a large growing number of experimental and theoretical studies, specifically ab initio calculations on carbon-, silicon- and germanium substituted BN nanotubes have been performed on the electronic structures of the BNNTs [8–11]. The results show that C, Si and Ge replacements can induce spontaneous magnetization with different deformation in the nanotube [12].

At the present time, nuclear magnetic resonance (NMR) spectroscopy [13-14] is the best technique to study the electronic structure properties of materials. Doping of Chiral BNNTs by C, Si, Ge atoms changes their properties and so the interactions of the nanotube and foreign atoms or molecules. (see Fig. 1). In this work we studied the electronic structure properties, including bond lengths, bond angles, dipole moments (µ), energies, band gaps, and NMR parameters in the C, Si, Ge doped Chiral BNNTs structures.

a b c d e f g

2. Computational methods

All calculations were performed using Gaussian 98 computational package [15] with density functional theory (DFT) method using Becke’s three-parameter hybrid exchange functions with the correlation functions of Lee, Yang, Parr (B3LYP) [16,17] using 6-31G (d) basis set [18]. Previously it has been found that the calculated NMR parameters at the B3LYP and B3PW91 levels have a good agreement with the experiment [19]. It is shown that B3LYP gives reasonable and even accurate band gap values for nanotubes [19] so this function is chosen for band gap calculations.

In the present study, we considered a pristine (6,3) chiral BNNTs of diameter 6.6 Å and 10.1 Å length. This BNNT model consists of 42 Boron, 42 Nitrogen and 18 hydrogens (B42N42H18) B and N sites of this BNNT are doped by C, Si, Ge (see Fig. 1).

We have seven models, namely pristine (Fig. 1a), or with a B or N atom doped by C, i.e., the B-C-B or N-C-N model (Fig. 1b, c), doped by a Si atom, i.e., the B-Si-B or N-Si-N model (Fig. 1d, e), doped by a Ge atom, i.e., the B-Ge-B or N-Ge-N model (Fig. 1f, g). We investigated the influence of the C, Si, and Ge doping on the properties of the (6,3) Chiral BNNTs. The hydrogenated models of the pristine (6,3) Chiral BNNTs and the three atoms doped models of BNNTs consisted of 102 atoms with formulas of B42N42H18 (pristine), CB41N42H18 and CB42N41H18 (B-C-B or N-C-N model), SiB41N42H18 and SiB42N41H18 (B-Si-B or N-Si-N model), GeB41N42H18 and GeB42N41H18 (B-Ge-B or N-Ge-N model). The calculated CS tensors in the principal axis system (PAS) with the order of σ33 > σ22 > σ11 [20] for C, Si, and Ge doping for the investigated models of the (6,3) Chiral BNNTs were converted into measurable NMR parameters (isotropic chemical shielding (CSI) and anisotropic chemical shielding (CSA) parameters) using Eqs. (1) and (2) [23], summarized in Tables 3-6.

CSI(ppm)= (σ11+ σ22+ σ33) (1)

CSA(ppm)= σ33–(σ11+ σ22) (2)

For NQR parameters, computational calculations do not directly detect experimentally measurable NQR parameters, nuclear quadrupole coupling constant (CQ), and asymmetry parameter (). Therefore, Eqns. (3) and (4) are used to convert the calculated EFG (electric field gradient) tensors in the principal axis system (PAS) with the order of |qzz| > |qyy| > |qxx| to their proportional experimental parameters; CQ is the interaction energy of nuclear electric quadrupole moment (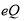) with the EFG tensors at the sites of quadrupole nuclei (Nuclei with nuclear spin angular momentum greater than >1/2), but the asymmetry parameter () is a measure of the EFG tensors, which describes the deviation from tubular symmetry at the sites of quadrupole nuclei. The standard Q value (Q (11B) = 40.59 mb) reported by Pyykkö [21] is used in Eq. (3). The NQR parameters of 11B nuclei for the investigated models of the (6,3) BNNTs are summarized in Table 7.

(3)

(4)

3. Results and discussion

3.1. Structures of the (6,3) Chiral BNNTs

The structural properties consisting of the B-N bond lengths, bond angles, dipole moments (µ), energies, and band gaps for the investigated models of the (6,3) Chiral BNNTs are given in Table 1 and Table 2. R1, R2, and R3 are B-X-B and N-X-N bond lengths (doped atom and its neighbors). α, β, and γ are B-X-B and N-X-N angles. There are Six forms of C, Si, Ge doped Chiral BNNTs for the (6,3) Chiral model.

These calculations indicated that the average of the (X = C, Si, Ge) bond lengths of the B-X-B and N-X-N models is larger than those the pristine models. The reason seems to be increasing of atomic radius going from carbon to Ge.

The bond angles produce some structural deformations that are responsible for deformation in structure by changing the doped atom size respect to carbon. For the B-X-B and N-X-N (X = C, Si, Ge) models, the diameter values are larger than those the pristine models. It has worth to be noted that the significant changes of geometries are just for those atoms placed in the nearest neighborhood of X atom and those of other atoms almost remained unchanged.

3.2. Energy band structure and density of states

Table2. Energy, LUMO, HOMO, LUMO-HOMO gap, dipole moment μ, and electronegativity (χ) of the studied structures at B3LYP/6-31G(d).

The total densities of states (DOS) of these tubes are presented in Fig. 2. As can be seen from Fig. 2, the calculated HOMO-LUMO gap (band gap) of the (6,3) Chiral BNNTs is 6.2 (eV) and the calculated band gaps of the C , Si , Ge doped models molecular orbital’s are 3.5,5.8 , 5.0 , 5.0 , 5.5 and 5.0 (eV) respectively (See Table 2). Doping of C, Si, and Ge in these tubes causes significant changes in the gaps of the DOS plots. In comparison with the pristine model, the band gaps of these models are reduced that increase their electrical conductance. These results indicated that the doping of C, Si, Ge atom by B, N atoms B-X-B and N-X-N model (X=C, Si, Ge) has more influence on the band gap of the Chiral BNNTs (see Table 2). By increasing atomic number and size polarizability increases that enhances dipole moment. Dipole moments (µ) of the C, Si, Ge doped Chiral BNNTs structures (Fig. 1) indicate slightly changes with respect to the pristine model.

3.3. NMR parameters of the (6,3) Chiral BNNTs

The NMR parameters for the investigated models of the (6,3) Chiral BNNTs are tabulated in Table 3, 4, 5 and Table 6. In the pristine model of the (6,3) Chiral BNNTs, there are 42 B atoms and 42 N atoms in the considered model and the NMR parameters are separated into five layers and six Columns, which means that the CS parameters for the atoms of each layer and Column have equivalent chemical environment and electrostatic properties. In Fig. 1b,c,d,e ,f,g the B and N atoms has been replaced by the C, Si, Ge atoms.

Table 3 Isotropic shielding parameters of the studied structures at B3LYP/6-31G(d) The calculated results in Table 3 indicate that doping C, Si, and Ge slightly changes the NMR parameters of the various B and N atoms in (Fig.1b–g) of the Si, Ge, C doped(6,3) Chiral SWBNNTs except for the N25 and N27 atoms for which the changes are significant. Because among the atoms of (Fig.1b–e) B–X model (X= C, Si, Ge), the N25 and N27 atoms are the nearest neighbors of the C, Si, and Ge atoms; hence, both the CSI and CSA parameters show the most significant changes due to the C, Si, Ge doping. Also, changes in the CSI parameters of the N10 and N12 atoms, which are the next nearest neighbors of the C, Si, Ge atoms, are also notable. There are differences between the properties of the electronic structures of C, Si, Ge atoms.

Comparison of the calculated NMR parameters in (Fig. 1b–g) indicates that the properties of the electronic structure of the Ge doped (6,3) Chiral SWBNNTs are more influenced than those of the Si–N model, where the N atom is doped by the Si atom. We studied the electronic energies of the models. The changes in the NMR parameter due to the C, Si, and Ge doping are more significant for the N–Si, N–Ge, N-C models with the pristine model.

3.2. NQR parameters

The 11B NQR parameters (ηQ and CQ) in the geometrically optimized SWBNNT models were calculated from the EFG tensors. The results are tabulated in Table 7. A quick look at the results reveals that the calculated NQR parameters are not similar for various nuclei; therefore, the electrostatic environment of BNNT is not equivalent in length in all BNNT models. Since, in contrast with CNTs, the ends of BNNTs are different, the NQR values decrease from each end to the opposite end of the chiral model. It was proved before that the end nuclei in the SW-BNNTs are crucial to their growth and also field emission properties [22, 23]. Since no experimental NQR data for BNNTs are available in the literature, the tables do not include any reference experimental data for the calculated results. B17 and B46 in all models have the largest CQ that states greater orientation of the EFG tensor eigenvalues along the z-axis of the electronic distribution at the sites of the 11B17 and 11B46 nuclei. The electrostatic environments of atom B17 and B46 are stronger than in the other layers along the length of the tube. The largest change in CQ is due to B46, located in the layer of doped atoms, because doping changes the geometrical parameters and hence the electronic behavior of atoms.

Table 8 The 11B NQR parametersThe highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) in the pristine, and C–X (X=B, N) models are plotted in Fig. 3. For the pristine model, HOMO and LUMO are uniformly distributed throughout the B–N bonds, whereas, in the C–X model (X=B, N) models, HOMO and LUMO are highly localized at the doped regions. (see Fig. 3) In comparison with the pristine model, band gaps of the C, Si, and Ge doped models increased their electrical conductance.

Conclusion

We studied the electronic structure properties including bond lengths, bond angles, dipole moments (μ), energies, band gaps, the NMR parameter of the six C, Si, Ge doped SWBNNTs models by means of DFT calculations. The calculated results indicated that the average Ge-B bond lengths of the Ge-N model are larger than those the pristine and the C–B, C–N, Si–B, Si-N and Ge-B models: Ge–N>Si–N>Ge–B>Si–B>C–N>Pure>C-B.

The values of dipole moments (μ) of the six C, Si, Ge doped SWBNNTs are Ge–N> Si–N> Ge–B> C–N> Pure> Si–B > C-B. In comparison with the pristine model, the band gaps of the six C, Si, Ge doped models are reduced and their electrical conductance increased as: C–B > Si–B = Si–N = Ge–N > Ge–B > C-N. The NMR values for the B and N atoms directly bound to the C, Si, and Ge in the C, Si, and Ge doped models are significantly changed. Comparison of the calculated NMR parameters in the X–B and X-N (X=C, Si, Ge) models shows that the properties of the electronic structure of the X-B doped (6,3) Chiral SWBNNTs are more influenced than X–N model in Fig. 1b–g. The electronic sites of the B and N atoms in X-N model have greater effects than X-B model in Fig. 1 in the C, Ge, and Si doping processes.

References

[1]S. Iijima, Single-shell carbon nanotubes of 1-nm diameter, Nature 354 (1991) 56.

[2]H. Terrones, F. Lopez-Urias, E. Muooz-Sandoval, J.A. Rodriguez-Manzo, A. Zamudio, A.L. Elias, M. Terrones, Magnetization of carbon-doped MgO nanotube, Solid State Sci. 8 (2006) 303.

[3]F. Moreau, R. Langlet, P.h. Lambin, P.P. Kuzhir, D.S. Bychanok, S.A. Maksimenko, Dielectric properties of a novel high absorbing onion-like-carbon based polymer composite, Solid State Sci. 11 (2009) 1752.

[4]R. Joshi, J. Engstler, P. Haridoss, J.J. Schneider, Formation of carbon nanotubes from a silicon carbide/carbon composite,Solid State Sci. 11 (2009) 422.

[5]A. Loiseau, F. Willaime, N. Demoncy, N. Schramcheko, G. Hug, C. Colliex, H. Pascard, Mathematical modeling for the simulation of heavy metal ions, Carbon 36 (1998) 743.

[6]X. Blase, A. Rubio, S.G. Louie, M.L. Cohen, Stability and band gap constancy of boron-nitride nanotubes, Eur. Phys. Lett. 28(1994) 335.

[7]N.G. Chopra, R.J. Luyken, K. Cherrey, V.H. Crespi, M.L. Cohen, S.G. Louie, A. Zettl, Boron-nitride nanotubes, Science 269 (1995) 966.

[8]L. Guo, R.N. Singh, Catalytic growth of boron nitride nanotubes using gas precursors, Physica E 41 (2009) 448.

[9]B. Fakrach, A. Rahmani, H. Chadli, K. Sbai, J.-L. Sauvajol, Raman spectrum of single-walled boron nitride nanotube, Physica E 41 (2009) 1800.

[10]M. Mirzaei, An electronic structure study of O-terminated zigzag BN nanotubes, Physica E 41 (2009) 883.

[11]M. Giahi, M. Mirzaei, Computational NQR study of a boron nitride nanocone, Z. Naturforsch. A 64 (2009) 251.

[12]J. Wu, W. Zhang, Chem. Phys. Lett. 457 (2008) 169.

[13]R. R. Zope, B.I. Dunlap, Phys. Rev. B. 72 (2005) 45439-6.

[14]F.A. Bovey, Nuclear Magnetic Resonance Spectroscopy, Academic Press, San Diego, 1988.

[15]M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheese- man, V.G. Zakrzewski, J.A. Montgomery Jr., R.E. Stratmann, J.C. Burant, S. Dapprich, J.M. Millam, A.D. Daniels, K.N. Kudin, M.C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G.A. Petersson, P.Y. Ayala, Q. Cui, K. Morokuma, D.K. Malick, A.D. Rabuck, K. Raghavachari, J.B. Foresman, J. Cioslowski, J.V. Ortiz, A.G. Baboul, B.B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R.L. Martin, D.J. Fox, T. Keith, M.A. Al-Laham, C.Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P.M.W. Gill, B. Johnson, W. Chen, M.W.Wong, J.L. Andres, C. Gonzalez, M. Head-Gordon, E.S. Replogle, J.A. Pople, GAUSSIAN 98, Gaussian, Inc., Pittsburgh, PA, 1998.

[16]A.D. Becke, J. Chem. Phys. 98 (1993) 5648-5652.

[17]C. Lee, W. Yang, R. G. Parr, Phys. Rev. B. 37 (1988) 785.

[18]G. A. Petersson and M. A. Al-Laham, J. Chem. Phys. 94, 6081 (1991).

[19]M. Mirzaei, N.L. Hadipour, J Phys Chem A. 110 (2006) 4833-4838.

[20]Y. Matsuda, J. Tahir-Kheli and W. A. Goddard, The Journal of Physical Chemistry letters 1 (2010) 2946.

[21]R.S.Drago,Physical Methods for Chemists,second ed. ,Saunders College, Florida, 1992.

[21]P. Pyykkö, Mol. Phys. 99 (2001) 1617.

[22] S. Hou, Z. Shen, J. Zhang, X. Zhao, Z. Xue, Chem. Phys. Lett. 393 (2004) 179.

[23] E. Bengu, L.D. Marks, Phys. Rev. Lett. 86 (2001) 2385.