Biochemical Kinetics: Enzyme Catalysis
| ✅ Paper Type: Free Essay | ✅ Subject: Chemistry |
| ✅ Wordcount: 1343 words | ✅ Published: 23 Sep 2019 |
Biochemical Kinetics: Enzyme Catalysis
Abstract
In this investigation we study a model for enzyme catalysis which is part of the wider field of biochemical kinetics. The catalysis reaction rate is modeled by the Michaelis-Menten equation – where the environment is the surrounding cell and the enzymes active site is the system. In this paper we mostly draw conclusions visually from graphs, varying the substrate concentration and paying most attention to the outer ranges where it is furthest from the Michaelis constant. Included is also a study of the effects on the rate of reaction of a metabolic pathway of different enzyme activators and inhibitors. We finish with a discussion of the limitations of the model and possible improvements to further optimise it.
Introduction
The definition of Biochemical kinetics is the study of the different movements of different organisms like the speed at which chemical reactions occur. An element of this is the modeling of an increased rate of chemical reactions known as enzyme catalysis. A key driver of these reactions is protein dynamics on metabolic pathways. The metabolic pathways are a series of chemical reactions occurring within a cell. It is key to understand that a catalyst is defined as “A substance that accelerates or causes a chemical reaction without itself (the catalyst) being affected.”
Most Biochemical reactions taking place in animals, plants and microorganisms are maintained by protein enzymes, however nuclei acids also have catalytic abilities, but little is known about enzymatic functioning of RNA. All chemical reactions have a minimum amount of energy (known as the activation energy) which needs to be reached before a reaction can occur. Enzymes lower this activation energy thus speeding up the rate of these chemical reactions. This process can be seen in figure 1 below.
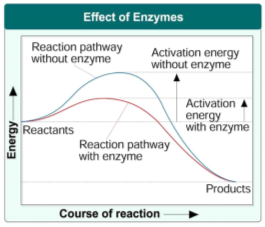
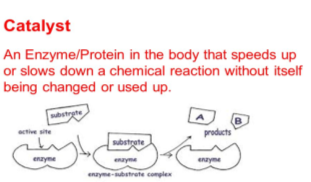
Figure 2 https://www.bing.com/images/search?view=detailV2&id=9D9FD2A610B207399ABBB58C51C28F65472C3755&thid=OIP.RpMgSn11biHfux7F47G1pAHaEK&mediaurl=http%3A%2F%2Fslideplayer.com%2F9319676%2F28%2Fimages%2F21%2FCatalyst%2BAn%2BEnzyme%252FProtein%2Bin%2Bthe%2Bbody%2B
Figure 1 Effects of Enzymes from http://coachhbio.blogspot.com/
Enzymes only react with one type of substance known as the substrate. The region of the enzymes that react with the substrate is the active site. The active site will only bind to that one type of substrate and undergoes a chemical reaction creating products and the unchanged enzyme will start again with other substrate molecules. This process can be seen in figure 2.
The products of these metabolic pathway reactions are split into two forms either catabolic or anabolic. Catabolic pathway reactions breakdown complex substances converting them to simpler compounds, which leads to the release of energy. Whereas anabolic pathway reactions are the opposite converting simple compounds to complex substances and require energy for this to occur. Enzyme rates of reactions can be increased or decreased by adding enzyme activators or inhibitors respectively. These activator molecules bind to the enzymes and alter by increasing their activity.
Enzymes activators trigger an increase in the substrate’s affinity (the attraction of the active site to the substrate) leading to increased catalytic activity. Two interesting types of inhibitors are competitive and noncompetitive inhibitors. If the inhibitor is competitive then the substrate and
inhibitor will resemble each other’s shape. A theory that explains why this process occurs is called the “lock-key theory”. If the affinity of the enzyme to the inhibitor is stronger than to the substrate, this will result in the inhibitor binding to the active site instead of the substrate. This will reduce the number of enzymes causing chemical reactions, reducing the rate of reactions. Whereas noncompetitive inhibitors will work to change the shape of the active sites so that the substrates cannot fit into the active sites, leading to enzymes which can’t break down the substrates. Therefore, enzymes natural rate of reactions is reduced.
Results of the Michaelis-Menten Model
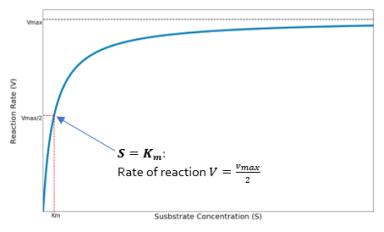
The rate of product formation for a metabolic pathway can be plotted as a function of the substrate concentration. In the Michaelis-Menten model the velocity of the reaction rate,
, forms a hyperbolic curve as the substrate concentration,
, increases. This can be seen below in Figure 1.
Figure 3 Rate of reaction for a metabolic pathway as a function of substrate concentration. Where VM is
and K is
(Michaelis constant)
(Region to the right of
):
In this situation the reaction rate,
, is directly proportional to the substrate concentration,
.
(Region to the left of
):
The reaction rate reaches the maximum,
, where saturation occurrs. There is a delay caused by waiting for an active site to become free before the next substrate can bind to an enzyme.
We can see that
is equal to the substrate concentration when the reaction rate is half the maximum rate,
. Therefore
is a measure of likeliness of an enzyme to bind to a substrate.
Inhibitors and Activators
In a metabolic pathway,
(the Michaelis constant), is affected by inhibitors and by activators which was spoken about in inthe troduction section, the impact can be seen in Figure 2 below.
Figure 4 The effect of inhibitors on reaction rate
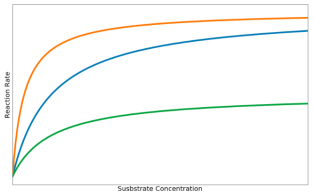 Competitive inhibitor: There is a gradual increase in reaction rate because competitive inhibitors are occupying only some of the enzyme’s active sites. As substrate concentration increases, the substrate molecules outnumber the inhibitors, so the reaction rate reaches the maximum.
Competitive inhibitor: There is a gradual increase in reaction rate because competitive inhibitors are occupying only some of the enzyme’s active sites. As substrate concentration increases, the substrate molecules outnumber the inhibitors, so the reaction rate reaches the maximum.
Noncompetitive inhibitor: Most enzyme molecules have become inactive, but some are unaffected by the inhibitors, so reaction rate remains low. An increase in substrate concentration does not increase the reaction rate due to the active site of the enzymes being denatured.
Normal enzyme: When no inhibitor is present, the rate of reaction against substrate concentration takes the form of the hyperbolic curve defined by the Michaelis-Menten equation.
Enzyme activators will increase the value of
but will have no effect on
regardless of the value
.
Conclusion and Outlook
The reactions between enzymes and substrates can be modeled using the Michaelis-Menten formula. Within this model, using the enzyme active site as the system and the surrounding cell as the environment, we expressed the rate of reaction in terms of the saturation rate and substrate concentration, along with the Michaelis constant and showed our results graphically. This can be taken further by also testing the effect of enzyme inhibitors and activators on the rate.
The consistency of the results is called into question whenever we know that the model does have limitations, however extensively it is used. Examples of this include:
- an equilibrium state is presumed throughout, where the enzyme-substrate complex remains constant. It is known that the equilibrium will in fact depend on the effect of enzyme inhibitors for example, and this effect is very difficult to accurately measure, making a simple amendment to the model difficult.
- in real circumstances there will be other molecules present at the site of the reaction and these molecules could affect how easily and efficiently the reaction can take place. This means that further variables would be needed to be added to the Michaelis-Menten formula to take this into account and make the model more robust.
- following on from the above point, in real circumstances there will be extra environmental conditions which may affect the optimality of the enzyme. Situations would include the temperature or pH around the reaction site, which in extreme cases could lead to the enzyme be permanently denatured over time. A way around this would be to have prechosen values for these parameters which are already known to create an optimal environment for each individual reaction.
Bibliography
https://www.dictionary.com/browse/catalyst
https://en.wikipedia.org/wiki/Enzyme_inhibitor
https://en.wikipedia.org/wiki/Enzyme_activator
http://www.worthington-biochem.com/introBiochem/inhibitors.html
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


