Applications of EME2 Asphalt

What is EME2 Asphalt

High modulus asphalt was developed in France in early 1990s and has been also introduced into other locations such as the United Kingdom and South Africa. Through a combination of high modulus and superior fatigue resistance, permanent deformation resistance, high durability and moisture resistance, the primary intention was to be able to reduce the thickness of a full depth asphalt pavement whilst still providing sound pavement performance. (Goktepe et al. 2006A. Bural Goktepe 2006; Dias et al. 2017)

The name EME is derived from the French Enrobé à module élevé, which is translates to “asphalt with elevated modulus” (Roads 2015). It consists of a hard-paving grade bitumen with a high binder content (approximately 6% by mass). Use of EME2 asphalt in other countries and the recent use in Australia has shown that the asphalt base layer thickness may be reduced by 20-30% leading to lower construction and maintenance costs. (Petho & Kidd 2015)

The first trial conducted in Australia was on 15 February 2014 at Cullen Avenue West, Eagle Farm, Queensland. The trial had shown that an EME2 base layer with a 30% reduction in thickness had a similar structural capacity compared to the control section using conventional asphalt (Petho & Kidd 2015). Five different designs were investigated in this trial and testing for various properties such as workability, flexural stiffness and fatigue was carried out

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

EME2 has a lower limit of 6% air void content in France but no upper limit. The Queensland trial achieved a 1% air void content and noted that if designed correctly, the low air void content does not introduce rutting issues.

Guidelines for mix design in France specifies that 0.2% additional binder increases fatigue resistance by 3µε. One of the designs utilised a 0.6% additional binder to improve fatigue characteristics however was found that voids filled with bitumen (VFB) values were over 90% and the stability of the mix posed a concern as it may fail in wheel tracking test.

A second trial was conducted in Victoria on the South Gippsland Highway which investigated the performance of EME2 using the same base layer thickness as opposed to reducing the thickness to achieve the same structural capacity as conventional asphalt demonstrated by the first trial in Queensland. Comparison of master curves for the Queensland and Victoria EME2 trials shows that the Victorian EME2 has slightly higher stiffness than the Queensland EME2. (Dias et al 2017) There is currently insufficient data cdocumented from the Victorian trial to allow comparison to the Queensland trial.

What is a stiffness master curve?

An asphalt mixture can be characterised by many characteristics which include the flexural stiffness, creep compliance, relaxation modulus and resilient modulus, however the dynamic modulus (|E*|) or stiffness of the AC mixture is used to determine the strains and displacement in a flexible pavement profile (Gopalakrishnan et al. 2014).

In pavement structural design, the stiffness of asphalt is typically a single value determined at a single temperature. As the asphalt structure is exposed to varying temperatures and loads throughout its life, this value may not be representative of the true behaviour of the material.

Dynamic modulus is a key material property used within mechanistic-empirical pavement design which determines the strains and displacements in the pavement structure under loading. The dynamic modulus of an asphalt mix is dependent of the temperature and the frequency at which the stress is applied.

The dynamic modulus is the absolute value of the complex modulus E* which is expressed in the equation below (Kasthurirangan Gopalakrishnan 2014):

$E^{*}=E_1+i{E}_2$

Where:

$\left|E^{*}\right|=\sqrt{E_1^2+E_2^2}$

|E*| can be determined physically by the ratio of the amplitude of the applied stress over the strain amplitude under the sinusoidal loading:

$\left|E^{*}\right|=\frac{{\sigma }_0}{{\epsilon }_0}$

The value of the dynamic modulus is highly dependent on the temperature and the loading rate.

Testing of dynamic modulus values is performed over a range of temperatures and loading frequencies as there is quite a considerable variety of array of temperature and loading frequencies at which an asphalt layer within a pavement structure will be exposed during its design life (Diaz and Archilla 2013). These values are used in the construction of a stiffness master curve using frequency-temperature or time-temperature superposition.

The master curve allows the effects of temperature and rate of loading to be known by providing the relationship between stiffness and reduced frequency using a sigmoidal function. It is noted that there are several different sigmoidal function equations used in literature (Gopalakrishnan et al. 2014).

A study has been conducted on the use of non-symmetric sigmoidal functions in master curve construction and showed that this may result in a master curve which is more representative of granular material behaviour.

Development of a master curve from FWD testing

A successful asset management system is able to make preventative and corrective decisions from a proper assessment or characterisation of the current status of the pavement profile modulus and be able to also be able to provide and accurate prediction of the future performance of the pavement structure.

This enables the local municipals the ability to appropriately allocate funds and resources for maintenance and rehabilitation. Non-destructive testing is a well-recognised method for evaluating the structural capacity and integrity of road pavements and is widely used by road authorities across the world. Pavement surface deflections, which are determined through a Falling Weight Deflectometer (FWD) have traditionally been used to indicate the structural capacity of the pavement profile in the aid of accurately providing rapid and repeatable in-situ characterising the structural condition of the existing pavement (Transportation 2008).

Throughout the FWD testing, an impulse load ranging from 6.7 to 156kN is applied to the pavement surface and associated surface deflections values are measured at different locations. Different FWD instruments produce different load pulse duration ranging between 20 and 60ms (Al-Khoury et al. 2001b). In the original methods of backcalculation, only peak values of the pulse and deflections at the measured locations are used to plot the deflection bowl curve. of Figure 1 illustrates the typical result of an FWD test. However several algorithms have been developed for converting the deflections obtained through the testing into pavement layer properties such as the elastic modulus of each of the structural layers (Garcia and Castro 2011).

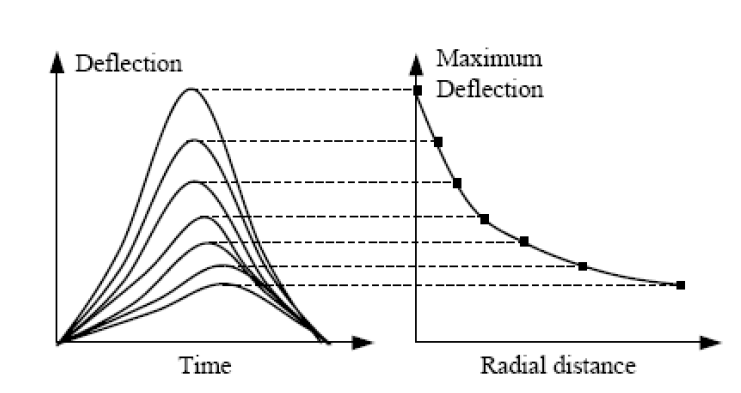
Figure 1 – Illustration of typical FWD deflection measurements ((Goktepe et al. 2006)

Backcalculation

Backcalculation or also known in scientific disciplines as parameter identification problems is an optimisation process to obtain inverse mapping of a known relationship established by discrete or continuous data points. In a pavement a pavement system, the backcalculation process is the numerical analysis of measured surface deflections from FWD testing in order to establish the estimated layer stiffness parameters, namely asphalt moduli.

Backcalculation is completed by matching the FWD load and deflections to those from a theoretical model by varying the pavement layer parameters, this is normally achieved via the layer modulus.

Available research material documents that numerous backcalculation techniques have been developed for pavement layer modulus as seen in Figure 2 below:

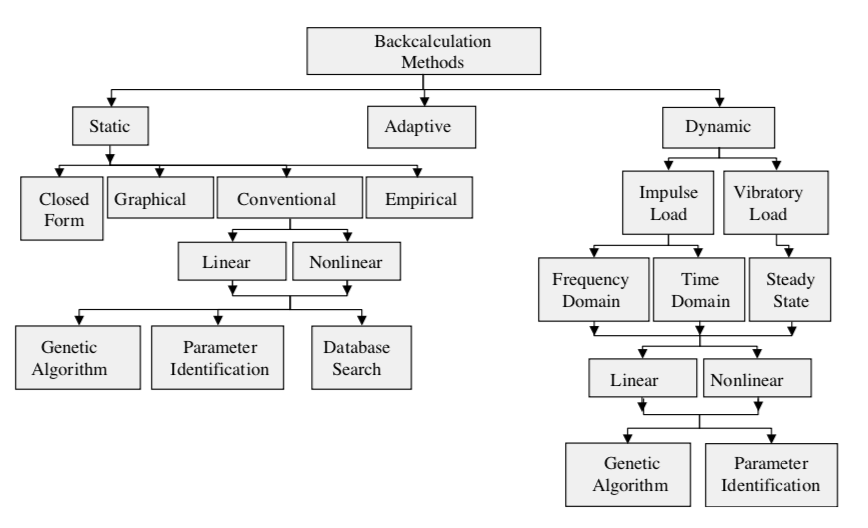
Figure 2 – Overview of backcalculation methods (Goktepe et al. 2006)

Static backcalculation procedure involves two calculation directions of analysis, namely forward and inverse. Using the assumed pavement layer moduli, the forward direction analysis is calculated through the theoretical deflections under the applied load. In the inverse direction of analysis, the measured deflections are compared to the theoretical deflections and an assumed modulus. The assumed modulus is fine-tuned through an iterative process until the theoretical and the measured deflection bowls seeming match.

Utilising this method of backcalculation does have its limitations. The loading is assumed to be static, whilst in reality, the loading from FWD is dynamic. Major cracks in the pavement or testing near a joint can cause the deflection data to depart drastically for the assumed conditions, also some pavement layers are too thin to be backcalculated in the pavement model however, thin layers only contribute a small portion to the overall deflection. Furthermore, temperature gradients exist in the pavement which can lead to modulus variation in asphalt layers and warping in concrete layers.  Viscoelastic pavement properties and dynamic effects, including inertia and damping can also affect the pavement response. The static backcalculation method neglects these effects and therefore less reflects the actual situation. These limitations can lead to erroneous results and caution should be applied (Gopalakrishnan et al. 2014).

The backcalculation procedures developed previously have been derived by solving the equilibrium equations under static conditions and only account for peak magnitude of the impact load and the peak deflection measured at different senor locations. This is commonly referred to as a deflection bowl. As these procedures are based on static conditions, they don’t allow for the simulation of the FWD loading and deflection as a function of time (Lee et al. 2017).

As FWD testing produces an impact load, thus producing dynamic effects, such as inertial and viscous effects and reflected waves could considerably affect these deflections. Dynamic methods have been studied by numerous researchers (Zaghloul and White 1993)

(Liang and Zeng 2002)    (Grenier and Konrad 2009)  (Al-Khoury et al. 2001)  (Al-Khoury et al. 2002) Of these forward methods most have adapted the analytical or semi-analytical approaches, however some have employed finite element or spectral element of numerical method (Gopalakrichnan et al. 2014).

The material properties that are affecting the dynamic response of a pavement are Poisson’s ratio ( $\nu$

), mass densities ( $\rho )$

, Young’s modulus (E), Complex modulus (G* or E*) and damping ratio ( $\beta )$

.

Time history data can also be fitted into the frequency domain or the time domain. In the frequency domain fitting, the deflection response times and load histories are converted by using the Fourier transformation into the frequency domain. Similarly, with the time domain fitting, the impulse load time histories should be transformed into the frequency domain data in order to input the available forward model into the frequency domain. This method requires finite integrations. However, (Al-Khoury et al. 2002) states that using the Fourier-Bessel series for the spatial domain and fast Fourier transforms alleviates the inconvenience of the numerical implementation of the finite integrals. 

The theory behind the viscoelasticity is not too dissimilar to the dynamic backcalculation methods where if one of the linear viscoelastic properties are knows, then the others can be calculated through numerical interconversion procedures. 

The backcalculation research completed by (Kutay et al. 2011) developed an algorithm to back calculate a layered viscoelastic forward solution for which they state is accurate and provides efficiencies due to the computations completed. However, this algorithm relied on information such as thickness of each layer, including asphalt, base and subbase, which notes that these are assumed to be known. It also required the modulus and the Poisson’s ratio of the layers beneath the asphalt layer. It notes in the report that these were assumed for the unbound layers’ modulus.

The development of dynamic backcalculation procedures definitely has its advantages as it considers the viscoelastic properties which provides for more precise results than a static procedure. However, the current dynamic backcalculation procedures have more complexity and require a far greater computational expense, additionally the uniqueness of the solution is not always guaranteed and depends on the number of unknown parameters and the correlation between these parameters. And due to the many observations that are made in the dynamic methodology, correlations between unknow parameters are usually low, which is not the case in the static approach as it uses a deflection bowl (Grenier and Konrad 2009) (Gopalakrishnan et al. 2014); (Wen and Li 2013)

Theoretical fatigue life model

Fatigue cracking is one of the major distresses in an asphalt pavement. It is also one of the most fundamental indices used in the pavement mechanistic-empirical pavement design and analysis is the fatigue life. Consequently, there has been a need to rational fatigue model to accurately describe fatigue behaviour of asphalt mixtures that can be used in mix and structural designs.

Optimisation of pavement structures and asphalt mix designs have been greatly assisted by studies conducted on a fatigue model which were completed under certain traffic and environmental conditions. There are numerous fatigue models that exist, that will predict the life of an asphalt pavement, however they are fundamentally based on empirical correlation of either in the field or in the laboratory.

As such these fatigue prediction models were developed based on the laboratory fatigue test and then they were calibrated by using observations of the field fatigue performance by adding a calibration factor. However, this can cause many discrepancies due to the behaviour between the field and laboratory conditions. In the study completed by J Yu et al 2012, they standardised the testing by using a four-point bending beam. This allowed them to conduct the test in both constant strain fatigue test, which is the repeated loading test for which the amplitude of the deformation of the beam specimen is maintained constant and constant stress fatigue test which is the repeated loading test where the amplitude of the stress of the beam specimen is maintained constant. This was completed until the cumulative load cycles reached a 50% reduction of the initial stiffness. It was noted that throughout the testing, the constant stress tests induced more fatigue damage than that testing of the constant strain. 

As part of their experimental design, standardisation of the constant strain and constant stress test modes. Following this, a sigmoid function was then developed to take into account the transition of the laboratory constant strain and constant stress mode to actual load mode of the field pavement.

(Li et al. 2012) questioned these previous fatigue models, as they are mostly phenomenological models, which directly correlate the fatigue life of the asphalt mixture with the initial pavement responses. Due to these models being dependent on either stress or strains, the model coefficients are strongly dependent on loading conditions, material types and test methods. Instead the authors recommended that a fatigue prediction model that is based on the dissipated energy ratio which has the ability to reasonably predict the fatigue lives of the various asphalt mixtures without changing the model coefficients. This model would also be independent of binder types, binder contents, strain levels and volumetric properties.

Crocodile cracking or bottom-up cracking has been documented and studied for decades and is the most well-known fatigue cracking for asphalt pavements. The research completed by  (Li et al. 2013) confirmed that the traditional strain-based fatigue model is not an effective model when compared to the dynamic modulus inclusion model. The researchers developed a new model called the critical strain-energy density model, which is defined by the area under the curve of the stress and horizontal strain up to peak stress in the indirect tensile test, which can be seen below in figure 3.

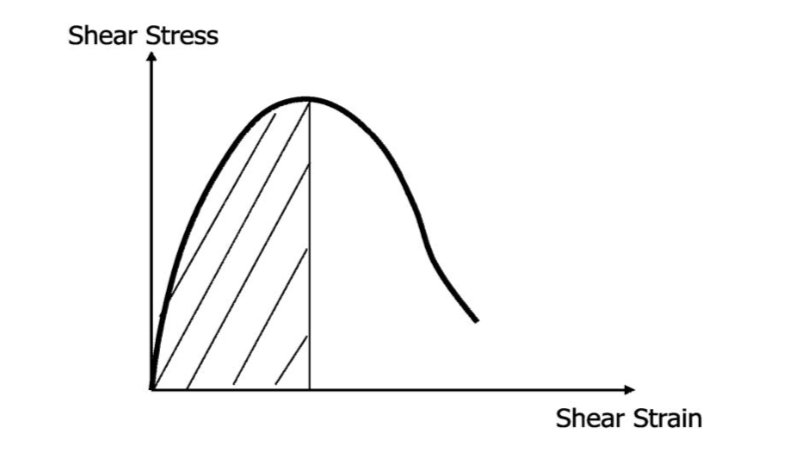
Figure 3 – Schematic diagram of critical strain-energy density (Wen and Li 2013)

The Illinois Department of Transportation

Once the pavement layer moduli are obtained, the compressive strain at the top of the base layer and the tensile strain at the bottom of the asphalt layer can be calculated. These numbers are then used to calculate the remaining number of equivalent single axle loads (ESAL’s) the pavement can withstand before reaching its breakpoint of rapidly accelerated deterioration. The traffic data can then be used to determine approximately the remaining pavement life before a pavement rehabilitation will be required. (Transportation 2008)

• A. Bural Goktepe, EA, A. Hilmi Lav 2006, ‘Advances in Backcalculating the Mechanical Properties of Flexible Pavements ‘, Advances in Engineering Software, vol. 37, pp. 421-31.
• Archilla, LGDaAR 2013, ‘From Testing to Design: An Easy Way to Use and Interpret the Results from the Asphalt Mixture Performance Tester (AMPT)’, International Journal of Pavement Research and Technology, vol. 6, no. 5, pp. 527-38.
• Castro, JARGaM 2011, ‘Analysis of the temperature influence on flexible pavement deflection’, Construction and Building Materials, vol. 25, pp. 3530-9.
• Hyung Suk Lee, DA, and Harold Von Quintus 2017, ‘Dynamic Backcalculation of Viscoelastic Asphalt Properties and Master Curve Construction’, Transportation Research Board, no. 2641, pp. 29-38.
• Kasthurirangan Gopalakrishnan, SK, Halil Ceylan, and Orhan Kaya 2014, Development of Asphalt Dynamic Modulus Master Curve Using Falling Weight Deflectometer Measurements, IHRB Project TR-659, IDo Transportation, Iowa Highway Research Board, Iowa State University.
• Konrad, SGaJ-M 2009, ‘Dynamic interpretation of falling weight deflectometer tests on flexible pavements uning the spectral element method: backcalculation’, Canada Journal of Civil Engineering, vol. 36, pp. 957-68.
• Laszlo Petho, AK 2015, EME2 mix design feasibility study for Brisbane City Council, Brisbane City Council
• Li, HWaX 2013, ‘Development of a Damage-Based Phenomenological Fatigue Model for Asphalt Pavements’, Journal of Materials in Civil Engineering, vol. 25, no. 8, pp. 1006-12.
• M. Emin Kutay, KCaLL 2011, ‘Backcalculation of Dynamic Modulus Mastercurve from Falling Weight Deflectometer Surface Deflections ‘, Journal of the Transportation Research Board, vol. 2227, pp. 87-96.
• Melissa Dias, DLP, Dr Erik Denneman and Andrew Beercroft 2017, High Modulus High Fatigue Resistance Asphalt (EME2) Technology Transfer, Austroads, Austroads.
• Qiang Li, HJLaTWK 2012, ‘A simple fatigue performance model of asphalt mixtures based on fracture energy’, Construction and Building Materials, vol. 27, pp. 605-11.
• R. Al-Khoury, AS, C. Kastergen and J. Blaauwendraad 2001a, ‘Spectral Element Technique for Efficent Paramter Identificationof Layered Media, Part 1: Forward Calculation’, International Journal of Solids and Structures, vol. 38, pp. 1605-23.
• R. Al-Khoury, AS, C. Kastergen and J. Blaauwendraad 2001b, ‘Spectral element technique for efficent parameter identification of layers media Part II: Inverse calculation’, International Journal of Solids and Structures, vol. 38, no. 8753, p. 8772.
• R. Al-Khoury, AS, C. Kastergen and J. Blaauwendraad 2002, ‘Spectral Element Technique for Efficient Parameter Identification of Layered Media, Part III: Viscoelastic Aspects’, International Journal of Solids and Structures, vol. 39, pp. 2189-201.
• Roads, DoTaM 2015, High Modulus Asphalt (EME2) Pavement Design TN142, Department of Transoort and Main Roads.
• S. M, ZaTDW 1993, ‘Use of a Three Dimensional Dynamic Finite Element Program for the Analysis of Flexible Pavement ‘, Transportation Research Board, vol. 1388, pp. 60-.
• Transportation, TDo 2008, Frequently Asked Questions about Falling Weight Deflectometer (FWD), Construction and Bridge Division.
• Zeng, RLaS 2002, ‘Efficient Computational Algorithms for Forward and Backward analysis of a Dynamic Pavement System’, Journal of Transportation Engineering, vol. 128, no. 4, pp. 366-74.