Work, Power and Energy Transfer – Questions and Answers
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 675 words | ✅ Published: 15 Sep 2017 |
Amy Harris
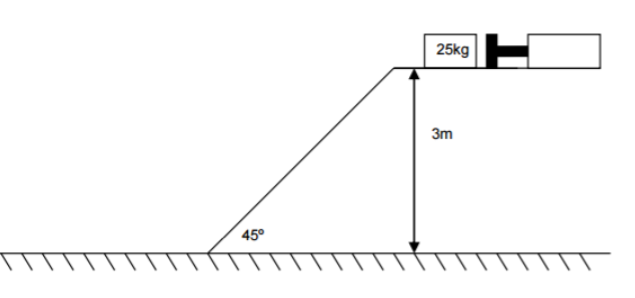 Task 1
Task 1
Packing cases of mass 25kg are to be pushed onto a ramp by use of a hydraulic ram as shown above. The coefficients of static and dynamic friction between the box and surface are 0.7 and 0.4 respectively. Assuming uniform acceleration at all stages.
Calculate:
a) The maximum force required in the ram to push the crate onto the slope with an acceleration of 0.25ms
b) The velocity of the crate as it leaves the top part of the ramp assuming this part of the movement takes 1 second.
c) The velocity of the crate at the bottom of the ramp
d) The distance travelled after leaving the ramp and continuing in a straight line (assume a smooth curve at the bottom of the slope).
e) The total time for the entire movement of the crate.

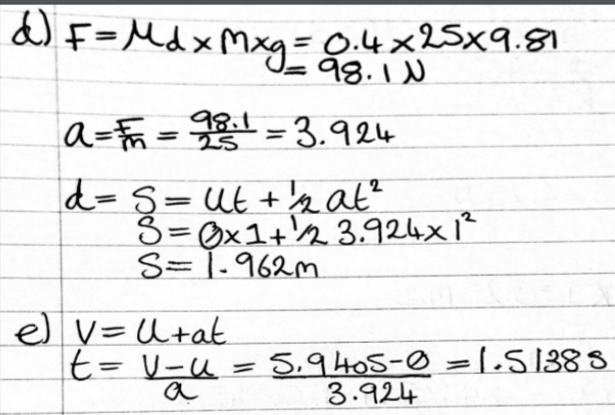
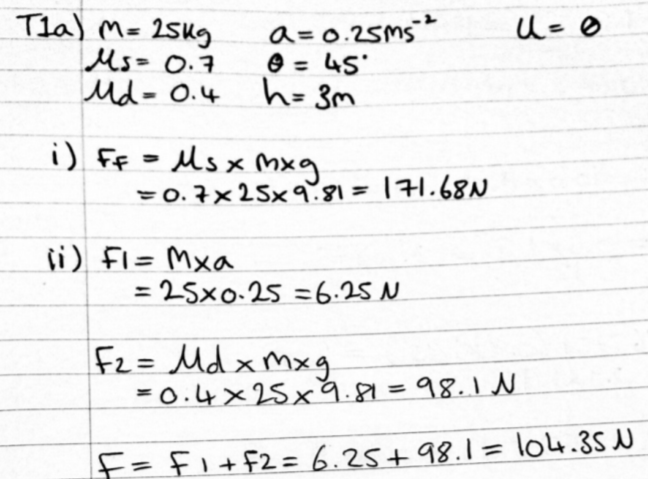
Corrections to Task 1:


 Task 2
Task 2
A pile driver hammer of mass 300kg is raised to a height of 3.5m before being released. If there is no rebound after impact with a pile of mass 500kg and the pile is driven 0.1m into the ground, Calculate:
a) The initial potential energy of the hammer before release.
b) The velocity of the hammer immediately before impact
c) The velocity of the hammer and pile immediately after impact
d) The deceleration of the pile assuming it is uniform
e) The ground resistance




Corrections to Task 2:

Task 3
Find the velocity of the hammer immediately before impact for the problem given in Q2 above using D’Alembert’s Principle and write a report comparing it with the conservation of energy method previously used.
How do the two methods differ and what were the discrepancies in the results?
The D’Alembert’s Principle can; in some parts, be very similar to the second law motion which Newton introduced. He thought that the law could be rewritten so that we can achieve the appearance of an equilibrium. This principle was made by Jean le Rond d’Alembert, he was a French mathematician in the 18th century. It is explained as reducing ‘a problem in dynamics to a problem in statics’ (The Editors of Encyclopaedia Britannica, 2016). I found that when referring to ‘the time derivatives of the momenta of the system‘ (Wikipedia, June 2016) D’Alembert’s principle shows this equation ‘F-ma=0′ (The Editors of Encyclopedia Britannica, 2016). I researched this formula and found that ‘F=ma'(classes R., no date) and newtons second law states that ‘F= mg’ (Kearsley, no date) This means that when no external force is present we may use the formula mg-ma=0. D’alemberts principle is different to the conservation of energy method as d’alemberts uses the equilibrium of forces when referring to a dynamic system and the conservation of energy method states that in a closed dynamic system the energy total equals zero. They may differ sometimes as they are dealing with different values to come out with the answer, also aspects such as human error when rounding comes into play as a small rounding error can sometimes affect the answer. The conservation of energy method is used more than the that of D’Alembert’s, perhaps because it is not often that a system is balanced completely which is when D’Alembert’s is used.
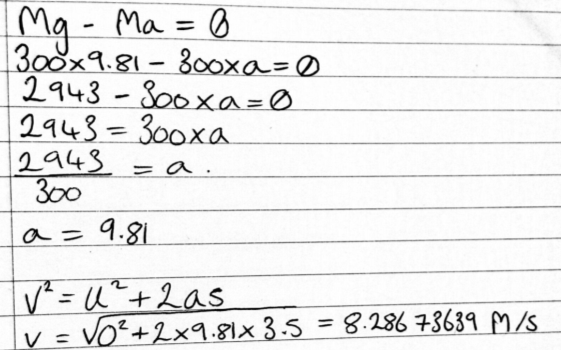
The answer I got is the same as I do with the other method, this shows that this method can be used to prove the answer found in task 2.
Bibliography
- The Editors of Encyclopaedia Britannica (20 July 1998) D’Alembert’s Principle [online] Available: https://www.britannica.com/science/dAlemberts-principle [Accessed 24/11/2016]
- The Editors of Encyclopædia Britannica (1998) D’Alembert’s principle | physics, in Encyclopædia Britannica [online] Available at: https://www.britannica.com/science/dAlemberts-principle [Accessed: 22/02/2017]
- Classes, R. (no date) D’alemberts Principle [online]Available at: http://kestrel.nmt.edu/~raymond/classes/ph321/notes/dalembert/dalembert.pdf [Accessed: 22/02/2017]
References:
- The Editors of Encyclopaedia Britannica (20 July 1998) D’Alembert’s Principle [online] Available: https://www.britannica.com/science/dAlemberts-principle[Accessed 24/11/2016]
- The Editors of Encyclopædia Britannica (1998) ‘D’Alembert’s principle | physics’, in Encyclopædia Britannica [online] Available at: https://www.britannica.com/science/dAlemberts-principle [Accessed: 22 February 2017]
- Kearsley (no date) Forces [online] Available at: http://www.mrkearsley.com/notes/physics-forces.pdf [Accessed: 2 March 2017]
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


