Spring Oscillation to Find the Spring Constant

Title: Using a spring oscillation to find the spring constant.

The aim of my report is to find the K (spring constant) by measuring the time of 10 complete oscillations with the range of mass of 0.05kg up to 0.3kg. It was been demonstrated by the lecturer and also the following instruction that I’ve been given.

This experiment will show and prove that with this method, we can calculate the spring constant by using the following formula,

In the meantime, we’ll be experience that we can get to find the spring constant, k, through this type method.

What is a spring constant?

Spring constant is a measure of stiffness or the ability to resist displacement under a load. It is denoted by K where;

The SI unit for the spring constant;

Nm-1

The spring constant tells u that it is the ratio of change of force with respect of deflection. So in other words, it is directly proportional to each other.

The spring constant can also be known as the force constant. It is a measure of the elasticity of the spring. In theory, the more its elastic value, the more the force you will need to act to extend the spring.

For example, a short spring has a higher spring constant than that of a long spring IF the other aspects or characteristics of it are the same or equal (thickness, material).

It will take you 10N to extend a short spring with 1cm.

To extend the long spring by the same amount, it would take less force, perhaps 5N for example.

Introduction on Hooke’s Law

Hooke’s law is the law of elasticity that was founded by the English scientist, Robert Hooke in the early 1660. It states that the extension or compression of a spring is directly proportional to the force exerted upon it.

Sometimes Hooke’s law is formulated asF=−kx where as in this expressionFis no longer the applied force but it was the equal and oppositely directed restoring force that causes elastic materials like springs to return to their original forms.

The law can also be expressed as the ratio of stress and strain. Stress is the force on unit areas within a material that develops as a result of the externally applied force while strain is the relative deformation produced by stress. For relatively small stresses, stress is proportional to strain. For particular expressions of Hooke’s law in this form, see bulk modulus; shear modulus; Young’s modulus.

Diagram of the apparatus used

Clear Description of the Method Used

As can be seen from the previous page, these are the description of the method by using the apparatus from the picture and as prepared by the lecturer.

1. At first, set up the apparatus which demonstrated by the lecturer.
2. Hang the first mass on the spring.
3. Allow the mass to oscillate up and down with a small amplitude and measure the time for ten complete oscillations.
4. Calculate the average from both of the time’s sets.
5. Find the time period T by dividing the average time by 10
6. Repeat all of the measuring of time by 5 more times with different masses which are from 0.05g.
7. Make a table regarding the results that you analysed.

Data Analysis Table

Graph of T² (y-axis) against m (x-axis)

Analysis & Discussion

The first thing that needed to do is get all the information of the data that I’ve collected from this experiment using the method and Hooke’s Law. Next step, all the result data were then arranged in a Microsoft Excel, which is to be completed by using the table.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

With the results that I’ve got from the method to measure k (speed constant) and for every each of the value from the “Blue dots”, (from the graph) was accurate enough to its original value. Although, most of my values are in the range of 2 N/m, it is acceptable.

Gradient

To find the gradient of the graph, firstly, we need two particular points which included 2 values from x-axis and 2 more values from y-axis.

The formula to find gradient is 

The equation of a line is 

For example, these values are from the graph:

1.  (0.06, 0.06)
2.  (0.29, 0.46)

SUBSTITUTE  = 1.74 (value of my gradient) (look at my graph)

Therefore it links with the equation of a line which is,

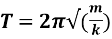
Like this,

Therefore the gradient is,

Thus, substitute the following gradient value with this to find k.

Value of k (speed constant)

Finding the value of k, from the equation,

The gradient that I found is 1.74N/m. Substitute it into the following gradient formula,

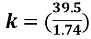
Total value of k = 22.7Nmˉ¹

Percentage Difference

(My total original value of spring constant divided by the value of spring constant)

Multiply by 100. × 100 = 60.3%

Accuracy and reliability

First thing that we should know is that the spring constant is depended on the displacement under a load. So by the result that I have calculated with the method and the formula given to find T² from the lecturer is not accurate as we would expected because of the formula that we should use is ” “.

The required unit for spring constant value is the acceleration of the free fall gravity and the displacement of the spring. Even though we can find the constant K by using the method from our lecturer, it will not be as accurate as the one with the formula ““, and with measuring time there’s a lot of miss accurate because of the possibility of human error.

We can also substitute into” “, however there is no value given for the length or displacement of the springs given, thus, giving us more uncertainties error.

Comment:

Reasons for Uncertainties

1. Amplitude is different from each of the results causing it not to be precise.
2. The disability of finding the missing length of the spring which is not constructed by the lecturer is very important to find the spring constant.
3. Spring constant cannot be invented because as the number of how much weight or force that we need to apply to make the spring extended by 1 metre and based on the spring function.
4. Due to the human error, the reaction of calculating time of the stopwatch will never be accurate.
5. The measurement of an angle from working out the oscillation is inaccurate.

Improvement for Uncertainties

1. Firstly, we need the value of the spring length which will be easier to be calculated and comparing the percentage difference between the method that I’ve used and the one with this improvement.
2. If there is a modern technology that can be invented that can measure the length of the spring when they stretch and to determine the time of oscillation with the creation of lasers to determine the period for each oscillation.
3. Need an instrument that can hold the pendulum before and after the 10 complete oscillations so that every each of the oscillation within both period (time and time 2) will be measured accurately.
4. In my honest opinion, the more accurate method to find the spring constant is to measure the spring’s displacement rather than using time as the unit to find k, spring constant, so we can now substitute the one we got previously to the formula

Referencing Lists

• Bray, A. Barbato, G. Levi, R. (1990). Theory and Practise of Force Measurement. San

Diego: Academic Press Limited. 52-53.

• Hosch, W.L. (2006). Hooke’s law Retrieved from http://www.britannica.com/EBchecked/topic/271336/Hookes-law

• Iris. (2009). what is spring constant? Retrieved from http://answers.yahoo.com/question/index?qid=20090902015640AAmDuLn

• Keller, J.F. (1993). Physics Classical and Modern (2nd ed.). McGraw-hill Inc. 331-350.