Spin Coherent State in Real Parameterization SU(4)

Coherent states in SU(4) of spin systems and calculate the Berry phase for qudit with spin 3/2 particle in SU(4) in quantum mechanics

Yadollah Farahmand^*, ZABIALAH HEIDARNEZHAD^**, Fatemeh Heidarnezhad^***,

Fatemeh Heydari^*** and Kh . Kh Muminov^*

Abstract

In this paper, we develop the formulation of the spin coherent state in real parameterization SU(4).we obtain Berry phase from Schrdinger equation. For vector states, basic kets are coherent states in real parameterization. Wecalculate Berry phase for qudit with spin S=3/2 in SU(3) group and Berry phase.

Key words: quantum mechanics, Schrdinger equation ,coherent state ,SU(n)group , Quadrupole moment , Berry phase.

Introduction

In 1984 Berry published a paper [1] which has until now deeply influenced the physical community. In mechanics (including classical mechanics as well as quantum mechanics), theGeometric phase, or the Pancharatnam-Berry phase (named after S. Pancharatnam and Sir Michael Berry), also known as the Pancharatnam phase or, more commonly, Berry phase[2], Therein he considers cyclic evolutions of systems under special conditions, namely adiabatic ones. He finds that an additional phase factor occursin contrast to the well-known dynamical phase factor. is a phase acquired over the course of a cycle, when the system is subjected to cyclic adiabatic processes, resulting from the geometrical properties of the parameter space of the Hamiltonian. Apart from quantum mechanics, it arises in a variety of other wave systems, such as classical optics [3].As a rule of thumb, it occurs when ever there are at least two parameters affecting a wave, in the vicinity of some sort of singularity or some sort of hole in the topology. In nonrelativistic quantum mechanics, the state of a system is described by the vector of the Hilbert space (the wave function) ∈ H which depends on time and some set of other variables depending on the considered problem. The evolution of a quantum system in time t is described by the Schrodinger equation

We consider a quantum system described by a Hamiltonian H that depends ona multidimensional real parameter R which parameterizes the environment of the system. The time evolution is described by the timedependent Schrodinger equation

We can choose at any instant a basis of eigen statesfor the Hamiltonian labelled by the quantum number n such that the eigen value equation is fulfilled

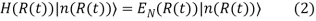
We assume that the energy spectrum of H is discrete, that the eigen values are not degenerated and that no level crossing occurs during the evolution. Suppose the environment and therefore R(t) is adiabatically varied, that means the changes happen slowly in time compared to the characteristic time scale of the system. The system starts in the n-the nergy eigen state

then according to the adiabatic theorem the system stays over the whole evolution in the n-the igen state of the instant Hamiltonian. But it is possible that the state gains some phase factor which does not affect the physical state. Therefore the state of the system can be written as

One would expect that this phase factor is identical with the dynamical phase factorwhich is the integral over the energy eigenvalues

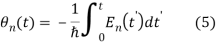
but it is not forbidden by the adiabatic theorem and the Schrodinger equation to add another term which is called the Berry phase [4-8]

We can determine this additional term by inserting the an sat z (4) together with equation (6) into the Schrodinger equation (1). This yields with the simplifying notation R ≡R(t)

After taking the inner product (which should be normalized) with we get

and after the integration

where we introduced the notation

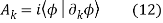
Then the total change in the phase of the wave function is equal to theintegra

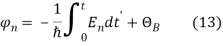
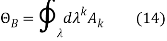
The respective local form of the curvature has only two nonzero components:

The expression for the Berry phase (14) can be rewritten as a surface integral of the components of the local curvature form. Using Stokes formulae, we obtain the following expression

where S is a surface in and are components of the local curvature form .[9]

Berrys phase for coherent state in SU(4) group for a spin particle (qudit)

We consider reference state as for a spin-3/2 particle (qudit) in SU(4) in nonrelativistic quantum mechanics. Coherent state in real parameter in this group is in the following form [10-12]

where |0i is reference state and

is Wigner function. Quadrupole moment is

Octupole moment is

If we insert all above calculation in coherent state, obtain:

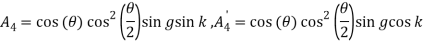
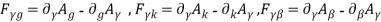
Discussion

Geometric phases are important in quantum physics and are now central to fault tolerant quantum computation. We have presented a detailed analysis of geometrical phase that can arise within general representations of coherent states in real parameterization in SU(4). Berry phase also change in similar method. We can continues this method to obtain Berry phase in SU(N) group, where N ≥ 5 . we can also obtain Berry phase from complex variable base ket, we conclusion that result in two different base ket is similar. Berry phase application in optic, magnetic resonance, molecular and atomic physics [13,14] .

References

[1] M. V. Berry, “Quantal phase factors accompanying adiabatic changes,”Proc.R. Soc. Lond. A 392 (1984) 45–57.

[2] S. Pancharatnam, Proc. Ind. Acad. Sci. A44, 247-262 (1956).

[3] M.V. Berry, J. Mod. Optics 34, 1401-1407 (1987).

[4] M. V. Berry. Quantal phase factors accompanying adiabatic changes. Proc.

Roy. Soc. London, A329(1802):45-57, (1984).

[5] J. J. Sakurai. Modern quantum mechanics, (1999).

[6] Yadollah Farahmand, Zabialah Heidarnezhad, Fatemeh Heidarnezhad, Kh Kh Muminov, Fatemeh Heydari, A Study of Quantum Information and Quantum Computers. Orient J Chem., Vol. 30 (2), Pg. 601-606 ( 2014)

[7] Yadollah Farahmand, Zabialah Heidarnezhad, Fatemeh Heidarnezhad, Fatemeh Heydari, Kh Kh Muminov, Presentation Quantum Computation Based on Many Level Quantum System and SU(n) Cohered States and Qubit, Qutrit and Qubit Using Nuclear Magnetic Resonance Technique and Nuclear Quadrupole Resonance. Chem Sci Trans.,vol 3(4), 1432-1440(2014)

[8] Yadollah Farahmand, Zabialah Heidarnezhad, Fatemeh Heidarnezhad, Fatemeh Heydari, Kh Kh Muminov,Seyedeh Zeinab Hoosseinirad, Presentation Entanglemen States and its Application in Quantum Computation. Orient J Chem., Vol. 30 (2), Pg. 821-826 ( 2014)

[9] M. O. Katanaev, arXiv:0909.0370v2 [math-ph] 18 Nov (2009).

[10] V.S. Ostrovskii, Sov. Phys. JETP 64(5), 999, (1986).

[11] Kh. O. Abdulloev, Kh. Kh. Muminov. Coherent states of SU(4) group in real parameterization and Hamiltonian equations of motion. Reports of Tajikistan Academy of science V.36, N6, I993 (in Russian).

[12] Kh. O. Abdulloev, Kh. Kh. Muminov. Accounting of quadrupole dynamics of magnets with spin . Proceedings of Tajikistan Academy of Sciences, N.1, 1994, P.P. 28-30 (in Russian).

[13] T. Bitter and D. Dubbers. Manifestation of berry,s topology phase in neutron spin rotation. Phys. Rev. Lett, 59:251-254, (1987).

[14] D. Suter, Gerard. C, Chingas, Robert. A, Harris and A. Pines, Molecular Phys, 1987, V. 61, NO. 6, 1327-1340.