Spacetime Structure Implications from Quantum Mechanics
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 2547 words | ✅ Published: 01 Feb 2018 |
Spacetime Structure Implications from Quantum Mechanics and Relativity
Abstract
Some idea proposed in the recent Penrose’s Conformal Cyclic Cosmology (CCC) is discussed in this paper. In CCC it is argued that the concept of time looses its meaning in a Universe filled solely with zero rest-mass particles (i.e. photons and gravitons). This particular idea is discussed, because at least conceptually it can have some implication on our understanding of spacetime and a role of rest-mass. Relativity was a great revolution in our understanding of space and time, sometimes leading to paradoxes. Quantum Mechanics introduced “quanta” of energy. It occurs that the existence of the minimum “quanta” of energy can has a strong implication on the spacetime structure. abstract should include at the max. 250 words. The abstract should give readers concise and correct information about the material of the article. It indicates what methodology you have used for your results and how you are concluding these results. The abstract should be restricted into a single paragraph with Times New Roman with Font Size 10, with proper justification.
Keywords: quantum mechanics; general relativity; conformal cyclic cosmology
Introduction
Einstein’s Relativity theory has been experimentally verified very thoroughly and also Quantum Mechanics predictions are experimentally very well checked. The philosophical or physical interpretation of mathematical equations of Relativity is commonly accepted. However Quantum Mechanics is a very good working operating tool, whereas the interpretation differs widely amongst physicist and philosophers (outlook of various interpretations can be found e.g. in [2]). Basing on the recent Penrose’s cosmological proposal [9] it seems that some implications to our understanding of spacetime can be derived from principles and as consequences of Relativity and Planck’s law. It can also lead to a specific interpretation of a wave function in Quantum Physics. The Penrose’s selected idea will be presented at first. Then some considerations influenced by this idea will be discussed.
Problems with time measurement
In [9] Penrose states that in a spacetime filled solely by photons and gravitons no clock can be built (Only the fact that rest-mass is zero is important. Therefore in the rest of this paper only photons will be discussed. Anywhere in the text when a photon is discussed it is important that it is a particle with zero rest-mass.). In order to have any clock a massive particle is needed. A stable massive particle “ticks” with the specific frequency (It can be derived by combining Planck’s formula  and Einstein’s formula
and Einstein’s formula 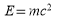 . Detailed discussion is in [9].).
. Detailed discussion is in [9].).
 (1) .
(1) .
So when there is no massive particles a spacetime looses its metric structure and only the conformal structure remains.
On the other hand the black hole evaporation process (known as Hawking radiation) [5] may lead the Universe to such a state in a very long time. Simply speaking if the Universe will be expanding (and therefore cooling) then after some time the background will be cooler than all black holes. Of course the infinite expansion is assumed.
There are however some objections, because there may be some matter left, not collapsed to black holes. E.g. some lonely massive particles can resist. Penrose discuses both possibilities: some highly hypothetical process of loosing mass in a very long period and implications of an event horizon. It is not a scope of this paper to discus it more thoroughly. Only to state that a spacetime filled only with zero rest–mass particles is physically interesting, reasonable and possible. Penrose argument that in such a spacetime no time measurement can be done (and only conformal structure remains) seems true [3, 11]. Briefly “one can dispense with the geodesics neither of test particles nor of light rays in measurement process” [6]. More discussion on this topic can be found e.g. in [10]. In this paper it is assumed that Penrose’s proposal is true and if spacetime is filled with zero rest-mass particles or massive particles which cannot influence each other due to event horizon then time cannot be measured in such a spacetime. Possible consequences of this statement will be discussed.
Proper time of a photon, the Observability Principle and tiling a spacetime
Let us consider a spacetime filled only with zero rest-mass particles. From Special Relativity it is known that any of such a particle “feels” no proper time. For example no time passes for a photon between its emission from the Sun and its absorbing on the Earth. Time passes e.g. for people on the Earth, but no time passes for a photon. Sticking to the Observability Principle, which means that anything which cannot be observed does also not exist [7, 8], one can say that for a photon both events take place at the same time (Because time difference between leaving the Sun and coming on the Earth, such as for the people on the Earth, does not exist for a photon and is not observed by a photon.). It means that no time passes in the Universe filled only by zero rest-mass particles just as Penrose concluded in [9]. For the sake of clarity such a Universe will be called a Penrose’s Universe further in this paper.

Fig. 1: To distinguish between different configurations time is needed. In case of no time (inability to measure time) one can say that all possible configurations happen at the same time. Or simply each particle is at the same time in all possible places.
It seems important to present some consideration here (which was not stated by Penrose). From the above paragraph it can be concluded that different configurations can be realised in the same time. Here a time is understood as an internal property of a Penrose’s Universe. The meaning of adjective internal will be clarified throughout the rest of this paper. Of course we are used to measure time for example by comparing configurations of objects (e.g. distance proportions between parts of them, etc.). When we see an egg on a table and next we see smashed egg on the same table we guess that a time has passed. In sake of clarity in a Universe filled with photons solely we should distinct between configurations (able to happen at the same internal time) and events (which happen one after another due to the order of the arrow of time). In a Penrose’s Universe configurations are possible, but events are excluded by the definitions.
So in a Penrose’s Universe each possible configuration takes place in the same (internal) time. Equivalently they just take place simultaneously. (If there is no time it can be said that everything happens at the same time.) If one considers all possible configurations in a Penrose’s Universe, one can equivalently say that each zero rest–mass particle is everywhere at the same (internal) time (Let us notice that we may omit internal because if it is assumed that nothing exists except a particular Penrose’s Universe then any other reference for some other “time” cannot exist.).
Of course the fact that a photon “feels” no time when passing from A to B – i.e. that it has zero proper time – does not imply that it is therefore everywhere in spacetime and, in particular, it does not mean that it is “simultaneously” on all possible paths between A and B. Indeed, in relativity theory, light moves on well-defined null geodesics. What I am trying to emhasise is that without massive particles it is impossible to discriminate these geodesics [3] and therefore (actually this is the crucial step) following the Observability Principle we identify all situations that are undistinguishable. It may be concluded that this is somehow similar to rather commonly agreed thought that the reality emerges only in relation to the results of measurements.

Fig. 2: In A there is no massive particle. In B there are some. Time exists internally in B. A is a tiny Penrose’s Universe without time (as far as no interaction with B happens). A (global) time for which we can treat A as Penrose’s Universe is measured in B, because in A no time exists. It means that on A+B there is a time.
Such a picture is not valid in our Universe because efficient clocks exist in it. The apparent contradiction occurs only because we imagine a Penrose’s Universe from the external point of view (experiencing the flow of the time). If we imagine that nothing exists except a Penrose’s Universe we would not have to use internal to describe time. Simply no device to measure time flow would exist.
Now let us think about a spacetime as a manifold (as in General Relativity). One living in the spacetime approximates the global structure of the whole manifold by observing his neighbourhood. However locally there is no “absolute time” as Relativity states. Consider now a small tiny part of the Universe (an open subset in the manifold). The Universe is filled by both zero and non zero rest-mass particles (as our Universe we live in). But locally we can find small parts of it which are filled solely by photons. We can treat each such a part as a Penrose’s Universe as far as no interaction with any massive particle takes place. It is due to previous considerations. We can say that no time passes inside such a part as far as no event takes place. It is understood that events take place in the global Universe. And by the event we mean here some act of interaction between a part being a Penrose’s Universe and a part of the global Universe possessing at least one non zero rest-mass particle. Then these two parts can be treated as one part (being then not a Penrose’s Universe). In other words let us find in our Universe as much as possible very small Penrose’s photon filled local Universes. These small Universes differ from Penrose’s one big Universe by the fact that they can be treated as such only as far as they do not interact with some massive part. The idea of tiling the spacetime manifold is sketched on pictures.

Fig. 3: An interaction happened from part B to part A. A is no longer a Penrose’s Universe.
Fig. 4: Such a timeless Universe cannot be divided into a massive parts and Penrose’s Universe parts. No matter how we would tile this Universe each component has no time.
In a Penrose’s Universe it is unclear how the different configurations (space–time paths) are to be defined. Indeed, just as there is no time measure, so there is no spatial measure (with which one can distinguish, for instance the distance between points on two different paths). Therefore due to the Observability Principle particles in such a universe are as if they were everywhere at the same time. What is needed to talk about any time order is an interaction with some massive particles. Only then e.g. before and after are sensible notions.
Discussion on the Double Slit Experiment
In the famous double–slit experiment a photon seems to pass through both slits at the same time. Therefore a wave function has been introduced, because a particle behave as if it were a wave. However if one tries to localise through which slit a particle actually passes, interference image is erased and a particle behaves as a corpuscle. Therefore one says about corpuscular-wave dualism. But due to considerations in previous paragraph one should also be able to say that a photon really passes through both slits (because no time passes for a photon, so two event take place for a photon at the same time). And what is called a collapse of a wave function is just a choosing of a particular path out of all possible. Such a measurement is however possible only if non zero rest-mass is involved. It is known that as a particle becomes more massive quantum properties are less clear and lighter particles behaves more like a waves (photons, electrons). The ability to measure time interval can also be seen from Eq. (1). In such an interpretation a wave function is not an abstract existence in observer mind. It is a physical being. But as such should somehow depend not only on a particle but also on a spacetime in which is considered.
Summarising Relativity Einstein once strongly criticised any physical concept which is “independent in its physical properties, having a physical effect, but not itself influenced by physical conditions” [4]. Just a proposed interpretation of a wave function should therefore be justified if this wave function interacts with spacetime.
Basing on General Relativity we know that the spacetime is influenced by gravitation. So the first simple test for the new interpretation is to check whether gravitation changes a wave function. Fortunately such an experiment was done. Firstly neutron beam was scattered into two beams: each influenced by the same gravitational field. Secondly the whole apparatus was placed in a way that after scattering the gravitational fields for the first beam and for the second beam were different. By examining the interference pattern it was observed that the quantum-mechanical phase shift of neutrons is caused by their interaction with Earth’s gravitational field [1]. One can then also speculate that the gravitational field influences a wave function.
It can be objected that the proposed explanation of quantum mechanics is contradicted by the conservation of the energy. A particle really going thorough all possible paths would do infinite work. It is not true in the proposed scheme. No procedure could measure such an energy, because those trips take places in a part of a spacetime where no useful time concept exists. If time is immeasurable then the particle can do the work needed to go through all possible paths. However immediately when a working clock is used, a particular path is localised an the energy conservation is saved. It can also be seen from this argument that the Feynman’s Path Integral approach is the most natural formulation of Quantum Mechanics.
Conclusions
The presented arguments lead to the specific interpretation of quantum mechanics. Conceptually the presented considerations show that one can find some guide towards Quantum Physics starting from Relativity and Planck’s law. Especially Feynman’s Path Integral Formulation emerges in nice way.
Some further implication to Cosmology occurs. The Universe filled solely with zero rest-mass particles should be treated as in a superposition state of all possible states. Occurrence of strictly positive masses not separated by event horizon would give the origin to time and states being in a superposition can be reduced to a particular state. It advocates the concept of the Universe wave function.
In a black hole singularity time stops and mass density is infinite as is known from Relativity. If one would look at a singularity from the presented point of view one could say that mass density is infinite only for external observer. Because only such an observer has a meaningful concept of time. Infinite density occurs as a consequence of localising all in-falling particles in a point. However as it was explained in the paper if time stops, all particles can occupy the same point in the same “time” (which exists only for external observer). A possibility of application of the presented scheme will be explored in the future research.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


