Scientific Analysis of Car Crash
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 2676 words | ✅ Published: 01 Feb 2018 |
|
Cars: Speed and Safety |
|
By Mitchell Leung |
Contents (Jump to)
Figure 2- selected intersection; Klumpp Road and Logan Road
Figure 3- Intersection with Measurements
Figure 7- Specifications of Car
Analysis of Car Accident if Driver of Mazda 3 did Nothing Wrong
Introduction
Speeding in Australia is a very common issue with deadly and fatal consequences. In Queensland in 2009, 75 fatalities were identified as being a result from speeding (Centre for Accident Research and Road Safety, 2011).
Speeding is when you drive above the maximum speed limit or you drive too fast for the weather, road or traffic conditions (Road and traffic authority of New South Wales, 2013).
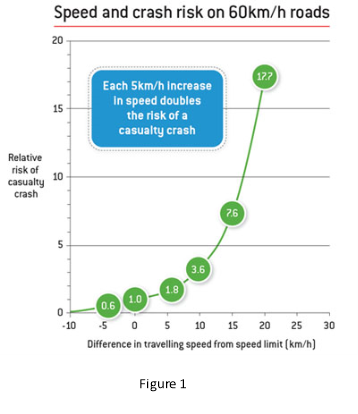 Driving over the speed limit has several implications. Some of them are, it increases the chance of being in a car crash, you have less time to react to a hazard and increases the severity of a car accident. The risk of a casualty crash approximately doubles with each 5km/h increase on a 60km/h speed limit road. The risk of a crash increases dramatically with each 10km/h increase on a 110km/h road. This is visibly seen in figure 1 (Government of South Australia, 2012).
Driving over the speed limit has several implications. Some of them are, it increases the chance of being in a car crash, you have less time to react to a hazard and increases the severity of a car accident. The risk of a casualty crash approximately doubles with each 5km/h increase on a 60km/h speed limit road. The risk of a crash increases dramatically with each 10km/h increase on a 110km/h road. This is visibly seen in figure 1 (Government of South Australia, 2012).
Speeding contributes to the increased risk of losing control of the vehicle. At higher speeds, vehicles become more difficult to manoeuvre around corners or curves and when trying to avoid a hazard. As the speed of the vehicle increases- so does the distance you travel while your brain is processing information and reacting to it. The average reaction time for most drivers to react to a hazard is 1.5 seconds. A driver who is fatigued, drunk or distracted (e.g. using a mobile phone) may take as long as three seconds to react to a hazard (Roads and Traffic Authority of New South Wales, 2013). Reaction time is how long a driver takes to see a hazard and the time it takes the brain to realise the danger and process a reaction to avoid the hazard (Roads and Traffic Authority of New South Wales, 2013).
During a car crash, there are several stages of accident. The first stage is vehicle’s collision with the object, weather it is a pole or tree etc. The first stage is when the car is travelling on the road, the ca will build up potential energy. The second stage is as the vehicle crushes on impact, it will absorb some of the kinetic energy released, but not all of it. The third stage is the human’s collision inside the vehicle. At the moment of impact, the occupants speed is the same as the vehicles speed. The passengers will continue to move until they come in contact with some part of the vehicle etc seatbelt.
Kinetic energy is a energy of motion. Objects moving such as a moving vehicle have kinetic energy. If the a car crashes into a wall at 5km/h, the wall won’t do much damage to the car. If the car hits a wall at 60km/h, the car would most likely be unrepairable. Kinetic energy is similar to potential energy. The more the vehicle weighs and the faster the vehicle is travelling the more kinetic energy it has.
Equations of Motion
Distance is a scalar quantity that refers to ‘how much ground an object has covered’ during its motion. (The Physics Classroom, 2014) An example of distance is if the car travels 15m from its original distance, the distance travelled is 15m. The formula for distance is speed x time.
Displacement is a vector quantity that refers to ‘how far out of place a object is’, it is the overall change in position. An example of displacement is when your car travels 150m from the starting spot and turns around and travels 150m (The Physics Classroom, 2014)
Acceleration is when the velocity of an object changes. Acceleration is the rate of change of velocity with time. (The Physics Hyper Text Book, 2014) An example of acceleration is at a set of red lights, a car is stopped, when the green light comes on, the car would accelerate in a positive direction. The formula for acceleration is  where a= acceleration, v= initial velocity (m/s), u=initial velocity (m/s) and t= time taken (s).
where a= acceleration, v= initial velocity (m/s), u=initial velocity (m/s) and t= time taken (s).
Velocity is a vector quantity that is the rate at which an object changes its position. (The Physics Classroom, 2014) An example of velocity is the current speed of a moving vehicle. For instance, the car is travelling along a road at a speed of 60km/h. The velocity of the car is 60km/h.
Braking distance is the distance a vehicle will travel from the point when it brakes to the time when it comes to a complete stop (Australian Academy of Science, 2003). The formula for braking distance is  , where V= initial velocity (km/h), μ=coefficient of friction (0.7) and g= acceleration due to gravity (9.8m/s2)
, where V= initial velocity (km/h), μ=coefficient of friction (0.7) and g= acceleration due to gravity (9.8m/s2)
Friction (Frictional Force) is a force that is exerted by a surface as a object moves across it or makes an effort to move across it. (The Physics Classroom, 2014) For example, when a car is stopped at a traffic light, there is no friction acting on the car. However, when the car is moving, friction is acting upon the car.
Momentum is a vector quantity that is a mass in motion. If the object has mass, then it will have momentum. (The Physics Classroom, 2014) An example of momentum is when a big truck and small car rolls down a hill both will engines off. The big truck will go down faster because it had a larger mass will gave it more momentum
Newton’s first law of motion states an object will stay at rest unless acted by an external force. In this context, the unbalanced force acting on the vehicles is the brakes.
Newton’s second law of motion states f=ma. F= force, m= mass, a= acceleration
Newton’s third law of motion states for every action, there is an equal and opposite reaction. For as the wheels on spin on a car, they grip the road and push backwards, since forces result from mutual interactions, the road must also be pushing the wheels forward.
Figure 2- selected intersection; Klumpp Road and Logan Road


Intersection Study
The intersection that will be used for the car crash is the intersection of Klumpp Road and Logan Road. The type of road that is used in that intersection is bitumen road. The type of traffic that would commonly use the road throughout the day is cars, trucks, buses, vans and motorcycles.
The speed limit of both Klumpp Road and Logan Road is both 60km/h
The crash will happen in the afternoon.
There are several environmental factors visible in the intersection. There are trees on the side of road A and H. The sun will be shining on the west side (right side) because the crash will happen in the afternoon. This means the driver of the mazda 3 will have the sun shining in the drivers eyes.
There are pedestrian walkways at every road in the intersection.











 Figure 3- Intersection with Measurements
Figure 3- Intersection with Measurements




 Figure 4- Before Crash
Figure 4- Before Crash











 Figure 5- First Impact
Figure 5- First Impact













 Figure 6- After Impact
Figure 6- After Impact



In this car accident, there will be two cars involved. The two cars chosen are a 2013 mazda 3 and a 2013 VW golf. The driver driving the mazda 3 on road g is speeding at a constant speed of 80km/h. The driver driving the VW golf accelerates when the traffic light turns green. The maximum speed the VW golf achieves is 30km/h. The driver of the mazda 3 slammed on the brakes when he saw the VW golf which is as soon as he passed the traffic light. The driver of the VW golf slammed on the brakes in the middle of the intersection.
Figure 7- Specifications of Car
|
VW Golf |
Mazda 3 |
|
|
Weight |
1351kg (Car Advice, 2014) |
1265kg (Car Advice, 2014) |
|
0-20km/h |
1.7s |
2.3s |
|
0-30km/h |
2.2s |
2.9s |
|
0-40km/h |
2.6s |
3.4s |
|
0-50km/h |
3s |
4s |
|
0-60km/h |
3.4s |
4.5s |
|
0-70km/h |
3.8s |
5s |
|
0-80km/h |
4.3s |
5.6s |
(Acceleration Times, 2014)
Analysis of the Car Accident
The VW golf accelerated from 0-30km/h in 2.2s (Acceleration times, 2014).
Convert km/h into m/s
30km/h=  -1
-1
ïœï€¸ï€®ï€³ï€³m/s-1 = 30km/h
Acceleration (VW golf)
The acceleration of the VW golf has to be calculated because the golf started from a standing start.
A= acceleration
V= initial velocity (8.3m/s-1)
U= final velocity (0m/s-1)
T= time taken (2.2s)

ïœThe VW Golf accelerated at a rate of 3.77m/s-2
Braking Distance (vw golf)

V= initial velocity (8.33m/s)
μ=coefficient of friction (0.7)
g= acceleration due to gravity (9.8m/s2)



d= 5.06m
ïœThe distance from when the driver slammed on the brakes in the middle of the intersection with ABS from 30km/h to the distance when the vw golf has come to a complete stop is 5.06m.
Acceleration (mazda 3)
Even though the mazda 3 does not start from a standing start, the acceleration still must be calculated to work out how fast the driver started accelerating on road g.
The mazda 3 accelerated from 0-80km/h in 5.8 seconds (acceleration times, 2014).
Convert km/h into m/s
80km/h =
Acceleration (mazda 3)
A= acceleration
V= initial velocity (22.22m/s-1)
U= final velocity (0m/s-1)
T= time taken (5.8s)



ïœThe mazda 3 accelerated at a rate of 3.83m/s-2
Braking Distance (mazda 3)

V= initial velocity (22.22m/s)
μ=coefficient of friction (0.7)
g= acceleration due to gravity (9.8m/s2)



d= 35.99m
ïœThe distance from when the driver slammed on the brakes when he passed the traffic lights with ABS from 80km/h to the distance when the mazda 3 has come to a complete stop is 35.99m.
Friction (VW golf)
FF=μFN
FF= force due to friction (Newtons)
μ=coefficient of friction between two surfaces (coefficient of friction between dry bitumen and rubber is 0.7)
FN= normal force (N)
First calculate FN=Fg= m x g
M= mass (1351kg)
G= acceleration of gravity (9.81 m/s2)
M x g= 1351 x 9.81= 13239.8N
ïœFN= 13239.8 N
FF=μFN= 0.7×13239.8 = 9267.86N
ïœThe amount of friction acting on the VW golf is 9267.86N
Friction (mazda 3)
FF=μFN
FF= force due to friction (Newtons)
μ=coefficient of friction between two surfaces (coefficient of friction between dry bitumen and rubber is 0.7)
FN= normal force (N)
First calculate FN=Fg= m x g
M= mass (1265kg)
G= acceleration of gravity (9.81 m/s2)
M x g= 1265 x 9.81= 12409.65
ïœFN= 12409.65
FF=μFN= 0.7 x 12409.65 = 8686.76N
ïœThe amount of friction acting on the mazda 3 is 8686.76N.
Momentum (mazda 3)
P=m x v
P= momentum (kg m/s-1)
M= mass (1265kg)
V= velocity (22.22m/s-1 west)
P= 1265 x 22.22
P= 28108.3
ïœThe mazda 3 has a momentum of 2.8×104 kg m/s-1 west
Momentum (vw golf)
P=m x v
P= momentum (kg m/s-1)
M= mass (1351 kg)
V= velocity (8.3m/s-1 north)
P= 1351 x 8.3
P= 11213.3
ïœThe vw golf has a momentum of 1.1×104 kg m/s-1 north
Velocity and angle of the collision between mazda 3 and vw golf
Mazda 3



Speed = 80km/h-1
 (22.22m/s-1)
(22.22m/s-1)
Mass= 1265kg
Vw golf
Speed= 30km/h-1
(8.33m/s-1)
Mass= 1391kg









The collision will occur at a right angle at the intersection of Logan and Klumpp roads.
X axis (mazda 3)
Law of conversation of momentum
Initial momentum= mass x speed = final momentum
Mass= 1265 kg
Speed= 22.22m/s-1
=1265 x 22.22
=28108.3kg m/s-1
Y axis (vw golf)
Law of conversation of momentum
Initial momentum= mass x speed = final momentum
Mass= 1351kg
Speed= 8.33m/s-1
=1351 x 8.33= 11253.83kg m/s-1
Add both of the momenta as vectors
 =px2+py2= 28108.32 + 11253.832
=px2+py2= 28108.32 + 11253.832
 = 790076528.9 + 126648689.7
= 790076528.9 + 126648689.7
 = 916725218.6
= 916725218.6
 =
= 
 = 30277.47kg m/s-1
= 30277.47kg m/s-1
30277.47kg m/s-1 is the final magnitude of the final momentum
Since the wreckage of the two cars has a combined mass of 2616kg, the speed of the wreckage can be found out by:


V= 11.57m/s-1
Convert m/s into km/h
11.571000 x 60 x 60
= 41.65 km/h-1
ïœThe speed of the wreckage is 41.65km/h
Find direction of wreckage
Use cos to find direction
cos= 
Cos θ= 
Cos θ= 0.4003
θ = cos-1 (0.4003)
θ= 66.403ï‚°
ïœThe wreckage of the two cars will move at a speed of 41.65km/h-1 at an angle of 66.403ï‚° to the direction of the mazda 3’s original motion.
Distance travelled of wreckage

D= distance the wreckage will slide before it stops (metres)
V= initial velocity (41.65km/h)
μ=coefficient of friction (0.7)
g= acceleration due to gravity (9.8m/s2)
Convert km/h into m/s
 11.57m/s
11.57m/s



d= 9.76m
ïœThe wreckage of the two cars travelled 9.76m
ïœThe wreckage of the crash travelled at 41.65km/h-1 at the angle of 66.403ï‚° to the direction of the mazda at the distance of 9.76m.
Analysis of Car Accident if Driver of Mazda 3 did Nothing Wrong
Braking distance if mazda 3 was not speeding.
Braking Distance (mazda 3)

D= distance the wreckage will slide before it stops (metres)
V= initial velocity (60km/h)
μ=coefficient of friction (0.7)
g= acceleration due to gravity (9.8m/s2)
Convert km/h into m/s
 16.66m/s
16.66m/s



d= 15.73m
ïœThe distance from when the driver slammed on the brakes with ABS from 30km/h to the distance when the mazda 3 has come to a complete stop is 15.73m.
From the distance when the driver slammed on the brakes to the distance where the car stopped, the car would not have run into the vw golf. However, the crash could have not occurred if the mazda 3 did not run the red light and followed the road rules.
Concluding Statement
The car accident scenario that was tested is a car (mazda 3) runs a red light at the speed of 80km/h-1 and then crashes into the vw golf who is following the road rules. The golf is travelling 30km/h-1.
The stimulus researched and the stimulus that was used in the car accident scenario is speeding.
The results that were found from the equations calculated earlier is the wreckage of the vehicle will move at a speed of 41.65km/h-1 at an angle of 66.403ï‚° to the direction of the mazda 3’s original motion with a distance of 7.58m.
In the future of cars, speed and safety, there has to be more emphasis and education to drivers so they are aware of the deadly consequences of speeding. Even driving 5km/h over the speed limit can double your chance of being involved in a car accident. Therefore the statement ‘every k over is a killer’ is a statement that is true and should not be ignored.
References
- Acceleration Times (2014).Mazda 3 2.2 CD acceleration times – AccelerationTimes.com. RetrievedMarch9, 2014, from http://www.accelerationtimes.com/models/mazda_3_22_cd
- Acceleration Times (2014).VW Golf GTI (MkVII) acceleration times – AccelerationTimes.com. RetrievedMarch9, 2014, from http://www.accelerationtimes.com/models/vw_golf_gti_mkvii
- Australian Academy of Science (2003, October).Fatal impact – the physics of speeding cars – Academy of Science. RetrievedFebruary11, 2014, from
http://www.science.org.au/nova/058/058key.html
- Car Advice (2014).Mazda 3 Price & Specs | CarAdvice. RetrievedMarch9, 2014, from http://www.caradvice.com.au/mazda/mazda3/price-specifications/
- Car Advice (2014).Volkswagen Golf Price & Specs | CarAdvice. RetrievedMarch9, 2014, from http://www.caradvice.com.au/volkswagen/golf/price-specifications/
- Centre for Accident Research and Road Safety (2011, August).State of the Road. RetrievedFebruary9, 2014, from http://www.police.qld.gov.au/Resources/Internet/news%20and%20alerts/campaigns/fatalfive/documents/speeding_fs.pdf
- Government of South Australia (2012, October 8).Road Safety : Speed facts. RetrievedFebruary17, 2014, from http://www.dpti.sa.gov.au/roadsafety/safer_speeds/speed_facts
- Nice ,K. (2014).HowStuffWorks “How Force, Power, Torque and Energy Work”. RetrievedMarch6, 2014, from http://auto.howstuffworks.com/auto-parts/towing/towing-capacity/information/fpte9.htm
- Quick Tip Science (2013, May 22). Stopping Distance Formula [Video file]. Retrieved from http://www.youtube.com/watch?v=oLPgNkuzw8M
- Roads and Traffic Authority of New South Wales (2013, July 11).Speeding- Did you know? RetrievedFebruary11, 2014, from http://www.rms.nsw.gov.au/saferroadsnsw/speeding_and_crashes.pdf
- Stelzer,T., Madden ,D., Lindsay ,I., Parsons ,D., & Gaze,T. (2007). Cars- Speed and Safety. InHeinemann Queensland science project, physics: A contextual approach(pp.47-69). Port Melbourne, Victoria: Pearson Education Australia.
- Study Physics California (n.d.).Lesson 20: Friction. RetrievedFebruary16, 2014, from http://www.studyphysics.ca/newnotes/20/unit01_kinematicsdynamics/chp05_forces/lesson20.htm
- Physics Classroom (2014).Distance and Displacement. RetrievedMarch12, 2014, from
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal







