Physics of Roller Coasters
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 2830 words | ✅ Published: 11 Sep 2017 |



Rollercoaster
Rollercoasters are amusement rides specifically designed to thrill and excite the riders. They utilize the laws of physics to give the best, safest possible experience to the riders (Merriam-Webster.com, 2016). Most rollercoasters consist of high speeds, loops, banked turns and hills reaching extreme heights. In the following amateur rollercoaster design, all these aspects will be broken down and the physics of each of these will be thoroughly examined.
In the following simple rollercoaster design, each part of the rollercoaster will be examined to find the forces that are acting upon it. Each part will then be evaluated and assessed.
Parts of Rollercoaster
Carts and Harnesses
Safety Procedures
Part A: Uphill slope of First Hill
Part B: Downhill of First Hill
Part C: Uphill Slope Second Hill
Part D: Downhill Second Hill
Part E: Elliptical Loop
Part F: Banked Turn 1
Part G: Bank Turn 2
Part F: End
Carts and Harnesses
One thing that is essential to any rollercoaster is a safe cart and suitable harness. Without these, the rollercoaster cannot be ridden. The carts that will be used in the rollercoasater are:
The seats and harnesses that will be used are the following:
 This seat was chosen because from experience, it is the most comfortable and allows for the rider to feel the maximum enjoyment of the ride without being to constrained. It allows for the arms to move more freely, and the legs to be free.
This seat was chosen because from experience, it is the most comfortable and allows for the rider to feel the maximum enjoyment of the ride without being to constrained. It allows for the arms to move more freely, and the legs to be free.
Safety Procedures
 Entering the queue for the ride, there will be a safety sign at the beginning detailing what isn’t permitted on the ride. There will also be a height restriction, where the rider must be above 110cm tall. There will also be a place provided for the riders to place any loose belongings. When the riders are seated, the harnesses will come down, and the staff member on duty will come around to every seat and check if the harnesses are down and safely secured. After all this has been done, the ride will then commence.
Entering the queue for the ride, there will be a safety sign at the beginning detailing what isn’t permitted on the ride. There will also be a height restriction, where the rider must be above 110cm tall. There will also be a place provided for the riders to place any loose belongings. When the riders are seated, the harnesses will come down, and the staff member on duty will come around to every seat and check if the harnesses are down and safely secured. After all this has been done, the ride will then commence.
Section A: Uphill Slope of First Hill
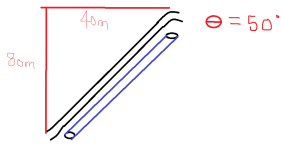 In the first hill, a chain system will be used to pull the cart to the top of the hill. This is used as there is not enough energy currently acting on the cart to force it up the hill. In this part of the rollercoaster, the energy needed to carry the cart to the top and the power needed has to be found. This will then determine what motor needs to be used.
In the first hill, a chain system will be used to pull the cart to the top of the hill. This is used as there is not enough energy currently acting on the cart to force it up the hill. In this part of the rollercoaster, the energy needed to carry the cart to the top and the power needed has to be found. This will then determine what motor needs to be used.
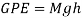
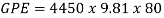
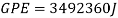
 This Energy can then be used to calculate how much energy will get lost to friction, which shows the efficiency of the first hill. It can be found using the following equation:
This Energy can then be used to calculate how much energy will get lost to friction, which shows the efficiency of the first hill. It can be found using the following equation:
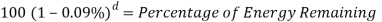
To find (d), which is the length of the track, Pythagoras will be used.
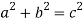
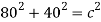
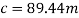
Now the percentage of energy remaining can be calculated
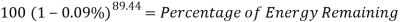
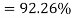
This percentage shows how much energy is left from the starting energy, and also shows that 8% of the energy was used to get up the hill and got lost through friction and sound.
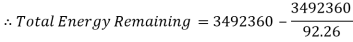
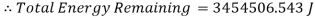
Now, in order to find the power, the time the energy is used for must be found. This is possible because the velocity and the displacement are already known. Assume that the velocity of the cart going uphill is 3.5meters per second.
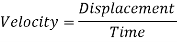

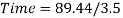
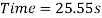
Now that the time has been found, power can be calculated.
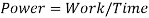
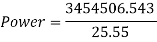
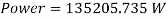
This can then be converted to Kilowatts, which is 135.2kw. Therefore, a motor that can use at least 136kw of power is needed to power the chain to carry the cart to the top of the hill. The TECO MAX-E3-H66 TEFC Motor (Teco.com, 2016) has a maximum power output of 185kw. This can then be used to calculate the efficiency of the motor.
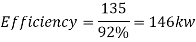
This shows that when the motor is outputting 135kw, it is using 146kw of power.
Evaluation and Conclusion
The first hill is designed to be very high, so as to get more GPE once at the top, and to either thrill, or scare the riders. The ascension to the top of the hill is slow so it can build up either fear and tension, or excitement between the riders. From experience at Dreamworld, height was a major thrill factor in any of the rides that were there. The higher the ride went to. Like the Giant Drop (Dreamworld.com, 2016), the more people would be scared or excited. The experiences felt on rides like the Giant Drop was one of the major factors contributing to the design of the uphill slope.
Part B: Downhill Slope of First Hill

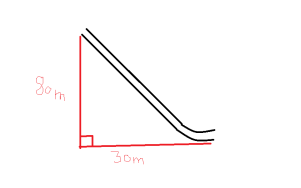 This is where the chain will stop carrying the cart. At the beginning of the slope, the GPE will be at its max. From now on, the rest of the ride will be depending on the energy and momentum of this descent. The energies and the forces of this part of the ride will need to be found.
This is where the chain will stop carrying the cart. At the beginning of the slope, the GPE will be at its max. From now on, the rest of the ride will be depending on the energy and momentum of this descent. The energies and the forces of this part of the ride will need to be found.
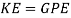
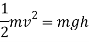
Wind resistance and friction also have to be taken into account. This would then change the above formula into:
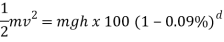
In order to find the length (d) of the track, pythagoras has to be used.
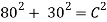
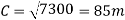
Now this information can be used to find the velocity.
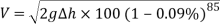
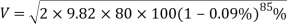
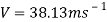
From these calculations, the tension felt at the curve at the bottom of the hill can be identified. For this equation, assume that the radius of the curve is 10m.
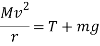
Rearrange to make T the subject.
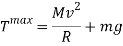
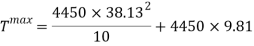
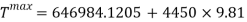
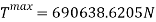
This is the maximum tension felt throughout the duration of the curve of the slope. From this equation, the acceleration can be found, which then can be used to find out the amount of G’s the riders will be experiencing. Since tension is a force, the force equation can be used to find the acceleration of the cart going into the slope.
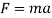
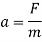
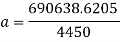
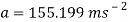
To find the Gs felt by the riders, the acceleration is divided by gravity.
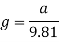
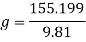
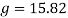
The g’s that the riders will experience at the bottom of this slope will be 15.82g’s. The average human body can only handle up to at least 8 g’s at the maximum before passing out, or worse (RollercoasterPhysics, 2015). In order for the amount of g’s to be lessened, the radius of the bend has to be increased. It will be increased to 40m.
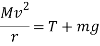
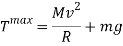
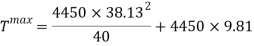
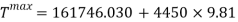
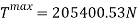
The acceleration can now be found:
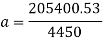
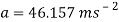
To find the g’s experienced:
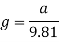
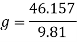
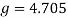
This is a much safer and suitable radius for the curve, as it lessens the amount of g’s felt by the riders to a safe level of only 4.7g’s.
To find the time it takes for the cart to go down the slope, the following equations, which are Newton’s Equations of Motion can be used:
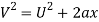
V=Final Velocity
U=Initial Velocity
A=Acceleration
X=length of track
Rearrange to make ‘a’ the subject:
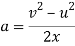
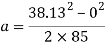
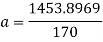
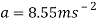
From the acceleration that was just found, it can be substituted into another one of Newton’s equations of Motion to find out the time it takes for the cart to go down the track.
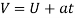
Rearrange to make’t’the subject.
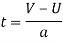
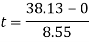
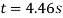
As shown in the calculations above, it would take approximately 4.46 seconds for the cart to reach the bottom of the hill.
Evaluation and Conclusion
In this part of the ride, the cart will from now on be relying on the GPE it has gained at the top of the hill to make it move along the rest of the track. At the bottom of the slope, I have chosen the curve bend to make it as safe as possible for the cart to transition from the downhill slope to the straighter, flatter part of the track until it gets to the next part of the track. In my calculations, I realized that the initial radius I had for the track (10m) was too small, which had increased the amount of g force exerted on the rider to a dangerous level of 15g’s. To fix this, the radius of the curve had to be increased, which would in turn decrease the g force felt by the riders. I increased it to 40m, which made the g force go down to a safer 4g’s.
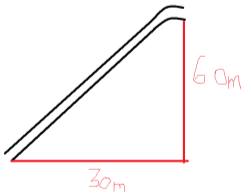 Part C: UpHill Slope Second Hill
Part C: UpHill Slope Second Hill
This is the second hill of the rollercoaster. It will be smaller than the first hill because there is no external factors that are helping the cart up the hill this time. The cart is only relying on the momentum and energy gathered from the first hill to carry it to the top of the second hill. There will be at least 10m of track between the end of the first hill to the beginning if the second hill.
 To find the length of the track, Pythagoras has to be used.
To find the length of the track, Pythagoras has to be used.
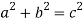
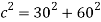
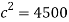
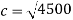
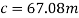
Now to find the energy acting on the cart on the track.
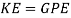
In order to find the energy at the top, the GPE has to be calculated.
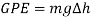
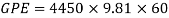
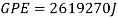
Now to find the KE. Energy lost due to friction will also be taken into account.
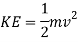
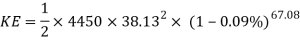
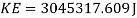
Since the cart is going uphill, the KE is going to be transferred to GPE, however since the hill is not high enough for all the KE to be transferred into GPE, there will be some leftover KE at the peak of the track (bbc.co.uk, 2016). This can be calculated with the following formula.
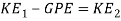
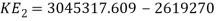
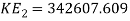
In order to find the velocity at the top of the hill, the KE formula will be rearranged to make ‘v’ the subject.
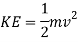
Rearranged to:
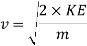
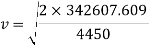
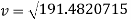
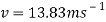
The velocity at the top of the hill will be 13.83 meters per second. The next thing to find is the time it will take for the cart to reach the top of this section. To do this, the acceleration must first be found.
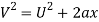
Rearrange to make ‘a’ the subject
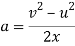
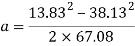
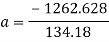
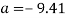
The acceleration is a negative number because as it is going uphill, it is actually decelerating, so the acceleration value should become a negative number. With this information, the time it takes for the cart to travel up the track can be found.
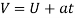
Rearrange to make’t’the subject.
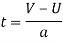
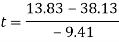
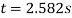
This is how much time it takes for the cart to travel to the top of the hill.
Evaluation and Conclusion
In this section of the ride, the riders will be going from a descent straight to another ascension. At the start of the slope, at the bottom, the riders would feel heavier due to the increase of G’s, but as they go up the slope, they will get that sinking feeling in their stomachs, similar to when you are driving and go down a small hill on the road and go back up almost immediately. This was included in the ride because at Dreamworld, there was a ride named the Claw (Dreamworld.com, 2016) that had this feeling. It swung in a pendulum motion, making the riders feel heavier at the bottom of the swing, and brought the riders up to the top, causing the riders to feel lighter and have that sinking feeling as they were going up. Another thing that the riders will feel on this part of the ride will be apparent weightlessness at the top of the slope. This was also felt on the Claw, at the peak of each swing. The riders will be feeling apparent weightlessness because as they go over the crest of the hill, they will be accelerating at the acceleration of gravity (Hyperphysics.edu, n.d). Another thing the riders will experience on this part of the ride is a negative ‘g’. When the riders are going up the hill, they are decelerating at -9.41m/s, which is almost directly opposite to the acceleration due to gravity, which is 9.81m/s. Anything over three negative G’s is very dangerous and harmful to the human body as it could cause blood vessels to erupt due to blood being overloaded in the head, and can also cause loss of consciousness (Ehow.com, 2016). On this however, the riders are only experiencing one negative G. This will give the riders apparent weightlessness as they are going to the top (Howitworksdaily.com, 2016). Internally, all the blood will be moving slower than the rest of the body due to inertia (Howitworksdaily.com, 2016), which is why they will be feeling apparent weightlessness. Overall, this section of the ride is safe and will provide the riders with several thrilling experiences.
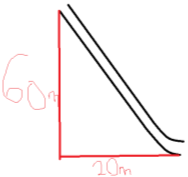 Part D: Downhill Slope Second Hill
Part D: Downhill Slope Second Hill
 This Downhill slope is very similar to the previous one, with the only differences being that it has different heights and lengths. The equations for solving this part of the ride will be similar to the previous downhill slope.
This Downhill slope is very similar to the previous one, with the only differences being that it has different heights and lengths. The equations for solving this part of the ride will be similar to the previous downhill slope.
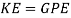
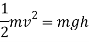
In order to find the velocity, the above equation will be rearranged to:
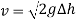
There will be some energy loss due to friction, which will change the previous formula into:
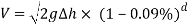
To find’d’, which is the length of the track, Pythagoras must be used.
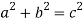
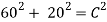
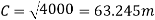
This can then be substituted into the formula to find the velocity of the cart travelling down the track.
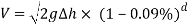
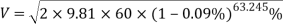
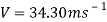
Since there is a curve at the bottom of the slope, the G force felt by the passengers must be calculated. In order to find the G force, the acceleration on the curve must be found. It can be found using the formula used to calculate force.
Rearrange to make ‘a’ the subject.
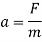
But, in order to use this formula to find the acceleration, the force acting on the curve must be found. Using the following formula, the tension, which is a force, can be found.
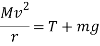
Rearrange to make T the subject.
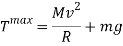
Based on previous calculations, the radius of the curve must be big in order for the G force to be at a safe level.
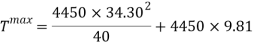
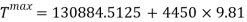
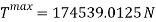
Now the acceleration can be found.
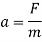
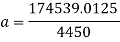
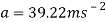
Using this, the G force can now be calculated.
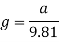
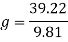
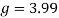
This is a suitable level of G’s as it is within the safe levels.
Now to find the time it takes for the cart to travel down the hill. Using Newtons Equations of Motion, this can be achieved. To find the time it takes for the cart to travel down the hill, the acceleration of the cart going down the hill must be found.
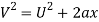
Rearrange to make ‘a’ the subject.
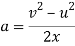
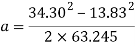
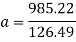
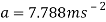
Now that the acceleration of the cart travelling downhill has been found, it can be substituted into another one of Newtons Equations of Motion to find the time it takes for the cart to travel downhill.
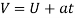
Rearrange to make’t’the subject.
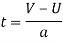
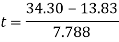
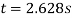
This shows that the cart spends 2 seconds to travel down the slope.
Evaluation and Conclusion
This hill is not as extreme as the previous one, as the calculations show, but will still provide a thrill factor to the riders. It is very similar to the previous downhill slope, in that it has a curve bend at the bottom for a safer transition to the next part of the ride. A curve bend like this was on one of the rides at Dreamworld, the Buzzsaw (Dreamworld.com, 2016). It had a curve bend when the cart came down from the peak of the track to provide a safe transition to the next part.
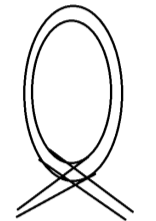 Part E: The Loop
Part E: The Loop
 The loop will be the highlight of the ride to many riders. The radius of the circle is 20m. Now to find the circumference of the loop.
The loop will be the highlight of the ride to many riders. The radius of the circle is 20m. Now to find the circumference of the loop.
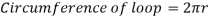
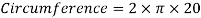
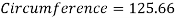
Now to find the KE and the GPE of the cart to see if it has enough energy to make it halfway across the loop. Only the calculations for half of the loop will need to be found as when the cart gets halfway up the loop, gravity will then bring it back down the other half.
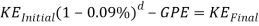
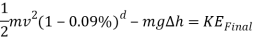
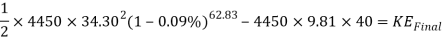
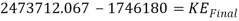
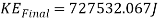
This is the KE at the top of the loop. Now to find the velocity it will be travelling at when it is at the top of the loop.
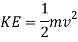
Rearrange to make ‘v’ the subject.
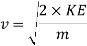
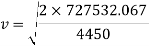
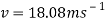
This shows that the cart decelerates from 34 meters per second going into the loop to 18 meters per second at the top of the loop. Now to find the tension acting on the cart, both at the start of the loop and at the top of it.
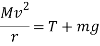
Rearrange to make T the subject.
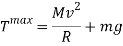
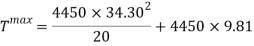
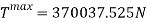
Now to convert this information into acceleration to find the G’s felt on this part.
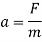
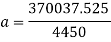
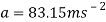
Using this, the G force can now be calculated.
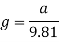
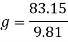
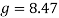
This amount of G’s can kill the riders, therefore the loop must be bigger.
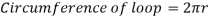
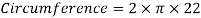
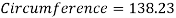
Now to find the KE and the GPE of the cart.
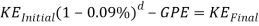
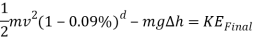
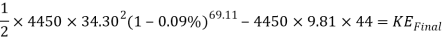
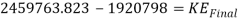
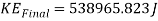
This is the KE at the top of the loop. Now to find the velocity it will be travelling at when it is at the top of the loop.
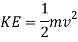
Rearrange to make ‘v’ the subject.
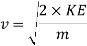

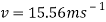
Now to find the tension acting on the cart, both at the start of the loop and at the top of it.
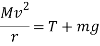
Rearrange to make T the subject.
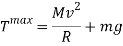
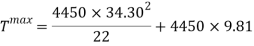
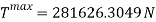
Now to convert this information into acceleration to find the G’s felt on this part.
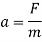
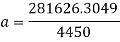
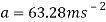
Using this, the G force can now be calculated.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


