Orr-sommerfeld Stability Analysis of Two-fluid Couette Flow
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 1905 words | ✅ Published: 09 Mar 2018 |
ORR-SOMMERFELD STABILITY ANALYSIS OF TWO-FLUID COUETTE FLOW WITH SURFACTANT
- V.P.T.N.C.Srikanth BOJJA1* , Maria FERNANDINO1, Roar SKARTLIEN2
ABSTRACT
In the present work, the surfactant induced instability of a sheared two fluid system is examined. The linear stability analysis of two-fluid couette system with an amphiphilic surfactant is carried out by developing Orr-Sommerfeld type stability equations along with surfactant transport equation and the system of ordinary differential equations are solved by Chebyshev Collocation method[1,2]. Linear stability analysis reveals that the surfactant either induces Marangoni instability or significantly reduces the rate at which small perturbations decay.
Keywords:Linear stability, Orr-Sommerfeld, Marangoni mode, Amphiphilic surfactant.
NOMENCLATURE
A complete list of symbols used, with dimensions, is given.
Greek Symbols
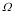 Growth rate
Growth rate
 Surfactant concentration
Surfactant concentration
 Mass density, [kg/m3].
Mass density, [kg/m3].
 Dynamic viscosity, [kg/m.s].
Dynamic viscosity, [kg/m.s].
 Height of perturbed inteface
Height of perturbed inteface
 Surface tension
Surface tension
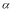 Wave number
Wave number
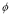 ,
, Stream functions
Stream functions
Latin Symbols
 Capillary number
Capillary number
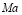 Marangoni number
Marangoni number
 Number of Collocation pints
Number of Collocation pints
 Reynolds number
Reynolds number
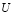 Plate/Wall velocity
Plate/Wall velocity
 Complex wave spped
Complex wave spped
 Width of fluid layer
Width of fluid layer
 Amplitude of Pressure disturbance
Amplitude of Pressure disturbance
 Amplitude of surfactant concentration disturbance
Amplitude of surfactant concentration disturbance
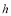 Amplitude of interface perturbation
Amplitude of interface perturbation
 Viscosity ratio
Viscosity ratio
 Depth ratio
Depth ratio
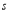 Shear of basic velocity
Shear of basic velocity
 Velocity, [m/s].
Velocity, [m/s].
Sub/superscripts
 Index i.
Index i.
 Index j.
Index j.
 Perturbed quantities
Perturbed quantities
 Base state quantities
Base state quantities
INTRODUCTION
Two layer channel flows and flows with and without surfactants have been given considerable importance because of its numerous industrial applications. Oil recovery[3], lubricated pipelining[4], liquid coating processes[5] are typical industrial situations where Two layer channel flows are often seen. Surfactants also have wide range of industrial applications for example in enhanced oil recovery[6].
Using Perturbation analysis, the primary instability of the two-layer plane Couette–Poiseuille flow was studied by Yih[7] and his studies revealed that even at small Reynolds numbers, the interface is susceptible to long-wave instability associated with viscosity stratification. Yiantsios & Higgins[8] later extended this study for small to large values of wavenumber and confirmed the existence of the shear mode instability. Boomkamp & Miesen[9] came up with the method of an energy budget for studying instabilities in parallel two-layer flows, where energy is supplied from the primary flow to the perturbed flow and instability appears at sufficiently long wave numbers through the increase of kinetic energy of an infinitesimal disturbance with time. In the presence of surfactant at the sheared interface, Frenkel & Halpern[10,11] discovered that even in the stokes flow limit, the interface is unstable as the surfactant induces Marangoni instability, which was later confirmed by Blyth & Pozrikidis[12]. In the case of Stokes flow, they identified two normal modes, the Yih mode due to viscosity stratification inducing a jump in the interfacial shear, and the Marangoni mode associated with the presence of the surfactant. In contrast, at finite Reynolds numbers, infinite number of normal modes are possible and by parameter continuation with respect to the Reynolds number the most dangerous Yih and Marangoni modes can be identified.
In this article, the effect of an insoluble surfactant on the stability of two-layer couette channel flow is studied in detail for low to moderate values of the Reynolds number. To isolate the Marangoni effect, gravity was suppressed in this problem and this was done by considering equal density fluids. Linear stability analysis was carried out by formulating Orr–Sommerfeld boundary value problem, which was solved numerically using Chebyshev collocation method[1][2] for all wavenumbers. Both Marangoni mode and Shear mode are detected and utmost focus is given to Marangoni mode as Shear mode is always stable at moderate to long wavenumbers under the influence of inertia.
The rest of the paper is organized as follows. In § Model description, the governing equations for the system in question are laid out, Normal mode analysis of the physical system is carried out, Orr–Sommerfeld boundary value problem is formulated. General description of Chebyshev collocation method and detailed description of numerical simulation of Orr–Sommerfeld boundary value problem by Chebyshev collocation method and validation of numerical method with literature data is given in § Numerical method. Detailed discussion of results done in § Results. The concluding remarks and outlook for further-work in § Conclusions. Finally acknowledgements in and §Acknowledgemnts.
Model description
Consider two super-imposed immiscible liquid layers between two infinite parallel plates located at , as in Fig. 1. Let the basic flow be driven only by steady motion of plates. It is well known that the basic ‘‘Couette’’ velocity profiles are steady and vary only in the span-wise direction and in the basic state, the unperturbed interface between the liquids is flat and is located at
, as in Fig. 1. Let the basic flow be driven only by steady motion of plates. It is well known that the basic ‘‘Couette’’ velocity profiles are steady and vary only in the span-wise direction and in the basic state, the unperturbed interface between the liquids is flat and is located at . The gravity is suppressed in this problem by considering equal densities in order to investigate the effects of surfactant and inertia on the stability of the system under consideration. The subscripts 1 and 2 refer to the lower or upper fluid, respectively and channel walls move in the horizontal direction, x, with velocities
. The gravity is suppressed in this problem by considering equal densities in order to investigate the effects of surfactant and inertia on the stability of the system under consideration. The subscripts 1 and 2 refer to the lower or upper fluid, respectively and channel walls move in the horizontal direction, x, with velocities  and
and . The interface is occupied by an insoluble surfactant with surface concentration
. The interface is occupied by an insoluble surfactant with surface concentration  which is only convected and diffused over the interface, but not into the bulk of the fluids thus locally changing the surface tension
which is only convected and diffused over the interface, but not into the bulk of the fluids thus locally changing the surface tension  .
.
Governing equations
The mass and momentum conservation equations governing the two-layer system are
 ,
,  (1)
(1)
Where subscript  represents lower and upper liquid layers respectively.
represents lower and upper liquid layers respectively.
Here ,
, 

Figure 1: Schematic sketch of Couette-Poiseuille flow with surfactant laden interface. The perturbed interface  is shown as sinusoidal curve.
is shown as sinusoidal curve.  is the concentration of insoluble surfactant.
is the concentration of insoluble surfactant.
The associated boundary conditions for the system are no slip and no penetration boundary conditions at the walls.
 ,
, at
at  and
and
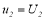 ,
, at
at 
The associated interface conditions are continuity of velocity, tangential stress and normal stress.
Continuity of velocity at the interface
 , at
, at 
The tangential and normal stress conditions at the interface are given by
 (2)
(2)
Where  are stress tensors,
are stress tensors,  is unit normal,
is unit normal, 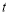 is unit tangent and
is unit tangent and 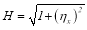
Kinematic interfacial condition is

The surfactant transport equation[13] at the interface is given by
 (3)
(3)
Where  is surface molecular diffusivity of surfactant.
is surface molecular diffusivity of surfactant.  is usually negligible and neglected in this case.
is usually negligible and neglected in this case.
We introduce dimension less variables as follows
 ,
, 
 ,
,  ,
,  ,
,
The dimensionless variables in base state for the couette flow with flat interface  and uniform surfactant concentration
and uniform surfactant concentration 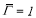 are given by
are given by
 ,
,  (
( ) and
) and
 ,
,  (
( )
)
Where  is shear of basic velocity at interface and is given by
is shear of basic velocity at interface and is given by 
We consider the perturbed state with small deviation from the base state:
 ,
, ,
, ,
, ,
, 
Now we represent disturbance velocity in disturbance stream-functions 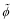 and
and  such that
such that
 ,
, ,
, ,
,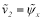
Performing normal mode analysis by substituting
Where  is wave number of the disturbance,
is wave number of the disturbance,  and
and  are constants, and
are constants, and 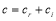 is the complex wave speed. Linearizing the kinematic boundary condition yields
is the complex wave speed. Linearizing the kinematic boundary condition yields
 .
.
Linerarizing the dimensionless x and y-components of Navier-Stokes equation (2) followed by subtraction from the corresponding base state equations and elimination of pressure terms, yields two 4th order Orr-Sommerfield ODEs in stream-functions, one for each fluid.
 (4a)
(4a)
 (4b)
(4b)
Where  is the Reynolds number and
is the Reynolds number and  . (when
. (when ,
, )
)
Boundary conditions at wall in terms of stream-functions are
 (5a)
(5a)
 (5b)
(5b)
Continuity of velocity at interface gives
 ,
,  (5c)
(5c)
Linearization of normal stress condition gives
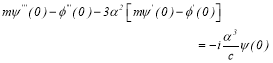 (5d)
(5d)
Linearization of surfactant transport equation gives

Linearization of tangential stress balance condition gives

Where  is the Marangoni number.
is the Marangoni number.
By substituting the value of 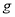 from linearized surfactant transport equation in linearized tangential stress balance condition gives
from linearized surfactant transport equation in linearized tangential stress balance condition gives
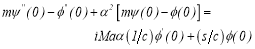 (5e)
(5e)
For each value of  Eqs. (4),(5) forms a eigen value problem, which was numerically solved using chebyshev collocation method[1,2] and QZ algorithm for determining the complex phase velocity
Eqs. (4),(5) forms a eigen value problem, which was numerically solved using chebyshev collocation method[1,2] and QZ algorithm for determining the complex phase velocity 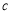 .
.
Numerical method
The two Orr-Sommerfield equations eqs. (4) along with eight boundary conditions eqs. (5) are solved numerically using Pseudo-spectral Chebyshev collocation method[1,2]. To implement the Chebyshev method, we transformed each of the two fluid domains into standard Chebyshev domain 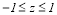 that is
that is
Fluid 1 domain  is mapped to
is mapped to  and Fluid 2 domain
and Fluid 2 domain  is mapped to
is mapped to  by substituting
by substituting  and
and  respectively.
respectively.
Next, we represent each stream function as truncated summation of orthogonal Chebyshev polynomials by setting.
by setting.
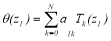 and
and (6)
(6)
Where  and
and  are unknown Chebyshev coefficients and N is the number of Cheyshev collation points in each domain. Upon substituting eq. (6) in eq. (4) and projecting them on to arbitrary orthogonal functions
are unknown Chebyshev coefficients and N is the number of Cheyshev collation points in each domain. Upon substituting eq. (6) in eq. (4) and projecting them on to arbitrary orthogonal functions 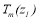 and
and  respectively by taking the Chebyshev inner product,
respectively by taking the Chebyshev inner product,
.
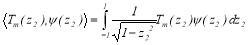
these two Chebyshev inner products forms N-3 equations each summing up to 2N-6 equations and N+1 coefficients in  and N+1 coefficients
and N+1 coefficients 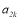 . 2N-6 equations along with 8 boundary conditions obtained by substituting eq. (6) in eq. (5) and 2N+2 coefficients forms a linear system
. 2N-6 equations along with 8 boundary conditions obtained by substituting eq. (6) in eq. (5) and 2N+2 coefficients forms a linear system

Where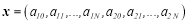 , and
, and ,
, are square matrices of size 2N+2.
are square matrices of size 2N+2.
This generalized eigen value problem was solved by QZ algorithm to obtain  and subsequently growth rate,
and subsequently growth rate, 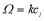 .We used
.We used , above which the eigen values are independent of number of collocation points.
, above which the eigen values are independent of number of collocation points.
The accuracy of the Numerical method is checked by comparing current results with published literature[10] for the Two layer couette flow with an insoluble surfactant in stokes flow limit. To make this comparison, growth rates are calculated by muting the inertial terms by setting in the our code and with same parameters as in Halpern’s[10] Fig 2a and Fig 2b, where growth rates are predicted by long-wave evolution equation. Fig xxx shows excellent agreement between two numerical procedures.
in the our code and with same parameters as in Halpern’s[10] Fig 2a and Fig 2b, where growth rates are predicted by long-wave evolution equation. Fig xxx shows excellent agreement between two numerical procedures.

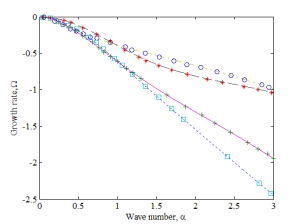
Figure 2: Dispersion curves for the most (a)Unstable

Figure 3: Dispersion curve for the  (solid line),
(solid line),  (dashed line), at
(dashed line), at ,
, ,
, ,
, 
RESULTS and discussions
Blyth and Pozrikidis[14] observed that in the Stoke’s flow limit, there exists two modes that govern the stability of a two-layer couette flow system with surfactant: the Marangoni mode and the Yih mode associated with surfactant and the clean liquid-liquid interface respectively. But on the other hand, in flows with inertia, there exists more than two normal modes. From Fig. 3, the broken line corresponding to  is above the solid line, which corresponds to
is above the solid line, which corresponds to  , it is evident that the surfactant in the presence of inertia has significantly reduced the rate at which small perturbations decay. Earlier stability analysis for stoke flow in presence of surfactant opens up a range of unstable wave numbers extending from zero up to the critical wavenumber
, it is evident that the surfactant in the presence of inertia has significantly reduced the rate at which small perturbations decay. Earlier stability analysis for stoke flow in presence of surfactant opens up a range of unstable wave numbers extending from zero up to the critical wavenumber  .The neutral stability curve Fig. 4 for values (
.The neutral stability curve Fig. 4 for values ( ,
, ,
, 
 and
and  ) is in accordance with the earlier stokes flow stability analysis and in addition at
) is in accordance with the earlier stokes flow stability analysis and in addition at  , a second small window of stable wave numbers appears to form an island of stable modes, with the island tip located at
, a second small window of stable wave numbers appears to form an island of stable modes, with the island tip located at  . In Fig. 5 we plot the growth rate of the Marangoni mode against the Reynolds number, up to and beyond
. In Fig. 5 we plot the growth rate of the Marangoni mode against the Reynolds number, up to and beyond , for
, for  , corresponding to the stable island tip. At
, corresponding to the stable island tip. At , linear stability for Stokes flow predicts the growth rate
, linear stability for Stokes flow predicts the growth rate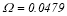 , for the Marangoni mode. The present results confirms that the Marangoni mode at
, for the Marangoni mode. The present results confirms that the Marangoni mode at  marks the inauguration of the lower stable loop.
marks the inauguration of the lower stable loop.
In Fig. 6 for a fixed Reynolds number  , we show the dependence of the growth rates of the Marangoni mode on the wave number. The close-up near
, we show the dependence of the growth rates of the Marangoni mode on the wave number. The close-up near  , presented in Fig. 6(b), shows that the Marangoni mode has negative growth rate for small band of wave numbers ranging from
, presented in Fig. 6(b), shows that the Marangoni mode has negative growth rate for small band of wave numbers ranging from  and has positive growth rate thereafter up-to
and has positive growth rate thereafter up-to 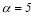 , beyond which the Marangoni mode is stable again. These results clearly demonstrate the crucial role of the surfactant, which either provokes instability or significantly lowers the rate of decay of infinitesimal perturbations.
, beyond which the Marangoni mode is stable again. These results clearly demonstrate the crucial role of the surfactant, which either provokes instability or significantly lowers the rate of decay of infinitesimal perturbations.

Figure 4: Neutral stability curves for  ,
, ,
, 
 and
and 

Figure 5: Growth rate vs. Reynolds number for the Marangoni mode for ,
,  ,
,  ,
,  ,
, 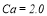 ,
, 
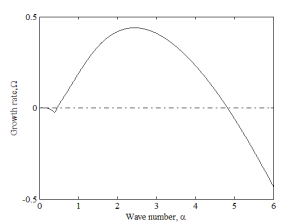

Figure 6: Dispersion curve for the Marangoni mode (solid line) for ,
, ,
, ,
, ,
, ,
, 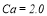 (b) Zoom-in of (a) around
(b) Zoom-in of (a) around 






Figure 7: Neutral stability curves for 
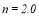 ,
, 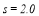 ,
, 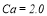 and (a)
and (a)  (b)
(b)  (c)
(c)  (d)
(d)  (e)
(e) 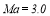 (f)
(f) 
Further, we investigated the effect of Marangoni number on the stability of the system under consideration via Fig 7(a) and this shows that in the devoid of surfactant that is at 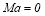 there is very small band of wavenumbers where the system is unstable for any Reynolds number. Moreover around
there is very small band of wavenumbers where the system is unstable for any Reynolds number. Moreover around  the band of unstable wavenumbers is slightly larger than at any arbitrary Re. In presence of surfactant,
the band of unstable wavenumbers is slightly larger than at any arbitrary Re. In presence of surfactant, 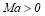 Fig. 7(b)-7(e) a second small window of stable wave numbers appears to form
Fig. 7(b)-7(e) a second small window of stable wave numbers appears to form
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


