Negative Absolute Temperature Thermodynamics

• T.H. Tennahewa

Thermodynamics and Statistical mechanics at Negative Absolute Temperature

We define the temperature, T; by 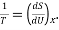in here S stands for Entropy which describes the measure of disorder in the system and U for Internal energy. In here x stands for the partial differentiation that should hold constant in the thermodynamic equation relating TdS and dU. this relation comes from the first law of Thermodynamics. That is;

;

We can define temperature with relating Enthalpy (H) also. That is in here too y stands for the partial differentiation that should hold constant in the thermodynamic equation relating TdS and dH. Below is the derivation of above equation.

We called absolute temperature as a temperature where on the Kelvin scale 0 K as the absolute zero point, where all motion in a classical gas would stop. Most systems, including a classical gas are limited to positive absolute temperatures. In order to be able to reach negative temperatures, a system needs to possess an upper bound for the energy of its particles, which is a maximal possible energy a particle of the system can have. This limit is not an external limit in the sense that there is just no more energy available. It is an internal limit – the particles cannot absorb more energy even if there is plenty available. It is important to note that the negative temperature region, with more of the atoms in the higher allowed energy state, is actually warmer than the positive temperature region. If this system were to be brought into contact with a system containing more atoms in a lower energy state (positive temperatures) heat would flow from the system with the negative temperatures to the system with the positive temperatures.

By the definition of temperature we can describe above figure.

If the energy in the system is minimum (E_min), all particles are in the lowest possible energy state and the entropy is zero. The curve is vertical at this point with an infinite slope and temperature is therefore zero. If the energy increases, the particles begin to occupy higher energy states, and the entropy increases. There are, however, always more particles at low energies than at high energies this is same as the usual Boltzmann distribution. (Figure 2 below) The slope of the entropy versus energy curve decreases and the temperature therefore increases. At some point, when there is enough energy in the system, the particles distribute equally over all energy states. Therefore the disorder and the entropy are maximum. The curve is completely flat at this point, with a slope of zero, and the temperature is therefore infinite. If the total energy in the system is further increased, more particles will occupy high energies than low energies this is same as the inverted of the Boltzmann distribution. Because the energy distribution becomes narrower again, disorder and entropy starts to decrease. This is not a usual behavior because usually entropy increases with increasing energy. The slope of the curve is negative in this region and therefore the absolute temperature is negative. If the energy in the system is maximum (E_max), all particles are at their maximum possible energy. The entropy is again zero. The curve is again vertical therefore the temperature is again zero, but this time it is negative values. Thus, while a temperature of positive and negative infinity is physically identical, temperatures of positive and negative zero are very different. Because of that we could write temperature range as +0 K, +300 K, …, +∞ K, −∞ K, … , −300 K, … , −0 K.

Figure 2- The Maxwell- Boltzmann distribution

In the Carnot cycle of a heat engine heat absorbed from the hot reservoir and heat rejected to the cold reservoir while work done by the system. In that case we define the efficiency of the process as,

In here Q₁ is a heat absorbed at temperature T₁ and Q₂ is a heat rejected at temperature T_2. In heat engine T₂ / T₁ < 1, therefore efficiency is positive. But for negative temperature reservoirs T₂ / T₁ > 1, therefore efficiency is negative and can be very large. In this case work has to be supplied to maintain the cycle.

It should be noted that when Carnot cycle is operated between two negative temperatures that is work is done by the machine while heat absorbed from cold reservoir and rejected to hot reservoir. Efficiency of the system is not only positive but it is also less than unity. Thus at both positive and negative temperatures cyclic heat engines which produce work have efficiencies less than unity that is they absorb more heat than produced work. Second law of thermodynamics should have to modify to use with this kind of Carnot cycle. In there, entropy formulation and Clausius statement remain unchanged and Kelvin-Plank formulation has to be changed. They are mentioned below.

• Entropy formulation

The entropy of a system is a variable of its state and the entropy of an isolated system can never decrease.

• Clausius Statement

It is impossible to construct a device operating in a closed cycle that will produce no other effect than the transfer of heat from a cooler to hotter body.

• Kelvin- Plank formulation

It is impossible to construct an engine, which is operating in a cycle produces no other effect except to external heat from a single reservoir and do equivalent amount of work.

Modified statement:

It is impossible to construct an engine that will operate in a closed cycle and produce no effect other than the extraction of heat from a positive temperature reservoir with the performance of an equivalent amount of work or the rejection of heat into a negative temperature reservoir with the corresponding work being done on the engine.

• Carathéodory form

In any neighborhood of any state there are states that cannot be reached from it by an adiabatic process.

Both first and second laws of thermodynamics can be used at negative temperatures as at positive ones to derive other thermodynamic relations. From these laws it is interpreted that the difficulty of heating a hot system at negative temperatures is analogous to the difficulty in cooling a cold system at positive temperature.

The important requirements for thermodynamical system to be capable for negative temperature are:

• The elements of the thermodynamical system must be in thermodynamical equilibrium among themselves in order to describe the system by temperature.
• There must be an upper limit of the possible energy of the allowed states of the system. It is need a lower bound for the energy in order to get positive temperatures and an upper bound in order to get negative temperatures.
• The system must be thermally isolated from all systems which do not satisfy both of the above conditions.

To satisfy the second condition negative temperatures are to be achieved with a finite energy. In thermal equilibrium the number of elements in the m^th state is proportional to the Boltzmann factor; here W_m is energy of the m^th state.

Boltzmann distribution function which is formed using Boltzmann factor is given below.

In negative temperature case when W_m increases with that Boltzmann factor increases exponentially therefore high energy states are more occupied than low energy states. As a result of this we could say that without an upper limit to the energy negative temperatures could not be achieved with a finite energy. Since most of the systems do not satisfy this conditions negative temperatures are occurs rarely.

Spin systems sometimes form the thermodynamic systems which can describe by using temperature. In there for a system of electron spins in a lattice, a temperature such that the population of the energy levels of the spin system is given by the Boltzmann distributionwith the spin temperature. To achieve thermodynamic equilibrium various nuclear spins must interact among themselves. This happened due to nuclear spin-spin magnetic interaction.

Subatomic particles like electrons, protons and neutrons can be imagined as spinning on their axes. In many atoms these spins are paired against each other, such that the nucleus of the atom has no overall spin. In some atoms the nucleus has shown overall spin. The rules for determining the net spin of a nucleus are given below;

• If the number of neutrons and the number of protons are both even, then the nucleus has NO spin. (Classical Particles)
• If the number of neutrons plus the number of protons is odd, then the nucleus has a half-integer spin (i.e. 1/2, 3/2, 5/2) (Fermions)
• If the number of neutrons and the number of protons are both odd, then the nucleus has an integer spin (i.e. 1, 2, 3) (Boson)

It is defined in Quantum mechanics that a nucleus of spinIwill have 2I+ 1 possible orientations. A nucleus with spin 1/2 will have 2 possible orientations. In the absence of an external magnetic field, these orientations are of equal energy. If a magnetic field is applied, then the energy levels split. When the nucleus is in a magnetic field, the initial populations of the energy levels are determined by thermodynamics, as described by the Boltzmann distribution. It means that”the lower energy level will contain slightly more nuclei than the higher level”. It is possible to excite these nuclei into the higher level with electromagnetic radiation. The frequency of radiation needed is determined by the difference in energy between the energy levels.

This spin-spin process can be characterized by using relaxation process. Nuclei in the higher energy state return to the lower state by emitting the radiation. At radio frequencies, re-emission is negligible. There are two main relaxation processes;

• Spin – lattice (longitudinal) relaxation
• Spin – spin (transverse) relaxation

Spin – lattice relaxation (T₁)

Nuclei which are in a sample create a complex magnetic field. The magnetic field caused by motion of nuclei within the lattice is called thelattice field. This lattice field has many components. Some of these components will be equal in frequency and phase to the Larmor frequency of the nuclei of interest. These components of the lattice field can interact with nuclei in the higher energy state and cause them to lose energy returning to the lower state. The energy that a nucleus loses increases the amount of vibration and rotation within the lattice resulting in a tiny rise in the temperature of the sample.

The relaxation time,T₁(the average lifetime of nuclei in the higher energy state) is dependent on the magnetogyric ratio of the nucleus and the mobility of the lattice. As mobility increases, the vibrational and rotational frequencies increase, making it more likely for a component of the lattice field to be able to interact with excited nuclei. However, at extremely high mobilities, the probability of a component of the lattice field being able to interact with excited nuclei decreases.

Spin – spin relaxation (T₂)

This is describing the interaction between neighbouring nuclei with identical precessional frequencies but differing magnetic quantum states. In this case, the nuclei can exchange quantum states; a nucleus in the lower energy level will be excited, while the excited nucleus relaxes to the lower energy state. There is nonetchange in the populations of the energy states, but the average lifetime of a nucleus in the excited state will decrease. This can result in line-broadening.

Most of the nuclear systems don’t satisfy the conditions in negative temperatures.

By looking at all these things we can conclude that although the phenomena of negative temperature is a fully valid concept in thermodynamics and statistical mechanics they have less important than phenomena of positive temperature.

1