Monte Carlo Simulation of Transmission Experiement

Fluid Densitometer Design based on Transmission and Scattering Gamma Ray Method using Monte Carlo Approach

R.Wirawan, M. Djamal, A.Waris, G. Handayani, H.J. Kim

Abstract. Non-destructive testing is one method in the material testing that was applied and developed for many purposes in the industrial field. Gamma spectrometer is a one method that can be applied for the fluid densitometer. It was studied the potential of the use of transmission and scattering gamma ray measurements in order to evaluate the fluid density using GEANT4 Monte Carlo simulation toolkit.

Keywords: Non-destructive testing, scattering gamma, Monte Carlo, GEANT4.

PACS: 29.40.-n

Introduction

Gamma-ray spectrum measurement is one of promising developing method in the non-destructive test application especially for an online measurement. It’s applicable for many industrial applications such as in medical, mining and oil industry, homeland security.

The quality of the material can be differentiating from another one based on its density. In the application of gamma spectrometry, it’s influence the gamma ray energies spectrum detection result. Ball et al. (1998) have investigated the response of gamma backscatter to the spatial density in bulk sample [1]. In the fluid product analysis especially for the oil product density measurement, it’s a promising method for a densitometer. Hussein (2011) has developed investigation of the fluid flow in the pipe using gamma spectrometry [2]. Khorsandi and Feghhi have analyzed the transmission mode in densitometer application for the petroleum products monitoring applications [3].

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

The combination of transmission and scattering measurement modes are good approaching for a better analysis method in the detector response measurement due to the fluid density inside the pipe. For this purpose, simulation using Monte Carlo method can be conducted. Monte Carlo methods have capabilities in the implementation of the several of physics models and give the predicting result in the radiation physics application [4, 5]. In the present study we investigated the potential of the combination of these measurements using the Monte Carlo radiation transport from GEANT4 simulation toolkit.

Theory

Gamma ray energy spectrum characteristic that detected from its interaction with the material have information to identify the material characteristics involved. In the gamma ray spectrum measurement, there are two kinds of measurement type i.e. transmission and scattering. In the transmission, the gamma ray beams have an attenuated intensity because of energy absorption by material. The mass attenuation coefficient  of photon is a function of photon energy. The attenuated intensity was described by the Beer–Lambert formula:

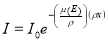(1)

where I₀ incident gamma rays intensities, x is material absorption thickness, is mass absorption coeficient and its proportional to the total cross-section as follows , N_A is the Avogadro’s number (6.02×10²³ atom/mole) and A is atomic mass number of material[8].

For the scattering measurement, the detected photon beam is the result of deflecting with an electrons material. Scattering interactions that may occur is the single scattering or multiple scattering.The photon beam intensity has attenuation in the path before the scattering point interaction and in the path to the detector after the scattering point interaction. Figure 1 shows the single scattering interaction of photon with an element volume dV.

Figure 1 Schematic diagram of photon single scattering interaction with an element volume in the material (adopted from Devlin and Taylor) [9].

According to the Compton scattering interaction, the photon with an energy E_ will be deflected with scattering angles  to the origin direction after collision with an atomic electron. The scattered photon energy (E_Scatt) is expressed by the formula:

(2)

The intensity of detected gamma photon are influence of attenuation along primary photon, number of electron in element volume, differential cross-section, attenuation of scattered photon path and the solid angle subtended by detector at the element volume. For the single scattering interaction, the intensity of detected photon as depicted in the formula:

(3)

where S is the source activity (photon s^-1), dV is element volume interaction, n is the electron density of the material, r₁ and r₂ are the length path of the primary photon before interaction and after scattering respectively. The density  of the material is related to the electron density by (4)

where N_A is the Avogadro number, Z is the atomic number and M is the atomic mass.

For the Compton interaction probabilities of the photon beam when it interact with an electron of the material was describe in differential form by Klein-Nishina formula,

(5)

where r₀ is clasical electron radius (2,82 fm) and P parameter as function of incident photon energy and scattering angles  as the formula

(6)

where constant [1,8]. Using the equation (4) and (5) to substitute parameter n and in the equation (3), we have the relation of intensity with the material density:

(7)

Solution of the equation (7) can be expressed in the simple form:

(8)

where A and B are constant.

Method

The simulation setup was developed based on the transmission configuration which conducted experimentally done by Khorsandi [3]. Four detectors are placed in two type positions where two detectors in the same side with source and two others in the opposite site as shown in Figure 2. The spatial distance between two detector d10 and d30 from the collimated source axis are about axis 27.5cm. For detector d20 is placed 20 cm far away from detector d10. Polyethylene pipe have an inner radius 5cm and thickness it’s about 2mm. Fluids under investigation inside the pipe (i.e. gasoline, gasoil and water) are assumed to be of uniform density. A disk gamma ray source model is used for Cs-137 source is collimated by the cylinder shielding lead with 5cm thickness. The 3in. x 3in. NaI(Tl) detector model reconstruction in the simulation is adopted from references [6, 7]. Simulation based on GEANT4 Penelope Monte Carlo using 5.0 x 10⁷ of the gamma source beamon.

Figure 2 Schematic visualization of GEANT4 simulation for the transmission and scattering measurements setup.

Result and Discussion

To examine the response function of transmission and scattering measurement, firstly we need to consider the setup designed for the detector construction according to the c gamma source energy spectrum. The Cesium 137 source was placed in front of the Pb collimated NaI(Tl) 3 in. x 3 in. scintillation detector. Figure 3 shows the detector response function spectrum of GEANT4 simulation result comparing to the measurement result of the 15uCi gamma source. There are a good agreement for photopeak energy between the simulation result and the experiment result.

Figure 3 Response function of Cs137 15uCi gamma source for 3 in. x 3 in NaI(Tl) detector.

Based on detector construction setup, then we analyzes the detector response function of transmission and scattering measurement. Figure 4 shows the response function result of detector that placed in the four different positions for three different type of density fluid i.e. gasoline, gasoil and water.

Figure 4 Response function of detector NaI(Tl) 3in. x 3in. from GEANT4 simulation of four different detector positions for gasoline, gasoil and water fluids in pipe.

In the all energy spectrum distribution above, density of fluid matter give an effect to the gamma energies spectrum. The gasoline has a lower density number, but it shows a higher intensity (number of events) of gamma ray energy detected compare to the gasoil and water. The increased density of fluid will increased the number of electrons at the scattering point interaction, attenuation of primary and scattered photons. So, it’s give an effect to the decreasing intensity or peak energy spectrum that detected by the detector.

For transmission mode as shown at d0 detector position, the main peak of Cesium 137 gamma source is in the 0.662 MeV. The normalize peak intensity shows that the GEANT4 simulations result have a good agreement to the Khorsandi (2011) experiment result as shown in Figure 5. This result shows that the model can be used for predicting the fluid densitometer experiment.

Figure 5 Normalize intensity curve of transmission mode (d0 detector position) from simulation and experiment results.

Here in the Figure 6(a), we have the same trends that the decreasing of the photopeak height due to the fluids density increase.

Figure 6 Gaussian height curves of photopeak at four different detector positions.

Based on the intensity as density function equation (8), the proposed constant A and B for the curve fit in the Figure 6(a) are depicted in Table 1.

Table 1. Curve fitting constant

Based on the B constant of the four normalize count rates curves, d20 detector position have a higher decreasing slope than the others. In other side, the number of entry photon to the detector d20 position is too small, so for this configuration its need the higher activity source.

Conclusions

In this study, a Monte Carlo simulation of transmission and scattering measurements of gamma ray for the fluid densitometer was carried out using GEANT4. Due to an increase in the fluid density in the pipe, the peak heights of detected gamma ray intensity have decreased. The simulations for the gamma ray transmission investigation were conducted according to the experiment setup give the best fit curve result.

Acknowledgments

The author acknowledges the financial support of Directorate General of Indonesian Higher Education through the Sandwich-Like (PKPI) Program 2013.

Refference

[1] A.J. Ball, C.J. Solomon, J.C. Zarnecki, The response of gamma backscatter density gauges to spatial inhomogeneity – An extension of the single scattering model, Nuclear Instruments and Methods in Physics Research B 140 (1998) 449-462.

[2] Nagy M. Hussein, Investigation of Fluid Flow using Gamma Spectroscopy, World Academy of Science, Engineering and Technology 80 2011 1169-1174.

[3] M. Khorsandi, S.A.H. Feghhi, Design and reconstruction of a prototype gamma-ray densitometer for petroleum products monitoring applications, Measurement 44 (2011) 1512-1515.

[4] U.A. Tarim, E.N. Ozmutlu, O. Gurler, S. Yalcin, The Effect of the Housing Material on NaI(Tl) detector response function, J. Radioanalytical and Nucl. Chem. DOI 10.1007/s10967-012-1716-z (2012) 1-5.

[5] A.F. Bielajew, Fundamentals of the Monte Carlo method for neutral and charged particle transport, Department of Nuclear Engineering and Radiological Sciences, The University of Michigan, 2001, pp.1-10.

[6] Hu-Xia Shi, Bo-Xian Chen, Ti-Zhu Li, Di Yun: Precise Monte Carlo simulation of gamma-ray response functions for an NaI(Tl) detector, Applied Radiation and Isotopes 57 (2002) 517–524.

[7] Abd-Elzaher, M., Badawi, M. S, El-Khatib, A. and Thabet, A. A.: Determination of Full Energy Peak Efficiency of NaI(Tl) Detector Depending on Efficiency Transfer Principle for Conversion From Experimental Values, World Journal of Nuclear Science and Technology, (2012), pp. 65-72.

[8] Knoll, G.F., Radiation Detection and Measurement (Second Edition), Wiley and Sons, New York, 1989.

[9] G. Devlin, D. Taylor: The Spatial Response Pattern of Gamma Backscatter Density Gauges, Journal of Soil Sciences Vol. 21 No. 2 (1970), pp. 297-303.