Generation of Extreme Ultraviolet Radiation
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 3147 words | ✅ Published: 11 Sep 2017 |
Generation of Extreme Ultraviolet Radiation from Intense Laser-Plasma Interactions using Two-Colour Harmonics
BRIEF HISTORY
Over the past few decades breakthroughs in the production of intense laser fields have meant that multi-terawatt and even petawatt systems are now standard in laboratories**. This has been achieved through reduction of the pulse duration, originally from nanosecond pulses down to femtosecond and recently reaching attosecond levels (1as =10-18s)**. This coupled with important improvements to systems, such as the chirped pulse amplification technique (CPA)**, has allowed laser pulses to be amplified to higher peak powers than ever before and used in laser-matter interactions. The resulting scientific drive from developments such as these pushed achievable laser intensities from 109W/cm2 to the 1014W/cm2, at which the interaction between these high intensity lasers and dense electron-free gas was studied**.
Only recently thanks to advances in both laser performance and computer simulation tools has study on laser-plasma interactions in the generation of HHG made progress, providing the possibility to generate sources of incoherent electromagnetic radiation of short wavelength and pulse durations**. As further study was carried out on the interaction of light with relativistic free electrons in plasma, it has reached a point now in which generation of high-harmonics of the fundamental laser, soft and hard x-rays, and shorter pulse duration (1as) lasers of intensities reaching 1018W/cm2 are now possible**. Due to this the generation of high-order-harmonics from high-intensity laser interactions has been a major area of attoscience research within the last decade.
HHG PRODUCTION
High harmonic generation (HHG) refers to the process in which a high intensity laser pulse is focused onto a target, classically a noble gas, in which strong nonlinear interactions result in the generation of very high harmonics of the optical frequency of the pulse**. This will occur for intensities of 1014W/cm2 and above, where typically only a small amount of this energy is converted into the higher harmonics. From these high-harmonics, spatially and temporally coherent attosecond pulses of extreme ultraviolet light can be generated, which can then be used as a reliable source of highly tuneable short wavelength radiation in many different applications e.g. x-ray spectroscopy**.
In the case of high intensity laser-gas interactions this is achieved by tailoring the intensity of the laser pulse so that its electric field amplitude is similar to the electric field in the target atoms**. From this the laser’s electric field is able to remove electrons from the atoms through tunnel ionisation, at which point the electrons are accelerated in the field and, with certain conditions controlled, are made to collide with the newly created ion upon recombination. The resulting collision generates the emission of high energy photons**, as shown in fig 1.
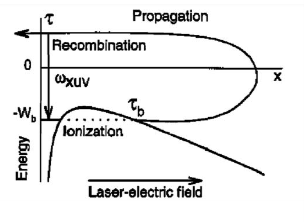 Fig. 1: HHG three step model.
Fig. 1: HHG three step model.
This is known as the three step model; electron is detached from atom through tunnel ionisation, then accelerated within the field away from atom, then accelerated back towards atom where it collides and recombines, from this collision all the energy lost appears as emitted HHG ultraviolet photons.
HHG from laser-gas interactions have been used extensively to generate attosecond pulses but is limited in flux and photon energy by low conversion efficiencies between the driving laser energy and the attosecond pulses, this can be attributed to two key factors; loss of phase matching between the driving laser to the generated extreme ultraviolet (XUV) radiation as its propagated through the gas over a relatively large distance, and a restriction on the intensity of the driving laser due to the ionisation threshold of the target gas, this saturation intensity is roughly 1016W/cm2**. Meaning laser intensities above this threshold limit will over-ionise the gas leaving no neutral atoms left to generate the XUV harmonics.
The use of laser-solid interaction offers the opportunity of reaching much higher attosecond pulse intensities and generation efficiencies beyond the capabilities of gas based HHG**. The method of generating high-harmonics in laser-solid interactions is fundamentally different than that of laser-gas interactions.
Interaction of intense ultrashort laser pulses (of pulse duration around a few femtoseconds) on an optically polished solid surface results in the target surface being completely ionised, generating a dense plasma which will act as a mirror, called a plasma mirror**. The reflection of these high intensity laser pulses will be affected by a wave motion set-up in the electrons within the plasma surface causing it to distort the reflected laser field, resulting in the production of upshifted light pulses and the generation of high-order harmonics**. Due to the coherent nature of this process, these generated harmonics are phase-locked and emerge as attosecond pulse.
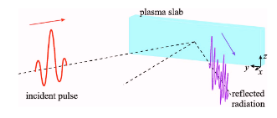
Fig. 2 Laser pulse moving towards overdense plasma.
A key property of this plasma is its electron density, this determines whether the laser is reflected, absorbed or not allowed to pass through. This is known as the density gradient scale length, as the laser pulse interacts with the target and forms a plasma it creates a profile that extends out into the vacuum, forming a plasma density profile. This is a critical factor in HHG and consists of two regions:
Overdense scale length, Lod –
If the electron density is equal to the critical density of the target or above, extending up to the maximum target density, the laser pulse is unable to penetrate through the target and is so reflected or absorbed.
Underdense scale length, Lud –
If the electron density is below this critical density the laser will penetrate through, with some absorption.
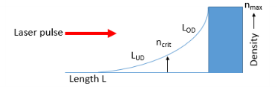
Fig. 3 Plasma density profile, Lud is underdense region, Lod is overdense region.
The critical density is determined from:
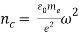
Where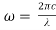 is the angular frequency of the laser.
is the angular frequency of the laser.
As stated before the target surface is highly ionised by the leading edge of the laser pulse, known as the pre-pulse, therefore becoming rapidly over-dense and creating a plasma mirror of sufficient electron density, ne>nc**. HHG within plasma requires laser intensities >1015W/cm2 for 800nm field**, which is usually stated in terms of a normalised vector potential of a0, where:
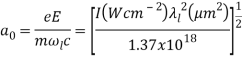
In which; e and m are electron charge and electron mass respectively. c is speed of light in vacuum. E is the amplitude of the lasers electric field. I is the lasers intensity. ωl is the laser frequency and λl is the laser wavelength.
Therefore HHG in plasma requires at least an a0≥0.03.
Recently is was discovered** that there are two mechanisms that lead to HHG from solid density plasma surfaces;
– Relativistic oscillating mirror (ROM)
– Coherent wake emission (CWE)
These two process result in different distortions to the reflected laser field and therefore a completely different harmonic spectra produced.
CWE
Coherent wake emission is a process of three steps;
- Electrons on the surface of the plasma are drawn into the vacuum by the laser field and accelerated back into the dense plasma once they have gained energy from the driving laser field.
- When propagating within the dense plasma these fast electrons form ultrashort bunches, creating plasma oscillations in their wake.
- Within the non-uniform region of the plasma (produced from the density gradient between the plasma-vacuum boundary) the electron oscillations will radiate energy in the form of light of various local plasma frequencies found within this gradient.
This process will occur once for every laser cycle therefore the spectrum of the emitted light will consist of harmonics of the laser frequency, in which CWE harmonic spectra have a cutoff at the maximum plasma frequency ωpmax **. This mechanism is predominant at moderately relativistic intensities of a0≤1, and short but finite plasma gradient lengths of  **.
**.
Coherent wake emission has only recently been identified as a factor in HHG in laser-solid interactions but it is known that it along with ROM contributes to the generation of high-harmonic orders below ωpmax and the strength of their respective influence below this threshold is determined by laser intensity**.
ROM
The other mechanism involved in the generation of high-harmonics from laser-plasma interactions is the relativistic oscillating mirror process, this dominates for relativistic normalised vector potentials of a0>>1, although recent studies have shown that ROM harmonics can be observed even at lower intensities when the plasma gradient length is about  **.
**.
ROM process occurs when surface electrons in the plasma are oscillated collectively by the high intensity incident laser field to relativistic speeds, the plasma will reflect what it observes as a laser pulse of frequency ω+. This ω+ frequency is a higher upshifted frequency of the fundamental pulse due to a Doppler effect produced from the relative motion of the laser field to the moving reflection point on the oscillating plasma surface. The actual reflected laser pulse will have a frequency of ω++ due to a second Doppler upshift effect as it moves towards an observer/target. This is known as Einstein’s relativistic Doppler effect, in which the reflected pulse frequency is upshifted by a factor of 4γ2**. 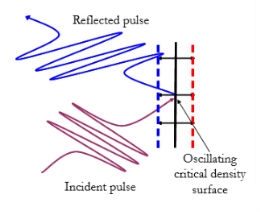
Fig 4. Schematic of a relativistic oscillating critical density plasma interaction.
From past research it has been found that from this mechanism a power-law decay scaling of I(n)ROM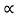 n-8/3 is dominant (where n is the harmonic order) in the harmonic spectrum for harmonic orders above the CWE cut-off point, nCWE,** this is the harmonic order related to the maximum plasma frequency of the target, ωpmax, mentioned previously. Where:
n-8/3 is dominant (where n is the harmonic order) in the harmonic spectrum for harmonic orders above the CWE cut-off point, nCWE,** this is the harmonic order related to the maximum plasma frequency of the target, ωpmax, mentioned previously. Where:
nCWE = nωmax = ωpmax/ωl = 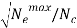
In which; ωl is the frequency of the laser, 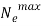 is the maximum electron density of the target, Nc is the critical density shown previously.
is the maximum electron density of the target, Nc is the critical density shown previously.
From this process initial femtosecond pulses can be used to create attosecond pulses. When coupled to a relativistic oscillating mirror it adds an oscillatory extension to Einstein’s relativistic Doppler effect, so due to the periodic motion of the mirror to the laser field and the double Doppler upshifts this results in the production of extreme ultraviolet (XUV) harmonics**. These ultra-short pulses have been the focus of much scientific research recently as they offer a promising way to resolve in the time domain the ultrafast dynamics of electrons within materials**.
Although the relativistic oscillating mirror process is more suited as a macroscopic model for the effective reflection point of the laser field. It assumes that the surface electrons bunch together as the target is ionised and move out into the vacuum to form the plasma where they remain in the overdense region ensuring that the laser field is completely reflected. More recently studies have discovered there is another mechanism in the relativistic regime that can contribute to the harmonic spectrum via a different process entirely.
CSE
This other process is known as Coherent synchrotron emission (CSE)** and is needed to explain observations that do not fit the previous two models, in which dense electron nanobunches are created at the plasma-vacuum boundary where they produce coherent XUV radiation through coherent synchrotron emission. This is a microscopic model of HHG in laser-solid interactions. It models the electrons in the plasma moving, in dense bunches, under the influence of the incident laser field and subsequent fields produced from the movement of charges within the plasma. These nanobunches are periodically formed and coherently accelerated through an instantaneously synchrotron-like orbit during each laser cycle, for oblique laser incidences. As certain conditions, such as ultrashort plasma density scale length, are met these bunches emit bursts of sub-femtosecond intense high-frequency radiation. This radiation has properties dependent on the electron trajectories and it has been shown that it can be modelled as synchrotron radiation**, therefore the coherent XUV emissions are distinctly different from that produced in ROM from relativistic Doppler upshifts. In reality actual electron dynamics may be a mix of CSE and ROM, but due to the complex nature of the changing fields within a plasma it makes it impossible to analytically model with accuracy. Therefore requiring the use of computer simulations to deal with the electron trajectories and their respective radiation emissions.
PREVIOUS EXPERIMENTS
Based on the work of Edwards et al, 2014, in which the study of attosecond XUV pulse generation from relativistic driven overdense plasma targets with two-colour incident light was performed they used 1D, three velocity, particle-in-cell (PIC) code simulations, which treat oblique incidence with boosted frames, to show how pulse intensity can be improved. They converted a small amount (~5%) of the fundamental laser field energy to an additional laser operating at the second harmonic of the fundamental frequency, to significantly enhance the intensity of the generated attosecond pulses by multiple orders of magnitude.
This was based on previous work in which mixing of the fundamental driving laser frequency with the second harmonic was performed on laser-gas interactions to increase the attosecond pulse intensity and isolation (K. J. Schafer et al, 1992).
Edwards demonstrated that a significant improvement was also possible through this mixing method in laser-solid interactions following the Similarity theory (proposed by Gordienko and Pukhov,**), that suggests the behaviour of laser-plasma interactions follow a similarity parameter of:
1/S = a0/N 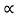 ωl
ωl
Where S = ne/a0nc, is a similarity parameter and N = ne/nc which is the ratio of electron density of the plasma to its critical density.
Therefore from this it would appear that by doubling ωl while using the same laser field amplitude the reflected attosecond pulse intensity would also be increase by a factor of two.
One of the main limiting parameters in these experiments is the achievable value of a0, while the largest solid material value of N (lithium at λ=800nm) is 75, so this type of frequency doubling appears to be a promising pathway to optimising attosecond pulse intensity, although a drawback of this is the negative effect it has on the isolation of the reflected pulses.
Therefore they stated that a two-colour method, of partially converting a portion of the fundamental laser field energy to the second harmonic, would be a more attractive alternative. Through this process the advantages of using a higher incident frequency, by increasing the gradient of the electric field at certain points within the pulse generation cycle, without the related decrease in pulse isolation and loss of energy associated to simple frequency doubling can be exploited.
In their study they used a normal-incidence beam on a step-like plasma density profile using a mix of the first and second harmonic with a phase difference of 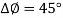 to produce harmonics with a higher intensity than either incident field individually. They demonstrate substantial gains after the addition of a small amount of the second harmonic to achieve attosecond pulse enhancement of factors >10. As well as a 10-fold enhancement when using density gradients of 0.05λ and 0.15λ with conversions of the fundamental to the second harmonic of 5%-10% at an angle of incidence of ϴ=30o.
to produce harmonics with a higher intensity than either incident field individually. They demonstrate substantial gains after the addition of a small amount of the second harmonic to achieve attosecond pulse enhancement of factors >10. As well as a 10-fold enhancement when using density gradients of 0.05λ and 0.15λ with conversions of the fundamental to the second harmonic of 5%-10% at an angle of incidence of ϴ=30o.
Therefore Edwards was able to go on and state that the relative phase of the two incident harmonics were a critical factor in the improvement in attosecond pulse intensity. This is due to the difference in the driving electric field waveform and corresponding resultant electron motion as 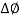 is varied. Where they linked the strongest attosecond pulse intensities with sharp transitions in the driving electric field that are aided by the addition of the second harmonic at optimum phases, while phases that break the driving field transition reduce the attosecond intensities to levels sometimes substantially below what could be achieved pre-mixing of the harmonics.
is varied. Where they linked the strongest attosecond pulse intensities with sharp transitions in the driving electric field that are aided by the addition of the second harmonic at optimum phases, while phases that break the driving field transition reduce the attosecond intensities to levels sometimes substantially below what could be achieved pre-mixing of the harmonics.
Therefore when harmonics are combined without thought to their phases they do not always improve the attosecond strength.
Further detail into the trajectories of dense electron bunches, which emit synchrotron like radiation (CSE) was given to help explain this effect, where supressed pulse electrons were shown to follow a longer and slower motion before being accelerated and subsequently emitting, resulting in longer elongated trajectories. Whereas electrons that contribute to the improvement of the attosecond pulse strength are shown to experience a larger field before and during emission. This meant their velocity and acceleration components were larger than the suppressed electrons, giving them more energy as it is driven back into the plasma.
Overall they state that the larger the electric field experienced by the electrons increases the intensity of the reflected attosecond pulse, due to the number of electrons travelling in a dense bunch increasing as this larger field that the electrons near the surface experience compresses them into higher density bunches.
Another study performed by Yeung et al, 2016, focused on controlling the attosecond motion of strongly driven electrons at the boundary between the pre-formed plasma and the vacuum. They demonstrated experimentally that by precisely adding an additional laser field, at the second harmonic of the fundamental driving frequency, attosecond control over the trajectories of the dense electron bunches involved in intense laser-plasma interactions can be achieved. From this considerable improvements in the high-harmonic generation intensity was observed, which confirms the theoretical work by Edwards in two-colour fields reviewed previously while developing upon this to further factors.
Experimentally they showed that attosecond control over the phase relationship of the two driving fields is necessary to optimise the reflected attosecond pulse intensity. While also using PIC simulations to determine the optimal and worst phase relationships, in which a phase of 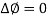 was found to optimise the emission.
was found to optimise the emission.
Microscopic focus determined that during each cycle the emission of the attosecond pulse begins as a primary electron bunch which is compressed and then quickly accelerated away from the surface up to relativistic velocities, from here it emits before it disperses and returns back to the plasma. Secondary bunches are also present but these were found not to have a significant effect harmonic spectrum for orders >20. These bunches were found to emit when their velocities where at their max, which confirmed that the two-colour field phase matched the emitted XUV to the acceleration produced from the fundamental laser field. While at the poorest phase relationship, which Yeung found to be 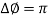 , a plateau in the driving laser field is created which impedes the acceleration of the electrons from the surface, therefore reducing the density of the electron bunch produced that can emit.
, a plateau in the driving laser field is created which impedes the acceleration of the electrons from the surface, therefore reducing the density of the electron bunch produced that can emit.
They concluded from the data provided by the simulations that control of the relative phase of the two colour driving fields has a significant effect the electron bunch dynamics.
While from the experimental data their collected it was demonstrated that the HHG produced from the two-colour field was increased substantially when no laser pre-pulse was involved, or equivalently when the plasma has shorter density scale length. Confirming the work of Edwards et al, 2014, that two-colour fields generate significantly more higher-harmonic orders than that of a fundamental field alone, even when only a small percentage (5%-10%) of the fundamental laser energy is converted to the second harmonic.
INTRODUCTION TO TWO-COLOUR HARMONICS
———————-
ABSTRACT
- BRIEF SUMMARY OF EXPERIMENT, RESULTS AND CONCLUSION 1x
INTRODUCTION
- BRIEF HISTORY .5x
- HHG PRODUCTION .5x
- CWE 1x
- ROM 2x (inc. plasma theory e.g. scale length)
- CSE 1x
- COMPARISON WITH GAS EXPERIMENTS 1x
- PAST EXPERIMENTS LEADING UP TO THIS ONE 2x
- INTRODUCTION INTO SPECIFICS OF THIS EXPERIMENT 1x
METHOD
- PIC CODES EXPLAINED 2x
- EPOCH DETAILS 1x
- LASER DETAILS 1x
- PROCESS OF ANALYSIS .5x
- CREATION OF GRAPHS .5x
RESULTS
- GRAPHS
- COMPARE & CONTRAST
- IMPLICATIONS
CONCLUSION
- FURUTRE RESEARCH 1x
- IMPROVEMENTS 1x
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


