First-principles Calculations of Rare Earth Diffusivities

First-principles calculations of rare earth (Y, La and Ce) diffusivities in bcc Fe

ABSTRACT: The impurity diffusivities of rare earth elements, Y, La and Ce, in bcc Fe have been investigated by the first-principles calculations within nine-frequency model and semi-empirical corrections for magnetization. The microscopic parameters in the pre-factor and activation energy have been calculated. For the three elements, the solute-vacancy interactions are all attractive, and Y and La solute atoms more favorably bond to the vacancy. The solute-vacancy binding energy can be explained in terms of the combination of the distortion binding energy and the electronic binding energy, and the strain-relief effects accounts for larger portion of the binding energy for Y and La than that for Ce. The diffusion coefficients for Y and La are comparable, and predicted to be larger than that for Fe self-diffusion. Compared with Y and La, Ce shows large migration energy and weak solute-vacancy attractive interaction, which accounts for the lowest diffusivity of this element.

Keywords: Diffusion; Rare earth; Bcc Fe; First-principles calculations

1. Introduction

In the past years, the addition of rare earth (RE) elements has been regarded promising in steels [1-3]. A series of beneficial research for the development of Rare earth Addition have been focused on the purification and modification of inclusion, since RE elements are characterized by significant negative free energy changes for compound formations. RE doping also improve the high-temperature oxidation resistance of steels due to the reactive-element effect (REE) [4,5].In addition, the phase transformations, recrystallization behavior, and the corrosion resistance of steel can be improved by adding RE [6, 7].

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

Knowledge of all of these is essential to understand the influence of RE additions on the physical, chemical and various properties of steels. In spite of the progress so far in RE application, it is apparent that many questions still remain rather controversial. Data for the effects of rare earths on the surface and interfacial properties, surface tension, contact angle, etc., of steels, are unanswered, for the sake of precise solubilities of rare earths in iron and steels are still not available. Furthermore, accurate thermodynamic data are still unsatisfactory, to accurately predict these characteristics. Kinetic properties, in particular diffusion coefficients for RE, are necessary in understanding the underlying mechanism of RE’s above effects [8]. Therefore, the investigation of the diffusivity for these RE elements is expected to be useful in the context of developing RE steels.

Although for diffusion in bcc Fe many data are available, nevertheless there is little experimental or calculated data for RE. For the three commonly used RE elements, Y, La and Ce, only the diffusion coefficient of Y has been reported [9].The purpose of the present work is to investigate the impurity diffusivities of rare earth elements, Y, La and Ce, in bcc Fe by the first-principles calculations within nine-frequency model and semi-empirical corrections for magnetization[10,11], calculate the associated solute-vacancy binding energies, migration energies, pre-factors and activation energies for these impurity diffusivities, as well as the self-diffusion coefficient of Fe, thus discuss the related factors of the diffusion coefficients.

2. Methodology

The temperature dependence of diffusion coefficient D is expressed in the Arrhenius form D=D₀exp(-Q/k_BT). For bcc Fe, the Arrhenius plot of self-diffusion and solute diffusion in iron of the ferromagnetic state deviates downwards from the Arrhenius relationship extrapolated from the paramagnetic state [12]. This effect is attributed to the change of magnetization which affects the diffusion activation energy. The temperature dependent magnetization on the diffusion activation energy is well described by the following form [13]:

QF(T)=QP[1+αs(T)2] (1)

where Q^F(T) and Q^P are the activation energies in the ferromagnetic and paramagnetic state, respectively; s(T) is the ratio of the magnetization of pure iron at a given temperature T to that at 0K, and has been experimentally measured [14,15]; the constant α quantifies the extent of the influence of magnetic on activation energy. The measured value of α for Fe self-diffusion is 0.074, in the case of the solute species investigated in this context that have no measured α values available, the values can be estimated from a semi-empirical linear relationship with the induced change in local magnetization on Fe atoms in the first and second neighbor shells of a solute atom [16]. The first-principles calculations give direct access to the magnitude of the activation energy in the fully ordered ferromagnetic state 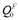(T=0K). Given the values of α and s(T), we can compute Q^P through the relation , and Q^F(T) from Eq. (1).

We based the diffusion calculations on the assumption that the mechanism of diffusion is primarily monovacancy mediated. For self-diffusion and solute diffusion on a bcc lattice, the diffusion coefficient can be expressed as following [10,17]:

D_self=a²f₀C_vw₀ (2)

D_solute=a²f₂C_vw₂(-ΔG_b/k_BT) (3)

where a is the bcc lattice constant, f₀=0.727 is the self-diffusion correlation factor, f₂ is the correlation factor for solute diffusion which depends on the relative jump rates for a vacancy to different sites neighboring the solute atom. C_v denotes the equilibrium vacancy concentration, can be written as C_v=exp(ΔS_f /k_B)exp(-ΔH_f /k_BT), where ΔS_f and ΔH_f are the vacancy formation enthalpy and entropy, respectively, the harmonic approximation makes these two become temperature-independent constants. and k_B is Boltzmann’s constant. w₀ and w₂ are the vacancy hopping frequencies for Fe and solute atoms to exchange with a nearest-neighbor vacancy, respectively. Based on transition state theory (TST), the vacancy hopping frequency w is written as , where and are the phonon frequencies in the initial state and transition state, and the product in the denominator ignores the unstable mode; ΔH_mig is the migration energy, gives the energy difference for the diffusing atom located at its initial equilibrium lattice position and the saddle-point position. The solute-vacancy binding free energy ΔG_b can be expressed as ΔG_b =ΔH_b–TΔS_b, where ΔH_b and ΔS_b are the binding enthalpy and entropy, respectively.

The correlation factor f₂ can be calculated using the nine-frequency model developed by Le Claire [11] which involves different jump frequencies of vacancies to their first neighbor position in the presence of the solute atoms, as illustrated in Fig. 1. In this model, the interaction of solute-vacancy is assumed up to second neighbor distance. The nine frequencies shown in Fig. 1 correspond to all of the distinct vacancy jumps, including the host Fe atom jump w₀ without impurity. The detailed calculation procedures could be found in Ref. [10].

Fig. 1. Schematic illustration of the nine-frequency model for the bcc Fe crystalline with a solute atom. The arrows indicate the direction of the vacancy jumps. The numbers in the circle represent the neighboring site of the solute atom.

For convenience, we can represent the self- and solute diffusion equations (Eqs.(2) and (3)) in Arrhenius form to obtain the pre-factor and activation energy of diffusion. By combining the above Eqs., the diffusion coefficient for Fe self-diffusion and solute diffusion can be expressed as:

(4)

For self-diffusion, the pre-factor is, and the activation energy in the fully ordered ferromagnetic state given as . Also, the solute diffusion coefficient can be expressed in an Arrhenius form with the pre-factor is, and.

The first-principles calculations presented here are carried out using the Vienna Ab Initio Simulation Package(VASP) with the projector augmented wave(PAW) method and the generalized gradient approximation of Perdew-Burke-Ernzerhof functional(GGA-PBE) [18]. The computations performed within a 4ï‚´4ï‚´4 supercell including 128 atoms. The binding, vacancy formation and migration energies were calculated with 300eV plane-wave cutoff and 12ï‚´12ï‚´12 k-point meshes. All calculations were performed spin polarized, with a ferromagnetic ordering of the Fe moments. The residual atomic forces in the relaxed configurations were lower than 0.01eV/Å. The transition states with the saddle point along the minimum energy diffusion path for vacancy migration were determined using nudged elastic band (NEB) method [19] as implemented in VASP. We adopt the harmonic approximation (HA) to consider the contribution of normal phonon frequencies to free energy. The normal phonon frequencies were calculated using the direct force-constant approach as implemented in the Alloy Theoretic Automated Toolkit (ATAT) [20] package. Similar cutoff energy, k-point mesh size and supercell size used for the total energies were used for the vibrational calculations.

3. Result and discussion

Table 1 illustrates our calculated vacancy formation, migration and binding energies, as well as the constant α for solute species, the associated activation energies for self- and solute-diffusion in the paramagnetic and fully ordered ferromagnetic state. For pure bcc Fe, the vacancy formation energy and migration energy obtained here are consistent with the reported range of values, ΔH_f=2.16-2.23 eV and ΔH_mig=0.55-0.64 eV [10,21,22]. For Y impurity in bcc Fe, the calculated vacancy binding energy and activation energy in full ordered ferromagnetic state also compare well with the previous first principles work [9,23], in which ΔH_b=-0.73 eV and =2.26 eV. It can be seen that Y and La have smaller activation energy than that for Fe self-diffusion, while Ce is predicted to have a lager value of activation energy than that for Fe self-diffusion, in both the ordered ferromagnetic and paramagnetic state.

Table 1

Vacancy formation energy ΔH_f , solute-vacancy binding energy ΔH_b, migration energy ΔH_mig, the ferromagnetic activation energy and the paramagnetic activation energy Q^P; the variable dependence parameter of activation energy on magnetization α (the value for Fe is taken from experimental measurements, while the values for Y, La and Ce have been estimated from first-principles calculations).

Solute-vacancy binding energy plays a crucial role in understanding solute diffusion kinetics. From Table 1 it can be seen that referring to the nearest-neighbor solute-vacancy pairs, the binding energies are all negative, which implies the solute-vacancy pairs are favorable. Specifically, Y and La impurities are computed to have higher values of solute-vacancy binding energies -0.69 eV and -0.66 eV, respectively, while that for Ce is -0.43 eV. To obtain information on the origin of these attractive behaviors, we decompose the total binding energy into the distortion binding energyand the electronic binding energy as [24] . The distortion binding energy is the energy that can be gained by reducing the distortion in the bcc Fe matrix when a solute atom and a vacancy combine to form a solute-vacancy pair, and can be expressed as:

(5)

where and can be calculated as follows: after the supercell containing a solute-vacancy pair (or a substitutional atom) has been fully relaxed, the solute-vacancy pair (or the substitutional atom) is removed from the system, then the total energy can be calculated. denotes the total energy of pure bcc Fe supercell, and is the total energy of the supercell containing a vacancy. Then can be calculated from . The calculated energy decomposition for solute-vacancy binding is shown in Table 2. The distortion energies (-0.31 to -0.65 eV) for all solute elements(Y, La and Ce) are negative, and much bigger than their corresponding electronic binding energies (-0.04 to -0.12 eV). This implies that the distortion energy is the major part of the total binding energy, i.e. the strain relief effect contribute significantly to the interaction between the impurity atom and the vacancy, especially for the solute Y and La, which accounted for 94.2% and 97.0% of the total binding energy, respectively.

Table 2

Decomposition of the total solute-vacancy binding energy into distortion binding energy and electronic binding energy.

The correlation factor f₂ is related to the probability of the reverse jump of a solute atom to its previous position [25]. Table 3 lists the calculated values of correlation factors for Y, La and Ce at representative temperatures of 850, 1000 and 1150K. The correlation factors for Ce is nearly a constant close to 1, while the Y and La diffusion correlation factors decrease with increasing temperature, corresponding to the weak solute-vacancy binding for Ce and the strong solute-vacancy binding for Y and La. Therefore, the Ce atom is the most difficult to return back to its original position in the temperature range of our investigation. Including the smallest binding energy, highest migration energy and correlation factor, provides an explanation for the low diffusivity of Ce atom.

Table 3

Correlation factors (f₂) for Y, La and Ce solute-diffusion at representative temperatures of 850, 1000 and 1150K.

Table 4 lists the calculated diffusion activation energies and pre-factors for Fe self-diffusion and Y, La and Ce impurity diffusion. For pure bcc Fe, we find our calculated results are in good agreement with the published values. For Y impurity in bcc Fe, the calculated activation energy in full ordered ferromagnetic state also compare well with the previous first principles work, while the pre-factor is as much as two orders of magnitude lager than the reported value. The experimental or calculated diffusion coefficients of La and Ce are not available to the best of our knowledge.

Fig. 2 presents a direct comparison between the calculated and published temperature dependent diffusion coefficients for Fe self-diffusion and Y solute diffusion. For Fe self-diffusion, the calculated values are in good agreement with Huang et al. [10] and Nitta et al.[24], but smaller than the measured data of Seeger [25], this discrepancy may be due to the impurity, defects and grain sizes of the testing materials, and instrumental accuracy. For Y solute diffusion, the diffusion coefficient values are higher by a factor of 4-5 than those due to Murali et al. [9], this discrepancy can be attributed to the harmonic vibration and the influence of the bulk magnetization on the activation energy.

The temperature dependence of the solute diffusion coefficients for Y, La and Ce in bcc Fe matrix are plotted in Fig. 3, where the Fe self-diffusion coefficient is also included. It can be clearly seen that the diffusion coefficients for Y and La are higher than the self-diffusion in pure bcc Fe, while the diffusion coefficients for Ce are lower than that of Fe self-diffusion, over the entire temperature range below the α-γ phase transition. For the case of Ce solute diffusivity, the lowest value of diffusion coefficient originates from the largest migration energy and the smallest solute-vacancy binding energy. For the two faster diffusers, Y and Ce, which have the comparable diffusion coefficients, we can observe that the diffusion rate of La is higher than that of Y at temperatures below 930 K, but this relation reverses with temperature rising above 930 K. This is attributed to the effects of the diffusion pre-factors of these two elements. Therefore, the investigation for diffusion should also be based on detailed considerations of the diffusion pre-factor, including the contribution of the correlation factor, rather than the vacancy formation energy and migration energy.

The diffusion properties of solute elements (Y, La and Ce) in bcc Fe matrix have been studied using DFT calculations in conjunction with the Le Claire nine-frequency model. Of the three impurities that we investigated, the diffusion coefficients for Y and La are comparable, and predicted to be larger than the Fe self-diffusion. In contrast, the calculated results indicate that Ce diffuse slower than Fe self-diffusion. The slowest diffusion rate of Ce originates from that the solute-vacancy binding energy for this element is lower than that of Y and La, and the former has higher migration energy as well. In the case of Y and La, the small direction deviation between the trends of the diffusion coefficients of these two impurities, mainly comes from the contribution of the diffusion correlation factor.

The authors are grateful for the financial support of the National Natural Science Foundation of China (No. 51101083) and the Natural Science Foundation of Inner Mongolia (No.2013MS0813).

References

[1] M.F. Yan, C.S. Zhang, Z. Sun, Appl. Surf. Sci. 289 (2014) 370.

[2] W. Hao, W.T. Geng, Nucl. Instrum. Meth. Phys. Res. B 280 (2012) 22.

[3] Y.H. Yoo, Y.S. Choi, J.G Kim, Y.S. Park, Corros. Sci. 52 (2010) 1123.

[4] S.K. Samanta, S.K. Mitra, T.K. Pal, Mater. Sci. Eng. A 430 (2006) 242.

[5] R. Thanneeru,S. Patil,S. Deshpande,S. Seal, Acta Mater. 55 (2007) 3457.

[6] S.T. Kim, S.H. Jeon, I.S. Lee, Y.S. Park, Corros. Sci. 52(2010) 1897.

[7] H.Z. Li, H.T. Liu, Z.Y. Liu, G.D.Wang, Mater. Charact. 103 (2015) 101.

[8] D. Simonovic, M.H.F. Sluiter, Phys. Rev. B 79 (2009) 054304.

[9] D. Murali, B.K. Panigrahi , M.C. Valsakumar, C.S. Sundar, J. Nucl. Mater. 419 (2011) 208.

[10] S.Y. Huang, D.L. Worthington, M. Asta, V. Ozolins, G. Ghosh, P. K. Liaw, Acta Mater. 58 (2010) 1982.

[11] A.D. Le Claire, Philos. Mag. 21 (1970) 819.

[12] S.Takemoto, H. Nitta, Y. ijima, Y.Yamazaki, Philos. Mag. 87 (2007) 1619.

[13] L. Ruch, D.R. Sain, H.L. Yeh, L.A. Girifalco, J. Phys. Chem. Solids 37 (1976) 649.

[14] H.H. Potter, Proc. R. Soc. London, Ser. A 146 (1934) 362.

[15] J. Crangle, G.M. Goodman, Proc. R. Soc. London, Ser. A 321 (1971) 477.

[16] S. Takemoto, H. Nitta, Y. Iijima, Y. Yamazaki, Philos. Mag. 87 (2007) 1619.

[17] M. Mantina, Y. Wang, R. Arroyave, L.Q. Chen, Z.K. Liu, Phys. Rev. Lett. 100 (2008) 215901.

[18] G. Kresse, J. Hafner, Phys. Rev. B 47 (1993) 558.

[19] G. Henkelman, H. Jonsson, J.Chem. Phys. 113 (2000)9978.

[20] A. van de Walle,M. Asta,G. Ceder, Calphad 26 (2002) 539.

[21] C. Zhang, J. Fu, R.H. Li, P.B. Zhang, J.J. Zhao, C. Dong, J. Nucl. Mater. 455 (2014) 354.

[22] H. Ullmaier, Atomic Defects in Metals, Springer, Berlin Heidelberg, 1991.

[23] O.I. Gorbatov, P.A. Korzhavyi, A.V. Ruban, B. Johansson, Yu.N. Gornostyrev, J. Nucl. Mater. 419 (2011) 248.

[24] X.S. Kong, X.B. Wu, Y.W. You, C.S. Liu, Q.F. Fang, J.L. Chen, G.N. Luo, Z.G. Wang, Acta Mater. 66 (2014) 172.

[25] M. Mantina, Y. Wang, L.Q. Chen, Z.K. Liu, C. Wolverton, Acta Mater. 57 (2009) 4102.

[26] H. Nitta, T. Yamamoto, R. Kanno, K. Takasawa, T. Iida, Y. Yamazaki, S. Ogu, Y. Iijima, Acta Mater. 50 (2002) 4117.

[27] A. Seeger, Phys. Status Solidi A 167 (1998) 289.