Experiment to Study Conservation of Energy
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 1418 words | ✅ Published: 01 Feb 2018 |
Conservation of Energy
- Osamah Nuwisser
Abstract:
The purpose of this experiment was to study the conservation of energy. We considered all type of energies present in our system (KE and PE) to compute total energy at any instant during the experiment. We accomplish two tasks: first we verified the conservation of total energy during single step of the movement of the glider over the ramp and then we compared total energy of several consecutive up and down motions to check whether the collision of glider with the bumper at the lower end of the ramp was elastic or inelastic. For first task, we found that kinetic energy increases as potential energy decreases during downward motion of the glider but the total energy remains almost constant. For the second task, we found that the total energy of each step was less than that of the preceding one. This tells us that the collision between the glider and the bumper was inelastic due to which we have a net energy loss. We also increased height and mass of the glider and found that as a consequence the coefficient of restitution decreases. Arbitrariness of PE is also described.
Introduction:
According to the law of energy conservation:
Energy can neither be created nor destroyed; however it can be converted from one form of energy to the other.
Also, we know that energy is conserved in elastic collision. Obviously, a loss in energy during a collision will imply that the collision was inelastic. In this experiment, we accomplished two tasks in which were able to verify/use the two mentioned facts.
For the first task, we simply observed that during the first downward motion of the glider the total energy remained constant throughout the motion. Also, in our system there are only two types of energy involved: kinetic energy and potential energy. Thus
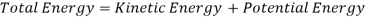

Therefore, for the total energy to remain constant it is necessary that the kinetic energy increases as the potential energy decreases due to downward motion of the glider. This can easily be observed if we plot the three curves, total energy, kinetic energy and potential energy, in one graph for downward motion of the glider.
For the second task, we recorded the same data for a few consecutive upward and downward motions of the glider. By comparing the amount of total energy for each step, we can tell whether the collision between the glider and the bumper was elastic or inelastic. If the total energy of each step is less than that of its preceding step, the collision is inelastic.
Coefficient of Restitution:- For our case, it is defined as

Its value can be in [0, 1]. In case of 0 the glider will be at rest after collision, in case of 1 the collision will be elastic. For intermediate values, collision will be inelastic with glider in motion after the collision.
Experimental Description:
The apparatus consisted of a glider which was moved on a tilted ramp with a bumper at the lower end. This set up was connected to the computer where the appropriate software recorded the required quantities.
The glider was kept at the top of ramp at rest. Then it was allowed to move under gravity. It moved until it reached near the ground level where it hit the bumper and was reversed to move up the ramp where it stopped at certain height and then moved down again and so on. We stoped the data storage in the computer after about 10s. We repeated the experiment two time varying height and then mass. We took 3 readings in each case.

Figure i: An Experimental Set -up
Data and Analysis:
Run 24: 2014-10-30 17:08:53



Figure ii: Position, Velocity & Energy vs Time
Data of position, velocity and energy (total, kinetic and potential) was plotted in the computer by the software against time (see figure ii above). PE was defined to be zero on ground level. For first task, we need to examine the variation of energy during first 2.5s. In start, PE is the maximum and KE is zero. As the glider moves down on the ramp, PE decreases and KE increases gradually. But we see that PE is not zero at its minimum. This non-zero minimum value is the value of the PE at the small height when it collides with the bumper.

Figure iii: A Comparison of KE, PE & ME
We also find that the total energy is not conserved at the point of collision where we see a loss in total energy (annihilation of energy).
For second task, we compare the values of the total mechanical energy for each cycle with that of the preceding one. It is evident from the graph of energy that this energy decreased suddenly after each collision. Thus the collision was inelastic. Also, we can see from the previous graphs that total energy of the glider was zero at certain instant after collision; the glider collided with the bumper, imparted its all (kinetic) energy to the bumper and came to the rest. Then bumper shifted a fraction of this energy to the glider in form of KE forcing it to move in the opposite direction (up the ramp).
To read total energy as zero at certain point, we can construct the following simplest case. Consider the glider to be at rest at a height from the ground on the ramp (say 80cm). Obviously, KE is zero. We define the origin at this point. So its height w.r.t. origin becomes zero. Now we measure PE with reference to the same point (because of arbitrariness of PE) which becomes  . Thus the total energy at this point is zero. As far as the conservation of energy is concerned, that is satisfied because we have defined origin at the highest point. As the glider moves down the ramp, value of h becomes negative. This negative value of PE annihilates the positive value of KE that is produced due to increasing velocity. Thus the total energy remains zero. Another way of doing the same is to define PE to be zero at the highest point, measure height as positive and add a minus sign with the formula for the PE in the equation of the total energy.
. Thus the total energy at this point is zero. As far as the conservation of energy is concerned, that is satisfied because we have defined origin at the highest point. As the glider moves down the ramp, value of h becomes negative. This negative value of PE annihilates the positive value of KE that is produced due to increasing velocity. Thus the total energy remains zero. Another way of doing the same is to define PE to be zero at the highest point, measure height as positive and add a minus sign with the formula for the PE in the equation of the total energy.

To study the variation in the coefficient of restitution, we chose two continuous parameters: height and mass of the glider. We took 3 readings because the tendency of increasing/decreasing should not be study by taking the minimum possible, 2, readings due of the possibility of error. The data is given in the following table.
Table 1

The following plot shows coefficient of restitution vs height.

Figure iv: Coefficient of Restitution vs Height
Second and third readings show that the coefficient of restitution decreases with increasing the height. But the first two readings tell the reverse. However, by considering the error bars of first two points we can conclude that:
“Coefficient of restitution decreases with increasing height.”
The following plot shows coefficient of restitution-mass vs mass.

Figure v: Coefficient of Restitution Mass vs Mass
This tells us clearly that:
“Coefficient of restitution decreases with increasing mass.”
Results and Conclusion:
- For task 1: we have found that total energy remains constant during the motion of the glider until the collision occurs. Thus law of conservation is verified and its limitation (inelastic collision) is found.
- For task 2: By comparing the total energy before collision with the total energy after collision, we conclude that the collision is inelastic. Also, we showed that by using the arbitrariness of the value of PE we can set the total energy of a sliding object to be zero.
- By varying two continuous parameters mass of the glider and initial height of the glider, we found that increasing any one of them leads to a decrease in the value of coefficient of restitution. Since smaller value of coefficient of restitution means greater loss of energy, we conclude that: by increasing height or by increasing mass, more energy is lost during the collision. The physical reasoning behind this conclusion can be understood. In both the cases, increasing height or increasing mass, the maximum PE (mgh) increases. This entire maximum PE becomes maximum KE just before the collision. Thus more energy is lost during the collision.
References:
- Air Track and Cart (1996). Available from: [Online] http://demo.physics.uiuc.edu/LectDemo/scripts/demo_descript.idc?DemoID=110
- Energy Conservation on an Incline. Available from: [Online] http://www.physicsclassroom.com/mmedia/energy/ie.cfm
- Coefficient of Restitution (2014). Available from: [Online] http://en.wikipedia.org/wiki/Coefficient_of_restitution
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


