Electronic Structure and Spontaneous Polarization in BiFeO3

Electronic structure and spontaneous polarization in multiferroic bulk BiFeO₃

Z. Mahhouti ^1,2,3,* , H. El Moussaoui ¹ , M. Hamedoun ¹ , M. El Marssi ³ , A. Lahmar ² , A. El Kenz ² , and A. Benyoussef ^1,2,4

Abstract:

The electronic structure, magnetic properties and spontaneous polarization in Bismuth ferrite BiFeO₃ are investigated using first-principle calculations. The computed results show that the ground state of bulk BiFeO3 is rhombohedral R3c symmetry with G-type antiferromagnetic ordering and insulating, the computed results are in good agreement with available experiments. The electronic structure has been studied using the full potential linearized augmented plane wave (FP-LAPW) method within generalized gradient approximation (GGA) and modified Becke-Johnson potential (mBJ). Therefore, the finding band gap value is equal to the experimental value (E_g=2.5 eV) and much better than other theoretical values, the local magnetic moment at the Fe atoms reaches the experimental value and it is in good agreement with previously reported theoretical, with the large atomic displacement the modern theory of polarization predicts a large spontaneous polarization in multiferroic bulk BiFeO₃.

1. INTRODUCTION

The multiferroic term denotes the coexistence of several ferroic orders (ferroelectric, ferromagnetic, and ferroelastic) in one material[1], coupled or not. Multiferroic materials are very rare because the origins of ferroelectricity and ferromagnetism are hardly compatible as shown by Hill et al.[2][3]. However, there are some exceptions such as La_0.1Bi_0.9MnO₃ which is ferroelectric below 770 K and ferromagnetic below 105 K[4]. The definition of multiferroic has therefore been extended to materials with antiferroic orders such as BiFeO₃ which is ferroelectric and antiferromagnetic.     

Bismuth ferrite BiFeO₃ (BFO) is one of the few magnetoelectric multiferroics who has simultaneously ferroelectric and antiferromagnetic orders under ambient conditions of temperature and pressure. Indeed, its high Curie temperature (T_C = 1103 K)[5] and Néel temperature (T_N = 643 K)[6] provide a wide range of applications at different temperatures[7] such as spintronics, data storage and microelectronic devices[8][9], In addition, a magnetoelectric coupling is possible at room temperature.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

Recently, BFO has seen a considerable increase in interest since the discovery of a much better spontaneous polarization, greater than 150 µC/cm², when the material is grown in thin layers[10]. This discovery aroused great enthusiasm among the scientific community who wanted to explain the origin of some phenomenon and explore this material again.

The phase diagram established according to the reference[11] shows the succession of three phases with increasing of temperature denoted , ,and , respectively. In its bulk form and at room temperature, BFO has a distorted perovskite structure with rhombohedral symmetry and space group R3c (a = b = c = 5.63 Å,  = 59.4°)[12][8]. The primitive unit cell contains two formula units (ten atoms), each Fe atom is surrounded by six antiparallel spin neighbors, the magnetic moments are oriented perpendicularly to the [111] direction, which leads to develop a G-type antiferromagnetic order on the whole of the material. However, new observations have revealed that the direction in which antiferromagnetism manifests rotates through the crystal[13]. This noncollinearity propagates within the material with a period from 620 Å to 640 Å[13][14] and superimposes on the G-type antiferromagnetic order. As the noncollinearity is quite minimal, the simplification to a collinear magnetic structure is possible[15]. In this paper, the noncollinearity effects were not taken during our calculations.

Since BFO is grown as a thin layers, the material may undergo a compressive or extensive stress due to the difference between the primitive cell of the material in its bulk form and those of the monocrystalline substrate, the small grown thickness is able to accept any relaxation of the structure. This can cause changes in the structure parameters of the crystal compared to its bulk form. However, other experimental works[16][17] showed that even BFO grown in thin layers, retains its rhombohedral symmetry.

For a long time BFO considered too low to be exploitable ( Ps = 6.1 µC/cm² ) according to the first measurements of Teague et al.[5], the ferroelectricity of BFO was studied again following the results of Young et al.[10] on thin layers of BFO ( Ps = 158 µC/cm²). However, many experimental studies carried out during this period gave a confusing results, the spontaneous polarization varying from 2.2 µC/cm² [18] to 158 µC/cm² [10]. The study of the ferroelectricity of BFO is a concrete example to combine experimental results and theoretical calculations. In this case, the calculation methods allow to explain the difference between the first measured values of bulk BFO and those obtained on the same material grown in thin layers.

In this paper, we study in detail the magnetic properties of bulk BFO, while considering a G-type antiferromagnetic order. But it is necessary to determine first the electronic configuration and to calculate the band gap, in order to understand and obtain the theoretical model which corresponds to the reality of the material, and then to determine the spontaneous polarization using modern theory of polarization.

2. METHOD

The calculations which we present in the remainder of this paper use the density functional theory (DFT) implemented in WIEN2k code. The interactions between electrons and ions are described in the framework of full potential linearized augmented plane wave (FP-LAPW) method. As the 3d electrons in transition -metal Fe atom are incompletely filled, the spin density approximation was employed withinstry the Perdew-Burke-Ernzerhof (PBE) form of the generalized gradient approximation (GGA) and modified Becke-Johnson potential (mBJ). The new version of the exchange potential, proposed for the first time by the Becke and Johnson[19], was recently published by Tran and Blaha[20]. The modified Becke-Johnson potential (mBJ) proposed by Tran and Blaha is:

With 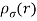is the electronic density, is kinetic energy density and 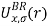is the potential of Becke-Roussel. In this work, the mBJ potential is used in combination with the GGA-PBE approximation to compute the electronic structure, magnetic properties and spontaneous polarization in multiferroic bulk BFO. Our calculations do not include the spin-orbit interactions and the noncollinearity effects. The mesh of the first Brillouin zone in the reciprocal space was carried out using a 4 x 4 x 4 Monkhorst-Pack k-points grid. The structural parameters of BFO in space group R3c ( i.e, the lattice constant and atomic positions ) are considered as calculated by Wang et al.[8] as given from Kubel et al.[12]. The results of relaxing the cell volume, rhombohedral angle, and atomic positions within the R3c symmetry in reference[8] show that there is an alternation of Bi³⁺ and Fe³⁺ ions along the [111] axis; Each of these atoms is surrounded by six oxygen atoms, which thus form an octahedron around each cation. Inside the octahedron FeO₆, the Fe³⁺ ion is outside the FeO₂ plane (forming the base of the octahedron), which leads a distortion of the octahedron.

The calculation of the spontaneous polarization using the modern theory of polarization is carried out by determining the difference in polarization between two symmetry (The non-centrosymmetric phase R3c which is ferroelectric and the centrosymmetric phase R-3c supposed paraelectric). In order to evaluate the polarization of the structure studied, we must therefore use a structure (centrosymmetric) as a reference with the same unit cell as the real structure (non-centrosymmetric), but its atomic positions do not induce electrical dipoles. Energetically, these two structures are very close, which confirms our choice of R-3c symmetry as a centrosymmetric reference. They differ by the addition of a center of inversion within the symmetry, and the passage from one symmetry to the other is due to the displacement of the atoms along the [111] direction which is accompanied with a rotation of the FeO₆ octahedra perpendicular to the same direction. This evolution of the paraelectric phase to the ferroelectric phase allows us to explain the birth of ferroelectricity within the bismuth ferrite BFO and to reproduce it efficiently in our calculations. The modern theory of polarization was applied for the first time to compute the ferroelectricity within the cubic perovskite-type KNbO₃. The results obtained ( P = 35 µC/cm² [21][22]) showed excellent agreement with the experimental data ( P = 37 µC/cm²[23]). Other studies were carried out subsequently, confirming the reliability of this method with respect to the experimental reality. Today, the modern theory of polarization is widely used.

3. Results and Discussion

1. Electronic and magnetic properties

In this section, we study the electronic structure of bulk BFO in ferroelectric R3c structure, considering the relaxing values of cell parameter, rhombohedral angle and atomic positions by Wang et al.[8]. We computed and plotted the band structure and electronic state densities with the same parameters mentioned at the paragraph II. The band gap value are calculated using mBJ potential in combination with the GGA-PBE approximation, our calculated band gap value is the same as the value measured by Gao et al.[24] from the UV-visible diffuse reflectance spectrum witch is equal to 2.5 eV, our computed band gap is much better than other theoretical works such as Neaton et al.[15] who found an indirect band gap of 0.4, 1.3, and 1.9 eV using LSDA+U approximation with U=0, 2, and 4 eV, respectively. The same for Tütüncü et al.[25] they found an indirect band gap of 0.9, 1.4, and 2.1 eV using LSDA+U approximation with U=0, 2, and 4 eV, respectively. Our band structure results (Fig.1) indicate an indirect band gap of approximately 2.5 eV witch is in excellent agreement to the experimental measurement of about 2.5 eV [24][26]. Therefore, this equality between our calculated band gap and the experimental value confirms the insulating character of bulk BFO.

In order to understand why the magnetic moments of the Fe atoms were arranged antiparallel within bulk BFO, we relaxed it according to different magnetic configurations: paramagnetic, ferromagnetic, and antiferromagnetic. The ground-state energy of the various possible magnetic configurations shows that the G-type antiferromagnetic configuration is the one which offers the material its greatest stability.

FIG. 1. Calculated band structure for rhombohedral BiFeO₃.

FIG. 2. Calculated total density of states for rhombohedral BiFeO₃.

Calculated density of state (Fig.2) for R3c BFO indicates an identical distribution between electronic states “up” and “down”, which clearly exhibits the antiferromagnetic order of the material, in this case the antiferromagnetic order can only be G-type. The Fe atoms along the [111] axis have a local magnetic moment of 4.02 μ_B comes from 3d states, this value is much better than 4.25 μ_B and 4.17 μ_B reported by Tütüncü et al.[25] using LSDA+U with U = 4 and 6 eV, respectively. Therefore, our computed local magnetic moment of Fe atoms is very close to the measurement value of about 3.75μ_B [27].

FIG. 3. Atomic projection of electronic PDOS for rhombohedral BiFeO₃.

Figure 3 shows atomic projected electronic density of states (PDOS) around the ban gap region for both spin channels. The results suggest that the valence band are predominantly formed by Fe 3d states, hybridized with a contribution from O 2p states. Conduction band states are occupied by a large amount of Fe 3d states, hybridized with a small contribution of Bi 6p states that also contains a significant amount of O 2p states.

4. Spontaneous polarization

The spontaneous polarization was calculated within bulk BFO using the ferroelectric structure R3c and the hypothetical centrosymmetric phase R-3c. The centrosymmetric phase must be judiciously chosen, in order to found the difference of ferroelectric polarization between the centrosymmetric and non-centrosymmetric phases less than the quantum of polarization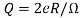, Where 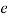is the electronic charge, 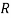is a lattice vector in the direction of polarization, and 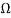is the volume of the unit cell. Our calculations have shown that centrosymmetric phase R-3c is the structure closest to the ferroelectric structure R3c, both energetically as well as structural. This symmetry differs from the R3c only by the addition of a center of inversion. The transition from the paraelectric to the ferroelectric phase was characterized by a large displacement of the atoms along the [111] axis and a rotation of the FeO₆ octahedra. Therefore, we expect that the spontaneous polarization develops along the [111] axis. In order to calculate the difference of polarization, we have considered that the transition from paraelectric to ferroelectric phase was done adiabatically and continuously. In this way, each atom moves along a path divided into segments of equal length. This method allowed us to follow the evolution of the spontaneous polarization during the whole paraelectric-ferroelectric transition. Throughout the paraelectric-ferroelectric transition, it is imperative to avoid any external contribution to symmetry, such as compression or expansion of the unit cell (in this case we do not calculate the real spontaneous polarization). For this reason, the structures used for our calculations have the same cell parameters, only the atomic positions were shifted.

The modern theory of polarization compute the both, ionic and electronic contribution to the spontaneous polarization using the sum of the Wannier centers of the occupied bands. Our results showed that the spontaneous polarization developed along three directions, and was 58.8 µC/cm² along each axis, resulting a spontaneous polarization of 101.1 µC/cm² along the [111] axis which is in full agreement with the spontaneous polarization calculated by Neaton et al.[15] using LSDA+U. Early measurements on bulk BFO single crystals[5] found a small polarization of about 6.1 µC/cm². On the other hand, many experiment studies on thin film samples of BFO showed a large spontaneous polarization of about 100-158 µC/cm² [16][10]. The anomalously early value was caused by several explanations. First, the authors[5] indicated that their hysteresis loops were not saturated. Second, maybe the small value limited by the poor of the sample quality. Finally, the third explanation is that the crystal structure is not the same. Recently, Lebeugle et al.[28] have prepared a highly pure BFO single crystal (bulk BFO with a rhombohedral R3c symmetry) and measured the spontaneous polarization, they found a very large value of about 100 µC/cm² [28] which is an intrinsic property of the bulk BFO, as expected by our theoretical studies.

5. CONCLUSIONS

In summary, Bismuth ferrite BiFeO₃ is one of a few magnetoelectric multiferroics who has simultaneously ferroelectric and ferromagnetic orders, it has seen a considerable increase in interest since the discovery of a high spontaneous polarization. The first principle calculations with our approximations and parameters chosen allowed us to understand and obtain the behaviors of electronic and magnetic properties which make possible the computing of the right band gap and local magnetic moment. The property intrinsic of the large spontaneous electric polarization in bulk BiFe₂O₃ showed by recently experiment studies was confirmed by our theoretical investigations using the modern theory of polarization. These good agreements between our theoretical investigation and experimental measurement allow the scientific community to compute other properties and understand the physics behind the measurement at the atomic level.

References

[1]H. Schmid, “Multi-ferroic magnetoelectrics,” Ferroelectrics, vol. 162, no. 1, pp. 317-338, Jan. 1994.

[2]N. A. Hill, “Why Are There so Few Magnetic Ferroelectrics?,” J. Phys. Chem. B, vol. 104, no. 29, pp. 6694-6709, Jul. 2000.

[3]N. A. Hill, “Density Functional Studies of Multiferroic Magnetoelectrics,” Annu. Rev. Mater. Res., vol. 32, no. 1, pp. 1-37, Aug. 2002.

[4]A. Moreira dos Santos et al., “Orbital ordering as the determinant for ferromagnetism in biferroic BiMnO 3,” Phys. Rev. B, vol. 66, no. 6, Aug. 2002.

[5]J. R. Teague, R. Gerson, and W. J. James, “Dielectric hysteresis in single crystal BiFeO3,” Solid State Commun., vol. 8, no. 13, pp. 1073-1074, 1970.

[6]G. A. Smolenskii and I. E. Chupis, “Ferroelectromagnets,” Phys.-Uspekhi, vol. 25, no. 7, pp. 475-493, Jul. 1982.

[7]M. Fiebig, “Revival of the magnetoelectric effect,” J. Phys. Appl. Phys., vol. 38, no. 8, pp. R123-R152, Apr. 2005.

[8]J. Wang, “Epitaxial BiFeO3 Multiferroic Thin Film Heterostructures,” Science, vol. 299, no. 5613, pp. 1719-1722, Mar. 2003.

[9]Y. Tokura, “MATERIALS SCIENCE: Multiferroics as Quantum Electromagnets,” Science, vol. 312, no. 5779, pp. 1481-1482, Jun. 2006.

[10]K. Y. Yun, D. Ricinschi, T. Kanashima, M. Noda, and M. Okuyama, “Giant ferroelectric polarization beyond 150 μC/cm2 in BiFeO3 thin film,” Jpn. J. Appl. Phys., vol. 43, no. 5A, p. L647, 2004.

[11]R. Palai et al., “β phase and γ ˆ’ β metal-insulator transition in multiferroic Bi Fe O 3,” Phys. Rev. B, vol. 77, no. 1, Jan. 2008.

[12]F. Kubel and H. Schmid, “Structure of a ferroelectric and ferroelastic monodomain crystal of the perovskite BiFeO3,” Acta Crystallogr. B, vol. 46, no. 6, pp. 698-702, Dec. 1990.

[13]I. Sosnowska, T. P. Neumaier, and E. Steichele, “Spiral magnetic ordering in bismuth ferrite,” J. Phys. C Solid State Phys., vol. 15, no. 23, p. 4835, 1982.

[14]D. Lebeugle, D. Colson, A. Forget, M. Viret, A. M. Bataille, and A. Gukasov, “Electric-Field-Induced Spin Flop in BiFeO 3 Single Crystals at Room Temperature,” Phys. Rev. Lett., vol. 100, no. 22, Jun. 2008.

[15]J. B. Neaton, C. Ederer, U. V. Waghmare, N. A. Spaldin, and K. M. Rabe, “First-principles study of spontaneous polarization in multiferroic Bi Fe O 3,” Phys. Rev. B, vol. 71, no. 1, Jan. 2005.

[16]J. Li et al., “Dramatically enhanced polarization in (001), (101), and (111) BiFeO3 thin films due to epitiaxial-induced transitions,” Appl. Phys. Lett., vol. 84, no. 25, pp. 5261-5263, Jun. 2004.

[17]G. Xu, H. Hiraka, G. Shirane, J. Li, J. Wang, and D. Viehland, “Low symmetry phase in (001) BiFeO3 epitaxial constrained thin films,” Appl. Phys. Lett., vol. 86, no. 18, p. 182905, May 2005.

[18]V. R. Palkar, J. John, and R. Pinto, “Observation of saturated polarization and dielectric anomaly in magnetoelectric BiFeO3 thin films,” Appl. Phys. Lett., vol. 80, no. 9, pp. 1628-1630, Mar. 2002.

[19]A. D. Becke and E. R. Johnson, “A simple effective potential for exchange,” J. Chem. Phys., vol. 124, no. 22, p. 221101, Jun. 2006.

[20]F. Tran and P. Blaha, “Accurate Band Gaps of Semiconductors and Insulators with a Semilocal Exchange-Correlation Potential,” Phys. Rev. Lett., vol. 102, no. 22, Jun. 2009.

[21]R. Resta, M. Posternak, and A. Baldereschi, “Towards a quantum theory of polarization in ferroelectrics: The case of KNbO 3,” Phys. Rev. Lett., vol. 70, no. 7, p. 1010, 1993.

[22]R. Resta, M. Posternak, and A. Baldereschi, “First-Principles Theory of Polarization in Ferroelectrics,” in MRS Proceedings, 1992, vol. 291, p. 647.

[23]W. Kleemann, F. J. Schäfer, and M. D. Fontana, “Crystal optical studies of spontaneous and precursor polarization in KNbO 3,” Phys. Rev. B, vol. 30, no. 3, p. 1148, 1984.

[24]F. Gao et al., “Preparation and photoabsorption characterization of BiFeO3 nanowires,” Appl. Phys. Lett., vol. 89, no. 10, p. 102506, Sep. 2006.

[25]H. M. Tütüncü and G. P. Srivastava, “Electronic structure and zone-center phonon modes in multiferroic bulk BiFeO3,” J. Appl. Phys., vol. 103, no. 8, p. 083712, Apr. 2008.

[26]T. Kanai, S. Ohkoshi, and K. Hashimoto, “Magnetic, electric, and optical functionalities of (PLZT) x (BiFeO 3) 1- x ferroelectric-ferromagnetic thin films,” J. Phys. Chem. Solids, vol. 64, no. 3, pp. 391-397, 2003.

[27]I. Sosnowska, W. Schäfer, W. Kockelmann, K. H. Andersen, and I. O. Troyanchuk, “Crystal structure and spiral magnetic ordering of BiFeO 3 doped with manganese,” Appl. Phys. Mater. Sci. Process., vol. 74, no. 0, pp. s1040-s1042, Dec. 2002.

[28]D. Lebeugle, D. Colson, A. Forget, and M. Viret, “Very large spontaneous electric polarization in BiFeO3 single crystals at room temperature and its evolution under cycling fields,” Appl. Phys. Lett., vol. 91, no. 2, p. 022907, Jul. 2007.