Effect of Short Range Correlation
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 2519 words | ✅ Published: 15 Sep 2017 |
The effect of short range correlation on the nuclear charge density distribution, elastic and inelastic electron scattering coulomb form factors of 16O nucleus
Abdullah S. Mdekil
Abstract
The effect of the short range correlation on the charge density disribution, elastic electron scattering form factors and inelastic Coulomb form factors is studied for the two excited 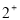 states (6.92 and 11.52 MeV) in
states (6.92 and 11.52 MeV) in 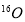 is analyzed. This effect (which depends on the correlation parameter
is analyzed. This effect (which depends on the correlation parameter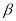 ) is inserted into the ground state charge density distribution through the Jastrow type correlation function. The single particle harmonic oscillator wave function is used with an oscillator size parameter
) is inserted into the ground state charge density distribution through the Jastrow type correlation function. The single particle harmonic oscillator wave function is used with an oscillator size parameter 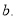 The parameters
The parameters 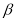 and
and 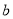 are considered as free parameters, adjusted for each excited state separately so as to reproduce the experimental root mean square charge radius of
are considered as free parameters, adjusted for each excited state separately so as to reproduce the experimental root mean square charge radius of 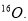 In inelastic coulomb (longitidinal) form factors of 16O, two different models are employed for
In inelastic coulomb (longitidinal) form factors of 16O, two different models are employed for 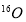 . In the first model (model A),
. In the first model (model A), 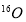 is considered as a closed shell nucleus. Here, the model space in
is considered as a closed shell nucleus. Here, the model space in 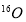 does not contribute to the transition charge density, because there are no protons outside the closed shell nucleus
does not contribute to the transition charge density, because there are no protons outside the closed shell nucleus 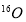 . In the second model (model B), the nucleus of
. In the second model (model B), the nucleus of 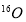 is assumed as a core of
is assumed as a core of 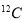 with 2 protons and 2 neutrons move in
with 2 protons and 2 neutrons move in 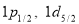 and
and 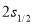 model space. It is found that the introduction of the effect of short range correlations is necessary for obtaining a remarkable modification in the calculated inelastic Coulomb form factors and considered as an essential for explanation the data amazingly throughout the whole range of considered momentum transfer.
model space. It is found that the introduction of the effect of short range correlations is necessary for obtaining a remarkable modification in the calculated inelastic Coulomb form factors and considered as an essential for explanation the data amazingly throughout the whole range of considered momentum transfer.
Keywords: charge density distribution, elastic charge form factors, inelastic longitudinal form factors, short range correlation.
1-Introduction
Electron scattering provides more accurate information about the nuclear structure for example size and charge distribution. It provides important knowledge about the electromagnetic currents inside the nuclei. Electron scattering have been provided a good test for such evaluation since it is sensitive to the spatial dependence on the charge and current densities [1, 2, 3].
Depending on the electron scattering, one can distinguish two types of scattering: in the first type, the nucleus is left in its ground state, that is called “elastic electron scattering” while in the second type, the nucleus is left on its different excited states, this is called “inelastic electron scattering” [4, 5].
In the studies of Massen et al. [6-8], the factor cluster expansion of Clark and co-workers [9-11] was utilized to derive an explicit form of the elastic charge form factor, truncated at the two-body term. This form, which is a sum of one- and two-body terms, depends on the harmonic oscillator parameter and the correlation parameter through a Jastrow-type correlation function [12]. This form is employed for the evaluation of the elastic charge form factors of closed shell nuclei 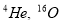 and
and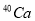 in an approximate technique (that is, for the expansion of the two-body terms in powers of the correlation parameter, only the leading terms had been kept) for the open
in an approximate technique (that is, for the expansion of the two-body terms in powers of the correlation parameter, only the leading terms had been kept) for the open 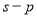 and
and 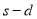 shell nuclei. Subsequently, Massen and Moustakidis [13] performed a systematic study of the effect of the SRC on
shell nuclei. Subsequently, Massen and Moustakidis [13] performed a systematic study of the effect of the SRC on 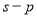 and
and 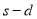 shell nuclei with entirely avoiding the approximation made in their earlier works outlined in [6-8] for the open shell nuclei. Explicit forms of elastic charge form factors and densities were found utilizing the factor cluster expansion of Clark and co-workers and Jastrow correlation functions which introduce the SRC. These forms depends on the single particle wave functions and not on the wave functions of the relative motion of two nucleons as was the case of our previous works [14-20] and other works [6,21,22].
shell nuclei with entirely avoiding the approximation made in their earlier works outlined in [6-8] for the open shell nuclei. Explicit forms of elastic charge form factors and densities were found utilizing the factor cluster expansion of Clark and co-workers and Jastrow correlation functions which introduce the SRC. These forms depends on the single particle wave functions and not on the wave functions of the relative motion of two nucleons as was the case of our previous works [14-20] and other works [6,21,22].
It is important to point out that all the above studies were concerned with the analysis of the effect of the SRC on the elastic electron scattering charge form factors of nuclei.
There has been no detailed investigation for the effect of the SRC on the inelastic electron scattering form factors of nuclei. We thus, in the present work, perform calculations with inclusion this effect on the inelastic Coulomb form factors for closed shell nucleus. As a test case, the 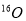 is considered in this study. To study the effect of SRC (which depends on the correlation parameter
is considered in this study. To study the effect of SRC (which depends on the correlation parameter 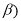 on the inelastic electron scattering charge form factors of considered nucleus, we insert this effect on the ground state charge density distribution through the Jastrow type correlation function [12]. The single particle harmonic oscillator wave function is used in the present calculations with an oscillator size parameter
on the inelastic electron scattering charge form factors of considered nucleus, we insert this effect on the ground state charge density distribution through the Jastrow type correlation function [12]. The single particle harmonic oscillator wave function is used in the present calculations with an oscillator size parameter 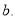 The effect of SRC on the inelastic Coloumb form factors for the two excited
The effect of SRC on the inelastic Coloumb form factors for the two excited 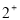 states (6.92 and 11.52 MeV) in
states (6.92 and 11.52 MeV) in 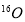 is analyzed.
is analyzed.
2. Theory
Inelastic electron scattering longitudinal (Coulomb) form factor involves angular momentum 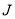 and momentum transfer
and momentum transfer 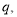 and is given by [23]
and is given by [23]
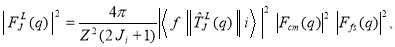 (1)
(1)
where 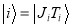 and
and 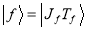 are the initial and final nuclear states (described by the shell model states of spin
are the initial and final nuclear states (described by the shell model states of spin 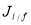 and isospin
and isospin 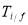 ),
), 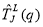 is the longitudinal electron scattering operator,
is the longitudinal electron scattering operator, 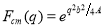 is the center of mass correction (which removes the spurious states arising from the motion of the center of mass when shell model wave function is used),
is the center of mass correction (which removes the spurious states arising from the motion of the center of mass when shell model wave function is used), 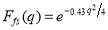 is the nucleon finite size correction and assumed to be the same for protons and neutrons, A is the nuclear mass number,
is the nucleon finite size correction and assumed to be the same for protons and neutrons, A is the nuclear mass number, 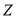 is the atomic number and
is the atomic number and 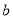 is the harmonic oscillator size parameter.
is the harmonic oscillator size parameter.
The form factor of eq.(1) is expressed via the matrix elements reduced in both angular momentum and isospin [24]
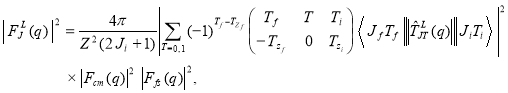 (2)
(2)
where in eq. (2), the bracket ( ) is the three-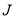 symbol, where
symbol, where 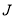 and
and 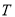 are restricted by the following selection rule:
are restricted by the following selection rule:
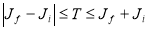
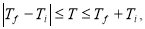 (3)
(3)
and 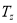 is given by
is given by 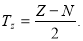
The reduced matrix elements in spin and isospin space of the longitudinal operator between the final and initial many particles states of the system including configuration mixing are given in terms of the one-body density matrix (OBDM) elements times the single particle matrix elements of the longitudinal operator [25]
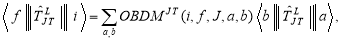 (4)
(4)
where 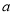 and
and 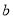 label single particle states (isospin included) for the shell model space. The
label single particle states (isospin included) for the shell model space. The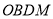 in eq. (4) is calculated in terms of the isospin-reduced matrix elements as [26]
in eq. (4) is calculated in terms of the isospin-reduced matrix elements as [26]
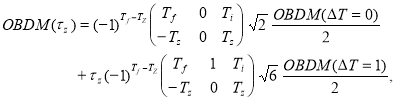 (5)
(5)
where 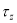 is the isospin operator of the single particle.
is the isospin operator of the single particle.
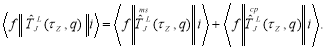 (6)
(6)
The model space matrix element, in eq. (6), is given by
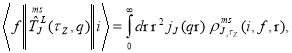 (7)
(7)
where 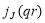 is the spherical Bessel function and
is the spherical Bessel function and 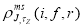 is the model space transition charge density, expressed as the sum of the product of the
is the model space transition charge density, expressed as the sum of the product of the 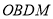 times the single particle matrix elements, given by [26].
times the single particle matrix elements, given by [26].
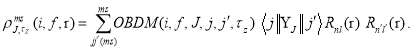 (8)
(8)
Here, 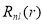 is the radial part of the harmonic oscillator wave function and
is the radial part of the harmonic oscillator wave function and 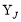 is the spherical harmonic wave function.
is the spherical harmonic wave function.
The core-polarization matrix element, in eq. (6), is given by
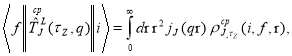 (9)
(9)
where 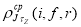 is the core-polarization transition charge density which depends on the model used for core polarization. To take the core-polarization effects into consideration, the model space transition charge density is added to the core-polarization transition charge density that describes the collective modes of nuclei. The total transition charge density becomes
is the core-polarization transition charge density which depends on the model used for core polarization. To take the core-polarization effects into consideration, the model space transition charge density is added to the core-polarization transition charge density that describes the collective modes of nuclei. The total transition charge density becomes
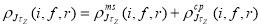 (10)
(10)
According to the collective modes of nuclei, the core polarization transition charge density is assumed to have the form of Tassie shape [27]
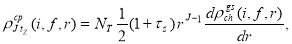 (11)
(11)
where 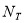 is the proportionality constant given by [14]
is the proportionality constant given by [14]
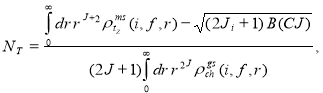 (12)
(12)
which can be determind by adusting the reduced transition probability 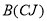 to the experimental value, and
to the experimental value, and 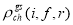 is the ground state charge density distribution of considered nuclei.
is the ground state charge density distribution of considered nuclei.
For  the ground state charge densities
the ground state charge densities 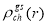 of closed shell nuclei may be related to the ground state point nucleon densities
of closed shell nuclei may be related to the ground state point nucleon densities 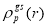 by [28, 29]
by [28, 29]
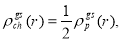 (13)
(13)
in unit of electronic charge per unit volume (e.fm-3).
An expression of the correlated density 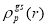 (where the effect of the SRC’s is included), consists of one- and two-body terms, is given by [13]
(where the effect of the SRC’s is included), consists of one- and two-body terms, is given by [13]
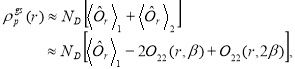 (14)
(14)
where 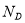 is the normalization factor and
is the normalization factor and 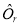 is the one body density operator given by
is the one body density operator given by
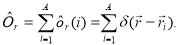 (15)
(15)
The correlated density 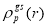 of eq. (14), which is truncated at the two-body term and originated by the factor cluster expansion of Clark and co-workers [10-12], depends on the correlation parameter
of eq. (14), which is truncated at the two-body term and originated by the factor cluster expansion of Clark and co-workers [10-12], depends on the correlation parameter 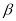 through the Jastrow-type correlation
through the Jastrow-type correlation
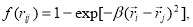 (16)
(16)
where 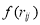 is a state-independent correlation function, which has the following properties:
is a state-independent correlation function, which has the following properties: 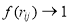 for large values of
for large values of 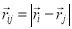 and
and 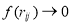 for
for 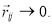 It is so clear that the effect of SRC’s, inserted by the function
It is so clear that the effect of SRC’s, inserted by the function 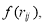 becomes large for small values of SRC parameter
becomes large for small values of SRC parameter 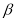 and vice versa.
and vice versa.
The one-body term, in eq. (14), is well known and given by
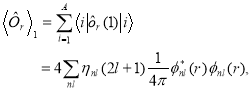 (17)
(17)
where 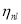 is the occupation probability of the state
is the occupation probability of the state 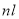 and
and 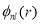 is the radial part of the single particle harmonic oscillator wave function.
is the radial part of the single particle harmonic oscillator wave function.
The two-body term, in eq. (14), is given by [13]
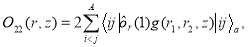
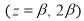 (18)
(18)
where
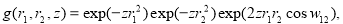 (19)
(19)
The form of the two-body term 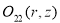 is then originated by expanding the factor
is then originated by expanding the factor 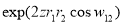 in the spherical harmonics and expressed as [13]
in the spherical harmonics and expressed as [13]
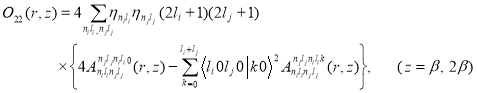 (20)
(20)
where
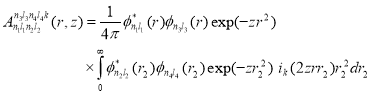 (21)
(21)
and  is the Clebsch-Gordan coefficients.
is the Clebsch-Gordan coefficients.
It is important to point out that the expressions of eqs. (17) And (20) are originated for closed shell nuclei with  where the occupation probability
where the occupation probability  is 0 or 1. To extend the calculations for isotopes of closed shell nuclei, the correlated charge densities of these isotopes are characterized by the same expressions of eqs. (17) and (20) (this is because all isotopic chain nuclei have the same atomic number
is 0 or 1. To extend the calculations for isotopes of closed shell nuclei, the correlated charge densities of these isotopes are characterized by the same expressions of eqs. (17) and (20) (this is because all isotopic chain nuclei have the same atomic number 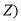 but this time different values for the parameters
but this time different values for the parameters 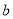 and
and 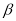 are utilized.
are utilized.
The mean square charge radii of nuclei are defined by
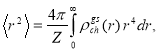 (22)
(22)
where the normalzation of the charge density distribution 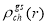 is given by
is given by
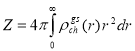 (23)
(23)
3-Results and discussion
The ground state CDD is calculated by eq.(13) together with eqs. (14), (17) and (20). The calculated CDD without (with) the effect of the SRC [i.e., when the correlation parameter 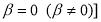 is obtained by adjusting only the parameter
is obtained by adjusting only the parameter  (the two parameters
(the two parameters 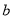 and
and 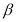 ) so as to reproduce the experimental root mean square (rms) charge radii of nuclei under study. The elastic electron scattering charge form factors which is simply the Fourier transform of the ground state CDD.
) so as to reproduce the experimental root mean square (rms) charge radii of nuclei under study. The elastic electron scattering charge form factors which is simply the Fourier transform of the ground state CDD.
In Fig. 1, we compare the calculated CDD [Fig. 1(a)] and elastic charge form factors [Fig. 1(b)] of 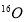 with those of experimental data (the open circles). In Fig. 1, we compare the calculated CDD [Fig. 1 (a)] and elastic charge form factors [Fig. 1 (b)] of
with those of experimental data (the open circles). In Fig. 1, we compare the calculated CDD [Fig. 1 (a)] and elastic charge form factors [Fig. 1 (b)] of 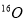 with those of experimental data (the open circles). The dashed curves are the calculated results without the inclusion of the effect of the SRC obtained with
with those of experimental data (the open circles). The dashed curves are the calculated results without the inclusion of the effect of the SRC obtained with 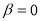 and
and 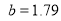 fm. The solid curves are the calculated results with including the effect of the SRC obtained with
fm. The solid curves are the calculated results with including the effect of the SRC obtained with 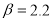 fm-2 and
fm-2 and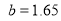 fm. It is important to point out that the parameters
fm. It is important to point out that the parameters 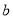 and
and 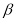 employed in the calculations of the dashed and solid curves are chosen so as to reproduce the experimental rms charge radius of
employed in the calculations of the dashed and solid curves are chosen so as to reproduce the experimental rms charge radius of 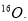 Fig. 1 (a) illustrates that the calculated CDD of the dashed curve (without the effect of the SRC) is in such a good agreement with that of the experimental data, and the solid curve (with the effect of the SRC) is not in such a good agreement with that of the experimental data, especially in the central region (
Fig. 1 (a) illustrates that the calculated CDD of the dashed curve (without the effect of the SRC) is in such a good agreement with that of the experimental data, and the solid curve (with the effect of the SRC) is not in such a good agreement with that of the experimental data, especially in the central region (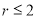 fm) of the distributions. The inclusion of SRC has the feature of reducing the central region of the distribution as seen in the solid curve of this figure. Inspection to the Fig. 1 (b) gives an indication that the solid curve is better describing the experimental data than that of the dashed curve, particularly in the region of momentum transfer
fm) of the distributions. The inclusion of SRC has the feature of reducing the central region of the distribution as seen in the solid curve of this figure. Inspection to the Fig. 1 (b) gives an indication that the solid curve is better describing the experimental data than that of the dashed curve, particularly in the region of momentum transfer 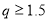 fm-1. The rms charge radius calculated with the above values of
fm-1. The rms charge radius calculated with the above values of 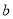 and
and 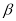 is 2.621 fm, which is less than the experimental value by 0.097fm, which corresponds to a decrease of nearly 3.6 % of the experimental value.
is 2.621 fm, which is less than the experimental value by 0.097fm, which corresponds to a decrease of nearly 3.6 % of the experimental value.
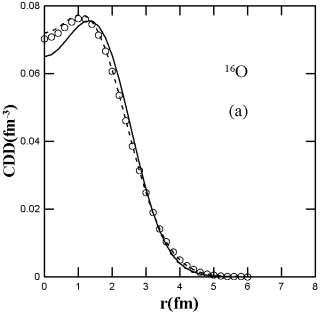
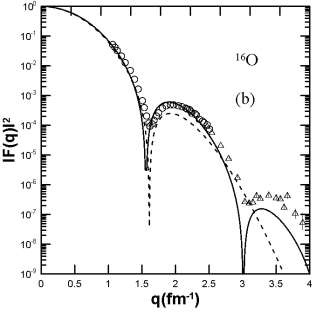
Fig. 1. The calculated CDD and elastic charge form factors are compared with those of experimental data. The dashed curve corresponds to the values for the parameters 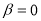 and
and 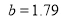 fm, the solid curve corresponds to the values for the parameters
fm, the solid curve corresponds to the values for the parameters 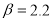 fm-2 and
fm-2 and 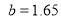 fm while the open circles and the triangles in Figs. 1 (a) and 1 (b) are the experimental data taken from [30] and [31], respectively.
fm while the open circles and the triangles in Figs. 1 (a) and 1 (b) are the experimental data taken from [30] and [31], respectively.
The effect of the SRC on the inelastic Coulomb form factors is studied for the two excited 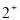 states (6.92 and 11.52 MeV) in
states (6.92 and 11.52 MeV) in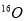 . Core polarization effects are taken into consideration by means of the Tassie model [eq. (11)], where this model depends on the ground state charge density distribution. The proportionality constant
. Core polarization effects are taken into consideration by means of the Tassie model [eq. (11)], where this model depends on the ground state charge density distribution. The proportionality constant 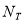 [eq. (12)] is estimated by adjusting the reduced transition probability
[eq. (12)] is estimated by adjusting the reduced transition probability 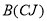 to the experimental value. The effect of the SRC is incorporated into the ground state charge density distribution through the Jastrow type correlation function [12]. The single particle harmonic oscillator wave function is employed with an oscillator size parameter
to the experimental value. The effect of the SRC is incorporated into the ground state charge density distribution through the Jastrow type correlation function [12]. The single particle harmonic oscillator wave function is employed with an oscillator size parameter 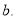
The charge density distribution calculated without the effect of the SRC depends only on one free parameter (namely the parameter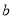 ), where
), where 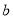 is chosen in such away so as to reproduce the experimental rms charge radii of considered nuclei. The charge density distribution calculated with the effect of the SRC depends on two free parameters (namely the harmonic oscillator size parameter
is chosen in such away so as to reproduce the experimental rms charge radii of considered nuclei. The charge density distribution calculated with the effect of the SRC depends on two free parameters (namely the harmonic oscillator size parameter 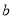 and the correlation parameter
and the correlation parameter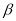 ), where these parameters are adjusted for each excited state separately so as to reproduce the experimental rms charge radii of considered nuclei.
), where these parameters are adjusted for each excited state separately so as to reproduce the experimental rms charge radii of considered nuclei.
Two different models are employed for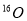 . In the first model (model A),
. In the first model (model A), 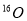 is considered as a closed shell nucleus. In this model, the proton occupation probabilities in
is considered as a closed shell nucleus. In this model, the proton occupation probabilities in 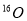 are assumed to be
are assumed to be 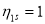 and
and 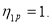 Here, the model space in
Here, the model space in 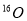 does not contribute to the transition charge density [i.e.
does not contribute to the transition charge density [i.e. 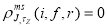 ], because there are no protons outside the closed shell nucleus
], because there are no protons outside the closed shell nucleus 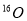 . Accordingly, the Coloumb form factors of
. Accordingly, the Coloumb form factors of 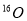 come entirely from the core polarization transition charge density. In the second model (model B), the nucleus of
come entirely from the core polarization transition charge density. In the second model (model B), the nucleus of 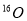 is assumed as a core of
is assumed as a core of 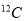 with 2 protons and 2 neutrons move in
with 2 protons and 2 neutrons move in 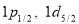 and
and 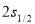 model space. In this model, the proton occupation probabilities in
model space. In this model, the proton occupation probabilities in 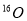 are assumed to be
are assumed to be 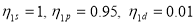 and
and 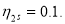 Here, the total transition charge density [eq. (10)] comes from both the model space and core polarization transition charge densities. The OBDM elements of
Here, the total transition charge density [eq. (10)] comes from both the model space and core polarization transition charge densities. The OBDM elements of 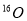 are generated, via the shell model code OXBASH [32], using the REWIL [33] as a realistic effective interaction in the isospin formalism for 4 particles move in the
are generated, via the shell model code OXBASH [32], using the REWIL [33] as a realistic effective interaction in the isospin formalism for 4 particles move in the 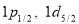 and
and 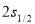 model space with a
model space with a 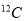 core.
core.
In Table 1, the experimental excitation energies 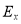 (MeV), experimental reduced transition probabilities
(MeV), experimental reduced transition probabilities 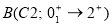 (
(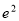 fm
fm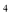 ) and the chosen values for the parameters
) and the chosen values for the parameters 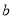 and
and 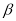 for each excited state (used in the calculations of model A and B) in
for each excited state (used in the calculations of model A and B) in 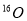 and
and 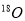 are displayed. The root mean square (rms) charge radius calculated in both models with the effect of SRC is also displayed in this table and compared with that of experimental result. It is evident from this table that the values of the parameter
are displayed. The root mean square (rms) charge radius calculated in both models with the effect of SRC is also displayed in this table and compared with that of experimental result. It is evident from this table that the values of the parameter 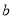 employed for calculations with the effect of SRC are smaller than that of without SRC (
employed for calculations with the effect of SRC are smaller than that of without SRC (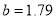 fm) . This is attributed to the fact that the introduction of SRC leads to enlarge the relative distance of the nucleons (i.e., the size of the nucleus) whereas the parameter
fm) . This is attributed to the fact that the introduction of SRC leads to enlarge the relative distance of the nucleons (i.e., the size of the nucleus) whereas the parameter 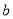 (which is proportional to the radius of the nucleus) should become smaller so as to reproduce the experimental rms charge radius of the considered nuclei.
(which is proportional to the radius of the nucleus) should become smaller so as to reproduce the experimental rms charge radius of the considered nuclei.
Inelastic Coloumb form factors for different transitions in 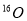 are displayed in Figs. 1 and 2. The calculated inelastic form factors obtained with model A are shown in the upper panel [Figs. 1(a)-2(a)] of the above figures whereas those obtained with model B are shown in the lower panel [Figs. 1(b)- 2(b)] of the above figures. It is obvious that all transitions considered in
are displayed in Figs. 1 and 2. The calculated inelastic form factors obtained with model A are shown in the upper panel [Figs. 1(a)-2(a)] of the above figures whereas those obtained with model B are shown in the lower panel [Figs. 1(b)- 2(b)] of the above figures. It is obvious that all transitions considered in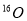 , presented in the above figures, are of an isoscalar character. Besides, the parity of them does not change. Here, the calculated inelastic form factors are plotted versus the momentum transfer
, presented in the above figures, are of an isoscalar character. Besides, the parity of them does not change. Here, the calculated inelastic form factors are plotted versus the momentum transfer 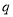 and compared with those of experimental data. The dashed and solid curves are the calculated inelastic Coloumb form factors without and with the inclusion of the effect of the SRC, respectively. The open symbols are those of experimental data taken from [34, 35].
and compared with those of experimental data. The dashed and solid curves are the calculated inelastic Coloumb form factors without and with the inclusion of the effect of the SRC, respectively. The open symbols are those of experimental data taken from [34, 35].
Table1. The experimental excitation energies and reduced transition probabilities, the chosen values for 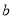 and
and 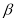 as well as the rms charge radius calculated with the effect of the SRC of 16O.
as well as the rms charge radius calculated with the effect of the SRC of 16O.
|
(fm) |
Model B |
Model A |
|
(MeV) |
State |
||||
|
|
(fm-2) |
(fm) |
|
(fm-2) |
(fm) |
||||
|
|
2.704 | ||||||||
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal
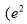 fm2L)
fm2L)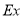
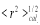 (fm)
(fm)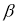
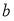
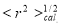 (fm)
(fm)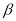
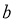
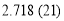 [30]
[30]


