Discharge of Water through a Spherical Orifice

There are multiple factors that affect the discharge of water through a spherical orifice. These can include the height of water above the incision, the cross sectional area of the hole and the shape of the hole that the fluid is flowing through [New Century Senior Physics 2004]. But first of all, what is fluid?    

Fluids are defined as any substance that cannot sustain any tangential or shearing force while maintaining its form at rest, basically any substance in the form of a gas or liquid [Britannica 2017]. They generally have no fixed shape and when exposed to stress, the fluid will experience a continuous change [Britannica 2017].

Flow is a universal property for all fluids [Britannica 2017]. For liquids in particular, the flow is influenced by the acceleration due to gravity. If the fluid is non-viscous and incompressible, while the flow of the fluid is steady, then this flow can be seen from an energy perspective [Fluid Mechanics and Bernoulli's Principle 1999]. In pipes, there are two factors to allow a fluid to flow, the first method is to tilt the pipe so the fluid gains Gravitational Potential Energy [Fluid Mechanics and Bernoulli's equation 1999]. This is defined as the stored energy that liquids or solids with mass possess that is dependent on the acceleration due to gravity and the respective height the object or substance above the ground [Hyperphysics 2017]. When the pipe has been tilted enough, the flow will be 'downhill', this moment is where the accumulated gravitational potential energy is transferred to kinetic energy, the energy of motion, hence creating the flow of a fluid [Fluid Mechanics and Bernoulli's Principle 1999]. The law of conservation of energy states that 'for any physical or chemical change, energy cannot be created nor destroyed', this describes this procedure of the energy transfer previously mentioned [Madden et al. 2004]. {FLOW}

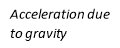
The second method to make a fluid flow is to increase the pressure at one end of the pipe so it is larger than the pressure accumulated on the other end. This in turn creates a pressure difference which acts as a net force, accelerating the fluid through the pipe which is known as flow [Fluid Dynamics and Bernoulli's Principle 1999].

Jets are a common form of fluid flow. They are defined as a fluid discharged forcefully through a narrow opening or orifice, resulting in a stream like motion [Meriam Webster 2017]. One of the main components of the jet is its velocity, this is affected by multiple factors including the hole's size and shape, the fluid's pressure and viscosity, even the medium which it passes through can, inhibit the jet's potential velocity. If the composition of the jet's fluid is somewhat identical with a stationary medium surrounding the flow, the jet can be classed a submerged jet [Farlex Inc 2017]. Examples of this flow are the air currents through a still atmosphere, this is because the fluid is air and the surrounding media is also air [Farlex Inc 2017]. There are many other forms of jets including free jets which are the opposite from submerged, they are where the jet passes through unbounded mediums. Semi-contained jets occur when the jet passes along a flat surface while confined jets exist in mediums bounded by solid surfaces, for example a pipe with a diameter larger than that of the inlet [Farlex Inc. 2017]. {Jets, discharge, vena contracta?}

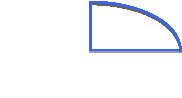
When fluid jets are in motion, their cross sectional area is quite often subject to contracting. The site of this contraction is known as the natural phenomenon of vena contracta, which can be defined as any of the locations in a jet of fluid emerging from and orifice where the flow's cross sectional area is at its minimum [Dicionary.com, LLC 2016]. Vena contracta usually occurs as a result of the fluid's streamlines converging as they approach an orifice [Calvert J.B. 2003]. Generally, this leads to the cross sectional area of the jet decreasing slightly until the pressure in the cross-section has been equalized, it is also at this point where the jet experiences its maximum velocity in its flow [Calvert J.B. 2003]. Beyond the site of vena contracta, the jet's streams start to diverge as a result of friction and drag caused by the jet flowing through another fluid, in this case, the air surrounding the flow [Calvert J.B. 2003]. The cross-sectional area will increase while the jet decelerates from the surrounding fluid as a result which is why the jet can be seen transforming from a constant flow to small droplets. Jet's are held together by surface tension which is why they generally do not continue to be a perfect flow, this tension has a stronger effect the smaller the diameter of the jet [J.B. Calvert 2003]. This is why decreasing the size of the orifice will lead to an increase in the displacement of the jet from the container because by decreasing the cross section, the jet will accumulate more velocity at vena contracta.

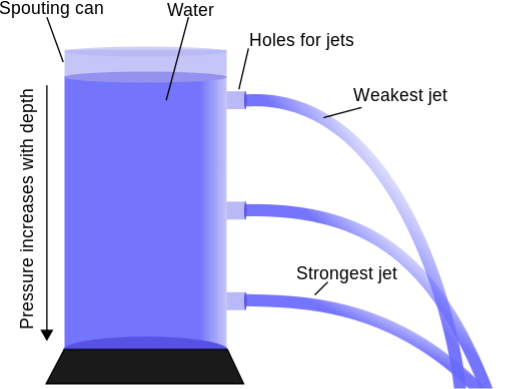
Pressure is another factor that affects the displacement of the jet from the orifice. If the pressure accumulated inside the container is substantially high, the fluid tends to compress in a closed container [Spence Regan 2007]. However, if the fluid is incompressible like water, an increase in pressure will generally lead the fluid molecules to basically 'push' up against the walls of the container as it attempts to decompress back to the normal atmospheric pressure surrounding the container [Spence Regan 2007]. Because of this, when a leak has been sprung in a container consisting of a pressurized fluid, the fluid will be inclined to escape, and with more pressure, the faster the fluids discharging velocity will be [Khan Academy 2017]. Naturally, especially when dealing with water as a fluid, pressure is most commonly affected by and directly proportional to the height of the water's (fluid's) surface above the specific measured location, or the depth of the location from that surface [Madden et al. 2004]. The reason for this is because the height of the fluid administers a mass over that specific location, which then, assuming that the fluid analysed is influenced by the acceleration due to gravity, a force will be produced as stated in the equation below [Madden et al. 2004].

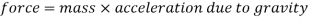
or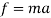

[Madden et al. 2004]

This accumulated force will result in Pressure through the equation

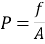
Where:

P= Pressure (Pa)

f=force (N)

A=Area (m²)

[Madden et al. 2004]

However in fluid mechanics, another more accurate equation is required, this is known as Bernoulli's equation which relates to Bernoulli's Principle. This principle is based on the law of conservation of energy and states that a fluid's pressure decreases when it is subjected to increased velocities, vice versa [Madden et al. 2004]. The pressure, velocity or heights of surfaces above the hole in most fluids are related to the same parameters at a second point through Bernoulli's equation as stated below [Fluid Dynamics and Bernoulli's equation 1999].

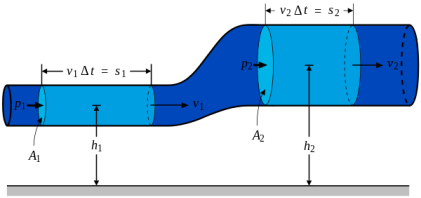
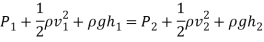
Where:

P=Pressure (Pa)

ρ=Density (kgm^-3)

v=Velocity of Fluid (ms^-1)

g=Acceleration due to gravity (ms^-2)

h=Height (m)

[Madden et al. 2004]

The pressure of a fluid at depth can be given through a derivative of Bernoulli's equation.

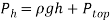
Where:

P_h=the pressure at depth (Pa)

ρ=density of fluid (kgm^-3)

g=acceleration due to gravity (9.81ms^-2)

h=the height of the fluid's surface, in this case the water, above the specific location where Pressure at depth is measured.

P_top = the pressure at the fluid's surface (Pa)

[Madden et al. 2004].

This equation can be used to find the pressure at certain points like at the same level as the orifice inside the bottle [Madden et al. 2004]. For this experiment however, the pressure will be measured and calculated at the same level as the orifice and since the pressure at the fluid's surface can also be considered as the air temperature inside the room this will also be used in the equation.

For eg, If the water's density, the acceleration due to gravity and the air pressure were kept at constant while the height of the surface above a certain location was increased, then the Pressure at that location should also increase like so [Madden et al. 2004].

If ρ=1000kgm^-3, P_top=94500Pa and g=9.81ms^-2

When h= 10m

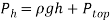
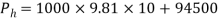
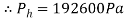
[Madden et al. 2004]

This is important in many applications like dams, towns and especially high rise buildings. Water will need to be mechanically pushed up to the top of a building so people at the top floors can have sufficient water to have a shower [Madden et al. 2004]. It is also because of this understanding of fluid mechanics that hilly cities often build water towers or reservoirs at the top of hills or mountains to help accumulate this needed pressure to effectively distribute water to the population [Madden et al. 2004].

Pressure can directly affect the exit velocity of the fluid being discharged as it flows out through an opening in any form of container or reservoir. This is known as the velocity of efflux and is determined through many similar formulae. The most common is derived from Torricelli's theorem which is about the relationship between the height of the fluid above the orifice, and the exit velocity of the fluid projected from a sharp edged orifice [Boundless 2016]. The law also states that the speed (velocity) of a liquid flowing under the influence of gravity out of an orifice in a reservoir is directly proportional to the square root of the vertical distance between the surface of the liquid and orifice and the square root twice the acceleration due to gravity [Britannica 2017]. The equation that relates to this theorem is stated below.

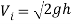
Where:

V_i= Velocity of Efflux (ms^-1)

g= Acceleration due to gravity

h= Height of the fluid's surface above the orifice

This velocity is a result from a transfer of potential energy to kinetic energy [Boundless 2016]{Torricelli's Law and height/Displacement}

Other deviations of this equation can be used to factor in for orifice and container sizes like displayed below.

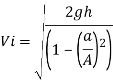
Where:

A= Area of Container (m²)

a= Area of Orifice (m²)

[CalcTown 2017]

In this case the areas can be calculated using the standard area formula for a circle. According to calculations using this formula however, velocities are not effected significantly from changing the container's area or even the orifice's area. But the area of the orifice seems to affect this velocity more adversely than the area of the bottle which is why changing the area of the bottle will not be tested in the experiment [CalcTown 2017].

Orifices also come in many different shapes or categories. The most common of these is the sharp edged orifice which is a simple hole [lmnoeng 2016]. Other common orifices include smooth edged, short tube and borda which appears to be a short tube on the interior of the container. Each different hole affects the velocities and displacements of the jet as the jet is subjected to either more or less friction and drag through each different hole type [lmnoeng 2016]. This results in many different coefficients of discharge and velocity which can then be inserted into equations. The orifice types are displayed below.

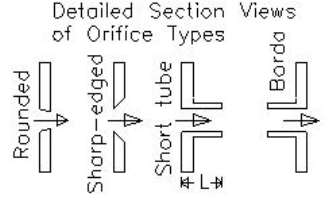
According to multiple experiments the average coefficients of velocity for each orifice have been determined. The orifices that will be used for this experiment are the Sharp edged, Short tube and Borda because the Rounded orifice is too hard to replicate using the resrouces on hand. The sharp edged orifice has an average velocity coefficient of 0.98 as well as the borda hole. The short tube has a velocity coefficient of 0.8 [LMNOeng 2016].

The equation that can implement this coefficient is a derivative of Toricelli's

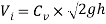
The viscosity of the fluid can also affect a fluids flow displacement out of an orifice. Viscosity is defined as the resistance of flow and is the result of the interaction and friction between different molecules in a fluid, at a molecular level [rheosense 2017]. A substance that has high viscosity has high friction and flows through an orifice slowly, this in turn means that it would not be displaced very far from the hole, an example of this is honey [rheosense 2017]. Viscosity can be decreased with an increase in temperature [Viscopedia 2017]. Water however is said to have a low viscosity, so this temperature change theoretically should not affect its discharge to much which is why temperature will not be a variable that will be tested [Viscopedia 2017].

To determine each of the horizontal displacements that the jet will theoretically travel, the cross sectional area of the 1.25L soft drink bottle (A) needs to be calculated first through the simple area equation for a circle. This will be used universally to calculate the Velocity of Efflux.

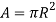
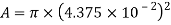
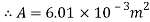
[Simson & Rowland 2010]

Since this first experiment is testing the displacement of water through a diameter change, the cross sectional area of the orifice (a) needs to be calculated next. The height of the surface as a variable is kept at a constant 0.012m, while for this example, the diameter of the orifice is 3.18mm.

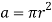
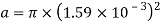
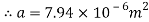
[Simpson & Rowland 2010]

Then the pressure at depth can also be calculated next from Bernoulli's standard fluid equation and for this first experiment, the pressure determined will be the same for each hole size being tested. Assuming that the pressure at the surface of the fluid is 94500Pa, the density of water is 1000kgm^-3 and the height of the surface above the orifice is 0.12m, the pressure of the fluid at the same level as the orifice should be given below.

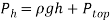
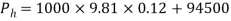
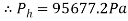
[Madden et al. 2004]

A deviation of Toricelli's equation can then be used to determine the velocity of efflux with in the jet. The value calculated can be used to determine the theoretical displacement of the jet.

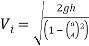
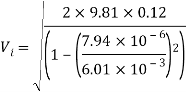
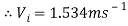
[CalcTown 2015]

And now the maximum displacement the water is expected to discharge can be found using another deviation of Torricelli's equation that has been rearranged slightly to fit requirements. Assume that the orifice height from the bottle is 0.19m above the location where horizontal displacement is measured (ruler).

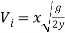
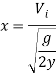
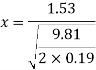
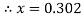m

[Calvert, J.B. 2003]

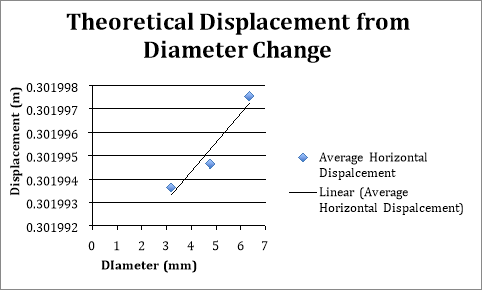
Therefore based off theses assumptions and calculations, theoretically, when the jet starts flowing from a surface height of 0.12m and an orifice diameter of 3.18mm, the fluid should be displaced about 0.302m from the orifice. The theoretical displacements of the water are displayed in the table and graph below.

These displacements are the same, however by increasing the hole size, the displacement does increase however by not a large amount as displayed in the graph below.

Due to background research above, the theoretical displacements of the water in experiment 2 can be determined from each of the heights that will be used. Beginning at the surface height of 0.04m, theoretical displacements can be determined from the following calculations assuming that the jet is not affected by air resistance and the pressure at the surface of the fluid is 94500Pa.

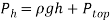
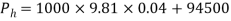
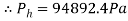
[Madden et al. 2004]

So the pressure at the hole should be 94892.4Pa. The velocity of the jet can then be calculated using the areas calculated before and the same deviation of Torricelli's law.

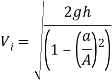
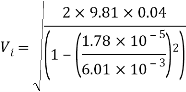
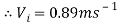
[CalcTown 2015]

Using this value calculated, the horizontal displacement can be determined using the equation from experiment 1, still assuming that the height of the orifice above the location of measuring is 0.19m.

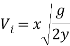
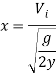
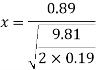
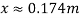
[Calvert, J.B 2003]

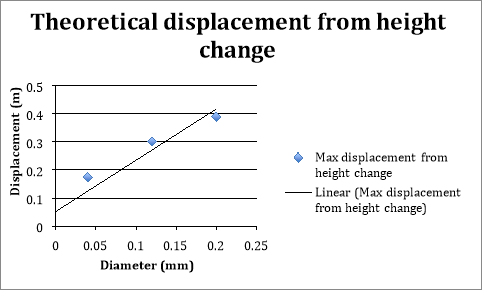
Therefore the expected horizontal displacement when the height of the surface is 0.04m is 0.174m. The other results calculated using these formulae are displayed in the table and graph below.

A new set of equations will need to be used to determine the velocity of efflux, seeing as the formulae previously used only factors in surface heights, orifice and bottle sizes. This formula will need to utilize the coefficient of velocity for each hole shape as this coefficient supposedly changes with a change in hole type. Beginning with the first hole, borda (interior tube), we will assume that the height will be 0.12m, air resistance does not affect discharge and the coefficient of velocity will be the same as the average researched for this hole, 0.98. A deviation of Torricelli's equation will be used to incorporate this coefficient into calculating the velocity of efflux but first the pressure inside the bottle will need to be calculated.

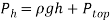
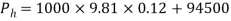
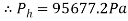
[Madden et al. 2004]

Now the Velocity of efflux will be calculated as previously mentioned, also assuming the same factors previously mentioned.

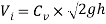
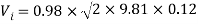
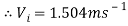
[LMNO Engineering, Research, and Software, Ltd 2015]

Using this velocity, the expected horizontal displacement of the jet can then be calculated using the same equation and method used in previous tests.

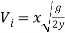
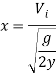
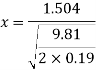
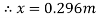
[Calvert J.B. 2003]

Therefore the expected displacement the jet should be displaced using a Borda orifice is 0.296m, that is if all assumptions made come into effect in the experiment. All results calculated using this same format and assumptions are displayed in the table and graph below. The other orifice use different coefficients to be calculated, it is assumed that for the Sharp edged orifice, the velocity coefficient will be 0.98 like Borda, and for the short tube, the coefficient is 0.80.