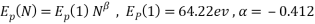Argon Cluster and Graphene Collision Simulation Experiment

Formation of Nanopore in a Suspended Graphene Sheet with Argon Cluster Bombardment: A Molecular Dynamics Simulation study

Abstract: Formation of a nanopore in a suspended graphene sheet using an argon gas beam was simulated using molecular dynamics (MD) method. The Lennard-Jones (LJ) two-body potential and Tersoff–Brenner empirical potential energy function are applied in the MD simulations for different interactions between particles. The simulation results demonstrated that the incident energy and cluster size played a crucial role in the collisions. Simulation results for the Ar55 –graphene collisions show that the Ar55 cluster bounces back when the incident energy is less than 11ev/atom, the argon cluster penetrates when the incident energy is greater than 14 ev/atom. The two threshold incident energies, i.e. threshold incident energy of defect formation in graphene and threshold energy of penetration argon cluster were observed in the simulation. The threshold energies were found to have relatively weak negative power law dependence on the cluster size. The number of sputtered carbon atoms is obtained as a function of the kinetic energy of the cluster.

Keywords: Nanopore, Suspended graphene sheet, Argon cluster, Molecular dynamics simulation

1. Introduction

The carbon atoms in graphene condense in a honeycomb lattice due to sp2-hybridized carbon bond in two dimensions [1]. It has unique mechanical [2], thermal [3-4], electronic [5], optical [6], and transport properties [7], which leads to its huge potential applications in nanoelectronic and energy science [8]. One of the key obstacles of pristine graphene in nanoelectronics is the absence of band gap [9-10]. Theoretical studies have shown that chemical doping of graphene with foreign atoms can modulate the electronic band structure of graphene and lead to the metal to semiconductor transition and break the polarized transport degeneracy [11-12]. Also, computational studies have demonstrated that some vacancies of carbon atoms within the graphene plane could induce a band-gap opening and Fermi level shifting [13-14]. Graphene nanopores can have potential applications in various technologies, such as DNA sequencing, gas separation, and single-molecule analysis [15-16]. Generating sub-nanometer pores with precisely-controlled sizes is the key difficulty in the design of a graphene nanopore device. Several method have been employed to punch nanopores in graphene sheets, including electron beam from a transmission electron microscope (TEM) and heavy ion irradiation.

Using electron beam technique, Fischbein et al.[17] drilled nanopores with the width of several nanometers and demonstrated that porous graphene is very stable; but, this method cannot be widely used because of its low efficiency and high cost. Russo et al. [18] used energetic ion exposure technique to create nanopores with radius as small as 3Å. S. Zhao et al. [19] indicated that energetic cluster irradiation was more effective in generating nanopores in graphene, because their much larger kinetic energy could be transferred to the target atoms. Recent experimental works have further confirmed that cluster irradiation is a feasible and promising way in the generation of nanopores [20]. Numerical simulations have demonstrated that, by choosing a suitable cluster species and controlling its energy, a nanopores of desired sizes and qualities can be fabricated in a graphene sheet [19].

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

A useful tool for studying the influence of different conditions of interactions between cluster and graphene on the formation of nanopore is numerical simulations utilizing molecular dynamics (MD) [21]. The results may be useful in explaining experimental results and predicting optimal conditions for desirable graphene nanopores.

In this paper, MD simulations were performed for the collisions between an argon cluster and graphene. The phenomena of argon cluster–graphene collisions and mechanism of the atomic nanopore formation in graphene were investigated. Effects of cluster size on the threshold incident energy of defect formation in graphene were also discussed.

2. Molecular Dynamics Method

MD simulations were performed for the collisions between an argon cluster and graphene. For present simulations we used an effective code LAMMPS stands for Large-scale Atomic/Molecular Massively Parallel Simulator, written by Sandia National Laboratories [22]. Length (along the X axis) of the graphene layer was 11 nm, its width (along the Y axis) was 10 nm, and each layer contained 3936 atoms. Periodic boundary conditions were applied to both lateral directions. In the simulation, the Tersoff–Brenner empirical potential energy function (PEF) was utilized to simulate the energy of covalent bonding between carbon atoms in the structure of graphene layer [23-24]. The initial configuration was fully relaxed before the collision simulations and the target temperature was maintained at 300 K. During the collision phase, a thermostat was applied to the borders of graphene. The Ar nanocluster was arranged by cutting a sphere from FCC bulk crystals, which had no initial thermal motion. The Ar cluster was initially located above the center of graphene at a sufficiently large distance so that there would be no interaction between the Ar and graphene atoms. Then, a negative translational velocity component, Vz, was assumed for each atom of the clusters. Incident angle of the argon cluster to the graphene normal was zero. Lennard-Jones (LJ) two-body potential was employed to simulate the interactions of Ar–Ar and Ar–C atoms. The form of LJ potentials was:

In the LJ potential, is the distance at which the potential is zero and is the depth of the potential well. Note that the constants were obtained from the mixing rules given by σij = (σi+σj)/2 and Ԑij = (ԐiԐj)1/2. The parameters for Ԑ and σ used in the present simulation are shown in Table 1[25]. Position of the atom was updated by the velocity Verlet algorithm with a time step of less than t = 0.5 fs. To reduce the calculation time, a cut-off length was introduced. The Van der Waals interaction of Ar-Ar and Ar-C atoms with the distance of 11A or above was neglected.

3. Result

Studying the effect of incident energy in ranging 1–120 ev/atom was chosen to demonstrate two distinctive phenomena: (i) Argon atoms were just reflected, and (ii) some argon atoms penetrated through graphene. Fig. 1 demonstrates the probabilities of reflection and penetration of the Ar55 cluster.

Fig. 2 shows the snapshots of the deformation of the graphene sheet due to the collision with an Ar55 cluster in the case of the incident energy of less than 11ev. During the collision, graphene was bended in the circular region around the collision point and the transverse deflection wave was observed. After the collision, argon cluster was bursted into fragments.

Fig. 3 shows the final atomic configurations resulted from the incidence of Ar55 cluster with the energy of 10 and 11 ev/atom. There were two possibilities for the structure of the graphene sheet after the collision: (i) the graphene was rippled after the collision and no damaged region was formed, this was observed in case of the incident energy of less than 11ev (Fig. 3(a)), and (ii) the collision caused defect in graphene (Fig. 3(b)).

Fig. 4 shows that there were two possibilities for the structure of the graphene sheet after collision with an Ar55 cluster in the case of the incident energy of greater than 11 ev/atom: (i) the argon cluster penetrated into the graphene sheet without the sputtered carbon atoms (Fig. 4(a)), and (ii) the argon cluster penetrated into the graphene sheet with the sputtered carbon atoms (Fig. 4(b)). When the incident energy of argon cluster was 11ev/atom, atomic-scale defects such as Stone−Wales defect were formed in the graphene sheet (Fig. 3(b)). With the increase of the incident energy, these atomic defects began to get connected and finally a nanopore with carbon chains on the pore edge was created in graphene. The atomic carbon chains with unsaturated bonds thus provided the method for chemical functionalization of graphene nanopores in order to improve their separation ability and detection. For example, oxidation of packed multilayered graphene sheets was significantly permeable to water and impermeable to He, N2, Ar, and H2 [26].

Accordingly, it was necessary to introduce the concept of threshold incident energy of defect formation (Ed) in graphene and threshold energy (Ep) of penetration argon cluster in graphene. Fig. 5 shows the size dependence of each threshold incident energy. Thus, both Ed and Ep were supposed to be written in simple power-law equations:

Fig. 6 shows the final atomic configurations resulted from the incidence of Ar55 cluster with the energy of 14 , 15 ev/atom. By further increasing energy, the carbon chains became short and the pore edge became smooth

we calculated the number of sputtered carbon atoms as a function of total incident energy, because the number of the sputtered carbon atoms was in correspondence to the area of nanopore in graphene. Fig. 7 shows the number of sputtered carbon atoms as a function of total cluster energy in the case of Ar19 and Ar55 cluster collision. For both cases, as the total energy increased, the number of sputtered carbon atoms increased. This result was in agreement with the previous study [27] .The number of sputtered carbon atoms can be approximated by a constant value for incident energy larger than 10 Kev. The cluster collision with large size led to higher the number of sputtered carbon atoms when all clusters had the same total cluster energy.

4. Conclusions

The phenomena of argon cluster–graphene collisions and mechanism of the atomic nanopore formation in suspended graphene sheet were investigated using molecular dynamics method. Summary of the obtained results is as follows:

• Threshold incident energy which caused defect formation (Ed) in graphene and penetration (Ep) into argon cluster were introduced.
• Simulation results for the argon cluster–graphene collisions showed that the argon cluster bounced back when the incident energy was less than Ed and broke when the incident energy was greater than Ep.
• Suspended carbon chains could be formed at the edge of the nanopore via adjusting the incident energy and, by increasing energy, the carbon chains became short and the pore edge became smooth.
• Ed and Ep were found to have relatively weak negative power law dependence on cluster size.
• The cluster collisions with large size led to higher the number of sputtered carbon atoms when all clusters had the same total cluster energy.

References

[1] K. S. Novoselov,A. K. Geim, S. V. Morozov,D. Jiang,Y. Zhang,S. V. Dubonos,I. V. Grigorieva,A. A. Firsov , Science. 306 ( 2004) 666.

[2] T. Lenosky, X. Gonze, M. Teter, V. Elser, Nature.355 (1992) 333.

[3] J.N. Hu, X.L. Ruan, Y.P. Chen, Nano Lett. 9 (7) (2009) 2730.

[4] S. Ghosh, I. Calizo, D. Teweldebrhan, E.P. Pokatilov, D.L. Nika, A.A. Balandin, W. Bao, F. Miao, C.N. Lau, Appl. Phys. Lett. 92 (15) (2008) 151911-1.

[5] A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, and A. K. Geim, Rev. Mod. Phys.81 ( 2009) 109.

[6] D. S. L. Abergel,A. Russell,V. I. Fal’ko, Appl. Phys. Lett. 91 (2007) 063125.

[7] A. Cresti, N. Nemec, B. Biel, G. Niebler, F. Triozon, G. Cuniberti, S. Roche, Nano Research. 1 (2008) 361.

[8] A. K. Geim, Science. 324 (2009) 1530

[9] A. Du, Z. Zhu, S. C. Smith, J. Am. Chem. Soc. 132(9) (2010) 2876.

[10] R. Balog, B. Jørgensen, L. Nilsson, M. Andersen, E. Rienks, M. Bianchi, M. Fanetti, E. Lægsgaard, A. Baraldi, S. Lizzit, Z. Sljivancanin, F. Besenbacher, B. Hammer, T. G. Pedersen, P. Hofmann, L. Hornekær, Nat. Mater. 9 (2010) 315.

[11] T. B. Martins, R. H. Miwa, A. J. R. da Silva, A. Fazzio, Phys. Rev. Lett. 98 (2007) 19680.

[12] Y. M. Lin, C. Dimitrakopoulos, K. A. Jenkins, D. B. Farmer, H. Y. Chiu, A. Grill and P. Avouris, Science. 327 ( 2010) 662.

[13] A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov, A. K. Geim, Rev. Mod. Phys. 81 (2009) 109.

[14 ] D. J. Appelhans, Z. Lin, M. T. Lusk, Phys. Rev. B. 82 (2010) 073410.

[15] G. F. Schneider, Nano Lett. 10(8) (2010) 3163.

[16] P. Russo, A. Hu, G. Compagnini, Nano-Micro Lett. 5(4) (2013) 260.

[17] M. D. Fischbein, M. Drndic, Appl. Phys. Lett.93 ( 2008) 113107.

[18] C. J. Russo, J. A. Golovchenko, Proc. Natl. Acad. Sci. USA. 109(16) (2012) 5953.

[19] S. J. Zhao, J. M. Xue, L. Liang, Y. G. Wang, S. Yan, J. Phys. Chem. C 116(21) (2012) 11776.

[20] Y. C. Cheng, H. T. Wang, Z. Y. Zhu, Y. H. Zhu, Y. Han, X. X. Zhang, U. Schwingenschlögl, Phys. Rev. B. 85 ( 2012) 073406.

[21]H. Araghi, Z. Zabihi, Nucl. Inst. Methods B 298 (2013) 12.

[22] S.J. Plimpton, Journal of Computational Physics 117 (1995) 1.

[23] D.W. Brenner, Phys. Rev. B .42 (1990) 9458.

[24] D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni, S. B. Sinnott, J. Phys. Condens. Mater. 14 (2002) 783

[25] Y. Yamaguchi, J. Gspann, Eur. Phys. J. D. 16 (2001) 103

[26] R. R. Nair, H. A. Wu, P. N. Jayaram, I. V. Grigorieva, A. K. Geim , Science. 335 ( 2012) 442.

[27] N. Inui, K. Mochiji, K. Moritani, N. Nakashima, Appl. Phys. A: Mater. Sci. Process. 98 (2010) 787.

Fig. 1. Incident energy dependence of the reflection and penetration probabilities

Fig. 2. Snapshots of Ar₅₅ clusters collision on graphene sheet : (a) t=0 ps , (b) t= 1 ps , (c) t=6 ps

Fig.3. Final atomic configurations to X–Y plane when the collision energy is: (a)10 ev, and ( b)11 ev

Fig. 4. Final atomic configurations , when the incident energy is: (a)14 ev, and (b)15 ev

Fig. 5. Final atomic configurations to X–Y plane when the incident energy is: (a) 1 Kev, (b) 10 Kev, (c) 20 Kev

Fig. 6. (a) Cluster size dependence of threshold incident energy of defect formation in graphene, (b) Cluster size dependence of threshold energy of penetration into argon cluster

Fig. 7. Dependence of sputtered atoms on kinetic energy of a cluster

Table 1. Lennard–Jones potential parameters