Analysis of S-d Exchange Interactions in Dilute Cu-mn Alloys

Phenomenological analysis of the s-d exchange interactions in dilute Cu-Mn alloys at helium temperatures

• AL-Jalali, M. A.

Abstract:

The S-d exchange interactions in dilute Cu-Mn alloys was studied on concentration ( C ) varying between 10.5 and 2081.8 ppm of Mn in Cu within the ( 0.03K – 4.2K ) temperature range. Using electrical resistivity data on those alloys, the s-d exchange integral ( J_sd ), which is negative, has calculated to show a clear dependence on (Ln C). This dependence, confirming thus the dominance of Kondo effect below 1000 ppm impurity concentration, but above this concentration, we expected an interference between Kondo effect and spin glass regime, which mean that spin glass regime has to prevail more than Kondo effect.

Keywords: s-d interaction; electrical resistivity; J_sd; Kondo effect; spin glass.

PACS: 75: 50, 75:10, 75: 40, 75: 30.

Introduction

The main objective of this paper is to study the huge effects on the coupling between the dilute magnetic impurities (Mn), which gives rise to the formation of local magnetic moments, and the conduction electrons from the host noble metal (Cu).

Electrical resistivity is a great source of information, especially to get the values of the s-d exchange integral J_sd .

For a very dilute alloys (concentration below 100 ppm of Mn), the low-temperature resistivity is dominated by an anomalous Kondo scattering of the conduction electron spin at the local magnetic moments. A typical logarithmic divergence of the resistivity will begin above the Kondo’s temperature( T_K ) until the minimum in the resistivity of Cu-Mn Kondo alloys, where higher temperatures is prevailed, and when the magnetic impurity concentration

Increasing until ( 1 at. %), the interaction between the local magnetic moments and conduction electrons ,which is governed by the Ruderman-Kittel-Kasuya-Yosida (RKKY)[ 1,2,3] interaction will form a spin-glass phase [4].

The method, I have used, to calculate J_sd was the analysis of crude experimental data and by simi-emperical simple calculating, I found that the J_sd decreases logarithmically with concentration and gives a very important information about competition between Kondo effect and spin glass regime[5], which need a deeper study in the future.

Theoretical background

The introduction of few ppm of 3d or 4f magnetic impurity in a non-magnetic matrix leads to an s – d exchange interaction between the spins of the conduction electrons S_e and the Localized magnetic moment S_d of the transition element, which can be described by a Hamiltonian:

Where (J_sd) is the exchange coupling parameter, and is any ordinary scattering from the ion carrying the local moment. With a negative J_sd, the interaction leads to an increase of localized spin disorder resistivity with decreasing temperature.

The competition between the spin disorder scattering and the phonon exhibits the minimum in the resistivity of this regime [6, 7, 8, 9]. Phenomenologically; the above competition is mainly manifested at low temperatures in the form:

Where the spin scattering resistivity, and, ( EF =the Fermi energy),(Z=number of conduction electrons per atom).

In this work, I endeavour to show the behaviour of J_sd in some Cu – Mn alloys, despite the fact that there is the bulk of information has been put forward on these alloys during and after the 1980s, the electrical resistivity one of many sources to provide a powerful means to trace the s – d exchange interaction dominating these alloys.

Analysis of data

Matula and others reported crude data [10, 11, 12] on electrical resistivity and methods of manufacturing of alloys, especially in respect of purity, constituting the major experimental background in this work. They come from direct measurements already carried on Cu – Mn alloys (and many others noble –transition metals alloys) with concentrations ranging from 10.5 ppm to 2081.3 ppm of Mn in Cu within the ( 0.03 – 4.2K ) range [ 11, 12,13 ].

Figure (1) scales versus Ln (T/c) give us by suit fitting an expression like a logarithm of power series solution:

The first two terms (first- order approximation) show a bold line at figure (1), where pure magnetic resistivity could be defined from that lines as a function of ( LnT), and by using a fitting’s programming we can find from the ones of the bold lines a relation as following (figure(2)) :-

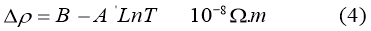
This matches with Hamann’s expression [13, 14, 15, and 16]:

T_k =Kondo temperature

Figure (2) expresses exactly what a compatible between experimental relation (4) and theoretical Hamann’s expression (5) there are.

Definitely, allowing the inclusion of potential scattering effect with single impurity kondo effect, and sharp determination of kondo temperature T_k = 36 mK. Calculated values of J_sd reveal a variation:

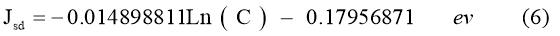
(C is Mn’s concentration in ppm units), as it has shown in figure (3).

Expression ( 6 ) was calculated according to a width of internal field distribution [ 12,16 ] at T_max ( characterize the maximum value of the resistivity at figure(1):

(7)

Results and discussion

As it is shown in figure ( 3 ), above 850 ppm, our calculation to J_sd leads, just as other works do [12,17 , 18 , 19, 20 ] to believe that magnetic transformation takes place from antiferromagnetic to ferromagnetic state and between 860 ppm and 2000 ppm may be a spin glass regime starts to prevail.

When we come back to Kondo’s temperature at Hamann’s expression (5), it is most appropriately to denote that the Kondo’s temperature given as [21]:

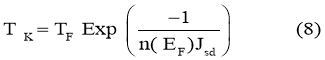
Where, initially, T_F =8.12 10⁴ k, and n (E_F) =0.294 ev^-1.

It seems that T_k is not constant as we noted above, and is not consistent with [22], And has clear dependence on J_sd . Of course, we need more studying to pursue this point.

Finally, as a [instead of] conclusion [put [(Result)], and from figure (3), we can classify a Kondo’s regime in respect of concentration as following:

1. pure kondo regime vanishes at concentration 63 ppm of magnetic impurity (Mn) .
2. Mixed regime ( kondo + SG ) from 63 ppm to 860 ppm.
3. Ideal spin glass from 860 ppm to about 1%.

Conclusion

When we increase the concentration of magnetic impurity, The s-d exchange interactions will move to RKKY interactions, where J_sd will represent a phenomenological order parameter, which reflects a shift of interactions between conduction electrons and localized magnetic moments and discovers the new magnetic transformation from a regime to be other.

1