Amplitude Equations Using Pendulums
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 3596 words | ✅ Published: 11 Sep 2017 |
This report will compare the amplitude formulas thus investigating why they are different. [ar1]The purpose of this report is to find why there is a difference by comparing the two formulas, it will also test why when the amplitude is increased the time-period will consequentially increase. The experiments conducted for this report will use simple methods of taking data to show the complexity of the mathematics behind a pendulum. A number of recommendations are made for the experiments. The hypothesis was found to be supported by the data from the experiments and the background information.
The report will investigate difference between small and large amplitude equation. This will be done by using simple trigonometry with some advanced mathematics.
1.1 What is a pendulum?
“A pendulum is defined as a mass or Bob, connected to a rod.” (Sparknotes)
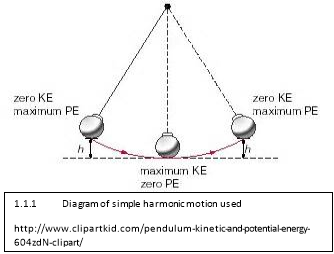 A simple pendulum consists of a Bob connected to a rope or rod traveling in a sector around the pivotal point. The path of the pendulum is called simple harmonic motion[ar2]. The movement of the pendulum can be described as waves as the Bob is at its starting point it has its maximum gravitational potential energy (described in Diagram 1.1.1) when it is at is mirror position (explained further on page 3) it has lost some of its energy but theoretically it has the same energy this means that it is continuous when put on a wave diagram[ar3].
A simple pendulum consists of a Bob connected to a rope or rod traveling in a sector around the pivotal point. The path of the pendulum is called simple harmonic motion[ar2]. The movement of the pendulum can be described as waves as the Bob is at its starting point it has its maximum gravitational potential energy (described in Diagram 1.1.1) when it is at is mirror position (explained further on page 3) it has lost some of its energy but theoretically it has the same energy this means that it is continuous when put on a wave diagram[ar3].
1.2 Effect of Friction
Friction is a dominant effect in a pendulum. It effects the pivotal point, particularly if a rod is used instead of string as it is metal and if it rotates on the pivotal point it well wear down pivotal point or the connection between the two. The other form of friction is air resistance which primary is shown in the decrease of energy and velocity as the Bob goes through the densities of air that the bob travels through but theoretically removing the factor of friction in the equations means that the pendulum will be calculated as if it was in a vacuum.
1.3 The effect of the Bob
 The Bob affects the velocity of the pendulum but not the frequency therefore it does not affect the amplitude of the pendulum but it does effect time osculation. The mass can be used to find the Gravitational potential energy (GPE) (Described further on page 3) of the pendulum at its starting point and at the point where the pendulum finishes half of its oscillation. After both energies, have been calculated they then can be contrasted to find the loss of energy
The Bob affects the velocity of the pendulum but not the frequency therefore it does not affect the amplitude of the pendulum but it does effect time osculation. The mass can be used to find the Gravitational potential energy (GPE) (Described further on page 3) of the pendulum at its starting point and at the point where the pendulum finishes half of its oscillation. After both energies, have been calculated they then can be contrasted to find the loss of energy
1.4 The Effect of the length of pendulum
 The length of the pendulum effects the time period for the longer the length of the pendulum the greater the time it takes for an oscillation, as the bob has a longer path to take compared to a shorter pendulum. The path of the bob can then be calculated by using the following formula for the distance of path.
The length of the pendulum effects the time period for the longer the length of the pendulum the greater the time it takes for an oscillation, as the bob has a longer path to take compared to a shorter pendulum. The path of the bob can then be calculated by using the following formula for the distance of path.
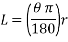
 The ‘L’ in the equation is the circumference of the sector ‘
The ‘L’ in the equation is the circumference of the sector ‘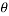 ‘ is the angle from the initial starting point to the point where the pendulum starts to return.[ar4]
‘ is the angle from the initial starting point to the point where the pendulum starts to return.[ar4]
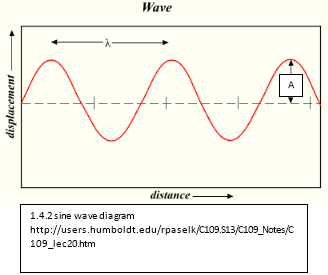 The distance from the origin decrease over time the reason for this is described in next section (1.5). This decrease can be described by a sine wave diagram. The formula for the sin (sine) wave diagrams is:
The distance from the origin decrease over time the reason for this is described in next section (1.5). This decrease can be described by a sine wave diagram. The formula for the sin (sine) wave diagrams is:
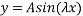
Where ‘A’ is the amplitude of the wave or the radius of a circle, sine is the function of the equation, x is the x axis component and ‘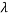 ‘ (lambda) is the wavelength of the movement which is found by:
‘ (lambda) is the wavelength of the movement which is found by:
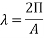
The formula of the wave diagram can be modified to incorporate lambda in the formula, thus formula is:
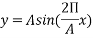
This is simplified to:
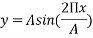
This formula can now be applied to a Cartesian plane to create a sine wave diagram. The sine wave is described further in section 1.6 (the mathematics behind a pendulum).
1.5 The effect of Gravitational potential energy (GPE)
The effect of GPE is a major factor and demonstrates the loss of energy which can then be used to find why the circumference of the sector [ar5]decreases. This decrease in energy can be calculate by the GPE formula which is:
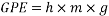
 Where ‘h’ is the height of the mass from the ground in meters, ‘m’ is the mass in kilograms and g is the acceleration due to gravity which is 9.81
Where ‘h’ is the height of the mass from the ground in meters, ‘m’ is the mass in kilograms and g is the acceleration due to gravity which is 9.81 . As the pendulum is reaching its mirror position it has lost some of its energy but the energy lost is small as the angle at which the height is taken must be smaller the initial angle.
. As the pendulum is reaching its mirror position it has lost some of its energy but the energy lost is small as the angle at which the height is taken must be smaller the initial angle.
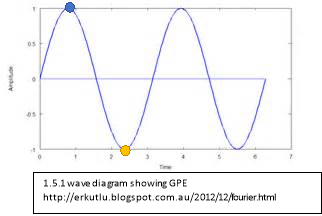
This decrease in energy can be described by wave diagrams. The blue circle on 1.5.1 show the maximum potential energy of the first half oscillation, the yellow circle represents where the oscillation resets and starts a new maximum for the second oscillation in the real world but as this diagram is theoretical it means that there will be no energy increase or decrease therefore the wave on the diagram will go on infinitary.
1.6 The mathematics behind a pendulum
Triangles
A triangle is comprised of 3 line connected so they make an encased shape. The angles [ar6]of a triangle determines the shape and they do not change when the shape is scaled up or down. The angles in this shape always equals 180 degrees but due to rounding [ar7]and miscalculation when applied to pendulums there is usually approximately 0 to 1 degree difference larger than this can mean a wrong answer.

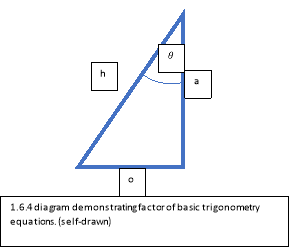
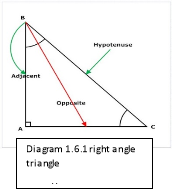 The main triangles that effect a pendulum are right angle and isosceles triangles. A right-angle triangle is described in diagram 1.6.1 which can be used to describe the starting point of the pendulums movement this is described further in ‘Trigonometry’ section.
The main triangles that effect a pendulum are right angle and isosceles triangles. A right-angle triangle is described in diagram 1.6.1 which can be used to describe the starting point of the pendulums movement this is described further in ‘Trigonometry’ section.
An Isosceles triangle can be used to describe the pendulum on its movement. The properties of this type of triangle are that it has two equal sides and has two equal angles this is described by diagram 1.6.2.
Trigonometry
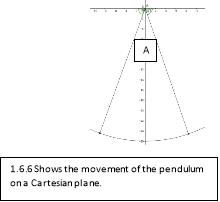
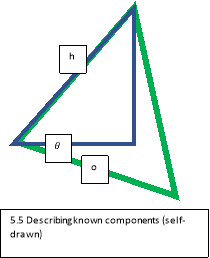
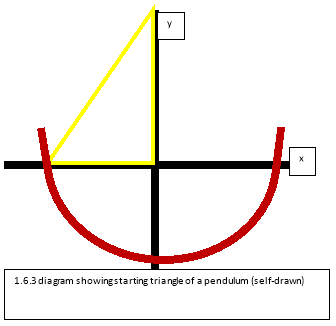 The mathematics are based primarily on trigonometry as the movement of the pendulum can be plotted[ar8] on a Cartesian plane. The yellow triangle in diagram 1.6.3 represents the starting position of the pendulum. The lengths of the triangle can be easily calculated by using basic trigonometry. The following formulas were used:
The mathematics are based primarily on trigonometry as the movement of the pendulum can be plotted[ar8] on a Cartesian plane. The yellow triangle in diagram 1.6.3 represents the starting position of the pendulum. The lengths of the triangle can be easily calculated by using basic trigonometry. The following formulas were used:
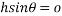
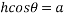
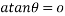
 Where ‘o’ is the opposing side from the angle which is ‘
Where ‘o’ is the opposing side from the angle which is ‘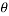 ‘,’h’ is the hypotenuse of the triangle and ‘a’ is the adjacent of the triangle which is described in 1.6.4. The ‘sin, cos, tan’ are the functions of the equations. These formulas can only be used to find the distance on a right-angle triangle which is a triangle with its base and height perpendicular to each other. When the triangle is not a right-angle triangle the sin and co-sin rule is applied.
‘,’h’ is the hypotenuse of the triangle and ‘a’ is the adjacent of the triangle which is described in 1.6.4. The ‘sin, cos, tan’ are the functions of the equations. These formulas can only be used to find the distance on a right-angle triangle which is a triangle with its base and height perpendicular to each other. When the triangle is not a right-angle triangle the sin and co-sin rule is applied.
Degrees and radians
As the pendulum travels in a circular movement. The degrees (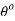 ) can be changed to radians (
) can be changed to radians (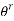 ) as they are equal, when plotted in a circle.
) as they are equal, when plotted in a circle.
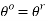
The following formula was used to change degrees to radians:
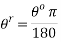
 Once the
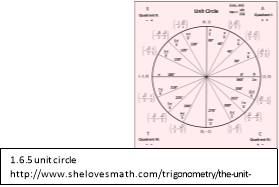
Once the 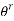 has been calculated it can then be applied to the unit circle (shown in 1.6.5) this means that the movement of the pendulum can also be described on the unit circle as the radius of path of the pendulum will not change it can be graphed on a Cartesian plane from here the points from the origin can be found this is shown in 1.6.6.
has been calculated it can then be applied to the unit circle (shown in 1.6.5) this means that the movement of the pendulum can also be described on the unit circle as the radius of path of the pendulum will not change it can be graphed on a Cartesian plane from here the points from the origin can be found this is shown in 1.6.6.
Sine and Cosine waves
These waves are almost matching except the sine (sin) wave starts at half of it oscillations so at 0 where as a cosine(cos) wave starts at its first peak. The formulas for this waves are also similar.
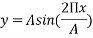
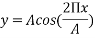
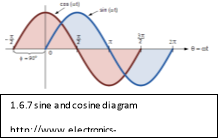 The points on the x-axis which are angle are like points on a unit circle as they make up a isosceles triangle with the hypotenuses always touching the origin (this is shown in 1.6.5). The ‘A’ angle (in 1.6.6) should be converted into radians using the formula for converting degrees to radians which is in ‘Degrees and Radians’.
The points on the x-axis which are angle are like points on a unit circle as they make up a isosceles triangle with the hypotenuses always touching the origin (this is shown in 1.6.5). The ‘A’ angle (in 1.6.6) should be converted into radians using the formula for converting degrees to radians which is in ‘Degrees and Radians’.
1.7 Amplitude
Amplitude is defined in terms of a Cartesian plane is the y component which means it is the same for wave diagrams but in terms of a pendulum the amplitude is the change from the normal which means the distance from where the pendulum is at rest (origin). This distance from the origin can be calculated but are defined by the angle at which the pendulum starts at from the origin which is described further in the following two sections (small and large amplitude formula).
Small Amplitude formula
The theories for small Amplitude can only be used when the angle is equal to or less than 20°. Small amplitude does not affect the time-period. The formula for small amplitude is:
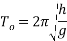
In the formula, the variable ‘h’ is the length of the pendulum (which is shown in 1.6.4) and ‘g’ is the acceleration due to gravity which is 9.81 and
and 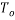 is the amplitude and as this is small amplitude it this fourmula can also canculate the time peroid. This also means that if the mass is changed it will not effect the timeperoid and if the angle is changed and is less thean or equal to 20° it also will not change the period of time of the pendulum.
is the amplitude and as this is small amplitude it this fourmula can also canculate the time peroid. This also means that if the mass is changed it will not effect the timeperoid and if the angle is changed and is less thean or equal to 20° it also will not change the period of time of the pendulum.
Large amplitude formula
Large amplitude theories only work when the initial angle is equal to or greater than 21°. The amplitude also is now effected by the distance at which the pendulum travels. The total angle from where the velocity is 0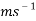 also effects the large amplitude as it dines how far the pendulum has to travel. The large amplitude formula is showed below:
also effects the large amplitude as it dines how far the pendulum has to travel. The large amplitude formula is showed below:
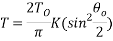
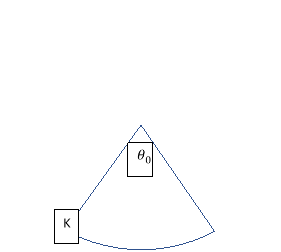
 In the formula, the variable ‘
In the formula, the variable ‘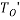 represents the small amplitude formula as this equation is derived from energy equations and the small amplitude formula. The other variables are ‘K’ which is the length of the sector or the distance of the pendulums path in meters and ‘
represents the small amplitude formula as this equation is derived from energy equations and the small amplitude formula. The other variables are ‘K’ which is the length of the sector or the distance of the pendulums path in meters and ‘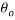 ‘ is the initial angle and its reflection for example if the initial angle is 20° it theoretical reflection is 20° but due to energy loss it means that ‘
‘ is the initial angle and its reflection for example if the initial angle is 20° it theoretical reflection is 20° but due to energy loss it means that ‘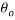 ‘ would be less than 40°.[ar9]
‘ would be less than 40°.[ar9]
 1.8 Theoretical data
1.8 Theoretical data
It was theorized that if the amplitude is increased, the period will then also increase as the distance will change when the length of the pendulum is changed.
Through preliminary trials it was found that if string was used, it would create weightlessness [ar10]and this increased as the angle was increased which would mean that it would fall and lose energy in the process. The other factor that effects the path of the pendulum was as the string as it is not fixed to a linier axis as it will go in a ellipses shape.
The angles for the experiment came from the small amplitude formula [ar11]which is a pendulum with an angle that is equal to or less than 20° this was set as the base angle and was increased in 20 ° increments up to 80°. The angle for the second and third experiments were based on the mean of the angles of the first experiment. This angle was found to be 55°.
The length of the pendulum was decided by the holes in the pendulums arm the weight was then put in one of these holes which changes the centre of mass which was explored in the background research.
The experiment consisted of the following:
 5 different types of steel meccano parts which is shown in the appendix this can be replaced with wooden planks, a metal rod, 3 screw in washers which is shown in 4.1 if a wooden plank is used off cuts can be used to hold the rod in place, a 13 holed meccano piece can be used to replace string, screws the size of the hole of the meccano piece which approximately 3 mm in diameter and nuts, four 50 gram weights and a device to record the experiment and 360° protractor.
5 different types of steel meccano parts which is shown in the appendix this can be replaced with wooden planks, a metal rod, 3 screw in washers which is shown in 4.1 if a wooden plank is used off cuts can be used to hold the rod in place, a 13 holed meccano piece can be used to replace string, screws the size of the hole of the meccano piece which approximately 3 mm in diameter and nuts, four 50 gram weights and a device to record the experiment and 360° protractor.
4.1 Construction
The first step is to build the body or housing:
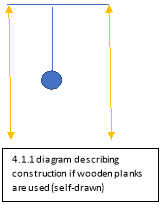 If wood is used the vertical planks should be longer than the length of the pendulum this is shown in 4.2 where the yellow line represent the vertical planks . The planks should form a upside down U when put together. Nails and glue should be used to fasten the frame together. Once this is done a drill will need to be used to drill a hole in the centre of the timber and as straight as possible. The drill bit needs to be 2mm larger than the rod used, this will reduce friction.
If wood is used the vertical planks should be longer than the length of the pendulum this is shown in 4.2 where the yellow line represent the vertical planks . The planks should form a upside down U when put together. Nails and glue should be used to fasten the frame together. Once this is done a drill will need to be used to drill a hole in the centre of the timber and as straight as possible. The drill bit needs to be 2mm larger than the rod used, this will reduce friction.
If meccano was used:
 The corner pieces are fasten together with a with two 11 holed pieces one at the top and a second at the bottom. On the inside of the corners like image 4.3, once the screws are fasten in on the side represented by the blue line in 4.3 they can be connected to the opposing side but no screwed in. the next step was to use two of the 15 hole piece to create a K shape they were screwed in 11 holes from the top and bottom, this means there is 3 hole not being used. They were then put onto the closest corner on the piece represented by the orange line in 4.3 and then screwed in. This was repeated for the opposing side.
The corner pieces are fasten together with a with two 11 holed pieces one at the top and a second at the bottom. On the inside of the corners like image 4.3, once the screws are fasten in on the side represented by the blue line in 4.3 they can be connected to the opposing side but no screwed in. the next step was to use two of the 15 hole piece to create a K shape they were screwed in 11 holes from the top and bottom, this means there is 3 hole not being used. They were then put onto the closest corner on the piece represented by the orange line in 4.3 and then screwed in. This was repeated for the opposing side.
 The two piece were then connected by four 15 hole pieces at the top and bottom of the house. This should look like a rectangle. For stability two 25 hole pieces were added to the back of the housing. They were screwed on side of the housing first three holes from the top and bottom and then screwed to the opposing side so the formed an X which means if one was screwed to the bottom of one side it would be at the top for the other and visa-versa. The middle hole of these two pieces were found and a screwed place in the middle hole and fastened.
The two piece were then connected by four 15 hole pieces at the top and bottom of the house. This should look like a rectangle. For stability two 25 hole pieces were added to the back of the housing. They were screwed on side of the housing first three holes from the top and bottom and then screwed to the opposing side so the formed an X which means if one was screwed to the bottom of one side it would be at the top for the other and visa-versa. The middle hole of these two pieces were found and a screwed place in the middle hole and fastened.
The second step was to create the pendulum and its rod.
If wood was used:
A rod larger than the width of the top plank is pushed through and one of the screw in washers to be put at the end this will help to stop the pendulum from falling out. Another screw in washer is place was placed at the front of the pendulum this is shown in 4.4 where the blue rectangles are the washers and the orange is the plank. The arm of the pendulum can be made out of a wooden ruler or a light timber or string can be used. The arm was then put flat against the washer or tied next to the washer. The third washer was then put on 3 mm away if a wooden arm was used or flat against if string was used.
If meccano was used
The rod was set up the same as if wood was used except a piece of paper coved the arm which was 15 holes long the paper was wrapped the end of the arm with sticky tape and a hole made at the fifth hole from the top of the paper this is the pivotal point and the arm was put on against the second washer and a third washer was put 3mm from the arm.
The last step for the construction was putting the 360° protractor on.
If wood was used:
The protractor can be mounted by form a Y shape with wires, once this was done the wires were then placed into the wood so they were in line with the centre of the rod. The middle of the protractor was then drilled out and put on the wire which was but upwards so the pendulum wouldn’t move.
If meccano was used:
 Two of the 5-hole U pieces where screwed in to top bar which has the rod going through the centre of it. They were screwed 2 holes in this is showed in 4.5. The protractor is then placed in the centre of a 15-hole piece and sticky taped there. This was then screwed to the two 5 holed U pieces, 2 hole at either end which is shown in 4.5.
Two of the 5-hole U pieces where screwed in to top bar which has the rod going through the centre of it. They were screwed 2 holes in this is showed in 4.5. The protractor is then placed in the centre of a 15-hole piece and sticky taped there. This was then screwed to the two 5 holed U pieces, 2 hole at either end which is shown in 4.5.
4.2 Experiment
 The experiment was conducted by placing the completed pendulum on a bench which is shown by the blue rectangle in 4.2.1 and filming the motion of the pendulum (the camera is shown in orange rectangle in 4.2.1). The first experiment was based on what would happen when the angle changes? The angle started at 20° and then went in 20° increments up to 80° this was the independent pendant variable. The dependent variable for this experiment was amplitude particularly the distance from the starting point. The controlled variables were the length of the pendulum which was 26cm, the mass of the pendulum which was 200 grams and the pendulum and its housing. This experiment was conducted by pulling arm of the pendulum back to the selected angle. This can be done in 2 to 3 trials but averages aren’t needed in these equations. The device was then set to record and the pendulum was dropped until it has almost stopped and instead of moving on a left to right movement it will start to go into an eclipse shape this is where the recording was stopped.
The experiment was conducted by placing the completed pendulum on a bench which is shown by the blue rectangle in 4.2.1 and filming the motion of the pendulum (the camera is shown in orange rectangle in 4.2.1). The first experiment was based on what would happen when the angle changes? The angle started at 20° and then went in 20° increments up to 80° this was the independent pendant variable. The dependent variable for this experiment was amplitude particularly the distance from the starting point. The controlled variables were the length of the pendulum which was 26cm, the mass of the pendulum which was 200 grams and the pendulum and its housing. This experiment was conducted by pulling arm of the pendulum back to the selected angle. This can be done in 2 to 3 trials but averages aren’t needed in these equations. The device was then set to record and the pendulum was dropped until it has almost stopped and instead of moving on a left to right movement it will start to go into an eclipse shape this is where the recording was stopped.
The second experiment was to find what the effect of the length has on amplitude? The length started at the first hole where the mass was placed the was put in the next hole to the mass got the 4th hole this was the independent variable. The dependant variable was the same as the previous excrement. The controlled variables were the angle which was 55°, the mass was 100 grams as this was experiments variables where approximately half of the previous experiment and the pendulum and its housing. The experiment was performed in the same way as the previous experiment.
The third experiment was to find what the effect of the mass had on the amplitude? The mass was changed by adding 50-gram weight till there was 200 grams in the hanging from the first slot this was the independent variable. The dependant variable was the same as the previous experiments. The controlled variable was the length which was set at the first hole, the angle which was 55° and the pendulum and its housing. The experiment was performed in the same way as the previous experiments.
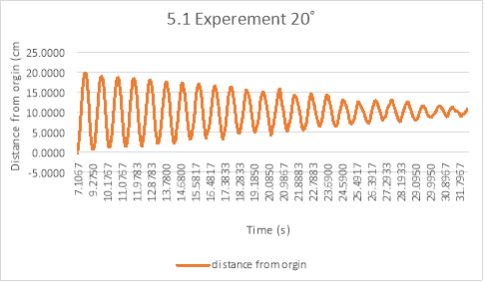
The first set of results are from the experiment investigating what is the effect of the angle on the pendulum?
|
Experiment 20° ( 5.2) |
|
|
Time (s) |
Distance from origin (cm) |
|
7.1067 |
-0.2560 |
|
8.4083 |
0.2195 |
|
8.4417 |
1.1705 |
|
8.4750 |
2.4873 |
|
8.5083 |
3.6578 |
|
8.5417 |
5.4868 |
|
8.5750 |
7.4620 |
|
8.6083 |
9.6201 |
|
8.6417 |
11.8514 |
|
8.6750 |
13.7169 |
|
8.7083 |
15.6921 |
|
8.7417 |
17.1187 |
|
8.7750 |
18.2526 |
|
8.8083 |
19.4597 |
|
8.8417 |
19.7523 |
|
8.8750 |
20.0815 |
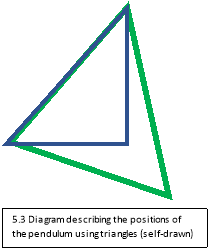
This experiment is where the angle was 20°[ar12] and where the mass was 200 grams and the length of the arm was 26cm. The data was rounded to the 4-decimal place due to the magnitude of the experiment as where was approximately 700 points of data which had approximately 7-8 decimal places. The following calculations were based from the data shown in graph 5.1. These calculations are used to find the amplitude of the first half swing. The data points used for the calculations are shown in table 5.2. The data at the time of 8.8750s is where the pendulum changes it motion and had a velocity of 0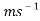 . The position of the pendulum at this position can be explained by a isosceles triangle. This is shown in diagram 5.3 where the blue diagram is the triangle for the starting position and green is the triangle of the first turn.
. The position of the pendulum at this position can be explained by a isosceles triangle. This is shown in diagram 5.3 where the blue diagram is the triangle for the starting position and green is the triangle of the first turn.
 From the amplitude equation shown in background research ‘large amplitude’ section it shows the equation below.
From the amplitude equation shown in background research ‘large amplitude’ section it shows the equation below.
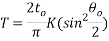
To find the ‘K’ component the length of a sector was used:
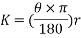
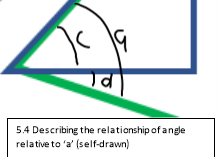 The angle theta is calculated by applying the principles of an isosceles triangle from the background research it states that the two lines are the same and two of the angles are the same as well. This means in terms of the angle that:
The angle theta is calculated by applying the principles of an isosceles triangle from the background research it states that the two lines are the same and two of the angles are the same as well. This means in terms of the angle that:
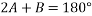
Where ‘A’ and ‘B’ are the angles of the triangle and as there are two angles the same they can be expressed by ‘2 x A’. Angle ‘B’ can then be found by rearranging the above formula.
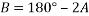
The component 2A was subtracted from both sides of the equation thus cancelling it out on one side. The component of ‘A’ can be calculated by rearranging ‘cos’ function of trigonometry:
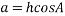
The h component has been divided from both sides of the equation and thus cancelling out h on one side.
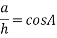
 To cancel cos function from one, side its negative value must be used.
To cancel cos function from one, side its negative value must be used.
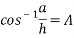
Where 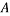 is unknown and h is equal to 26cm which is equal to 0.26 meters (m) and a is the base of the isosceles triangle which is 20.0815 cm or 0.200815 but for these formulas it is not necessary convert to m.
is unknown and h is equal to 26cm which is equal to 0.26 meters (m) and a is the base of the isosceles triangle which is 20.0815 cm or 0.200815 but for these formulas it is not necessary convert to m.
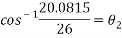
Theta was then calculated to be:
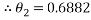
This angle added to its accompany angle this was calculated by:
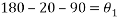
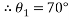
Therefore, the angle ‘A’ is equal to:
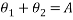
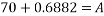
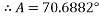
The ‘A’ can now be plug into the initial formula which is:
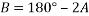
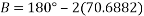
B was calculated to be:
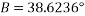
This angle was checked by subtracting the initial angle. This will find if the angle is realistic by the following equation:
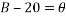
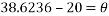
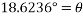
This means that the calculations are correct as the angle must be small than the initial angle due energy loss. The angle can now be put into the following equation which will find the length of the sector and thus the distance of the path of the pendulum.
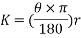
Where 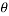 is the angle calculated and described as ‘B’ which is
is the angle calculated and described as ‘B’ which is 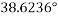 and r is the radius which is 0.26m.
and r is the radius which is 0.26m.
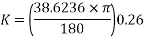
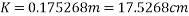
The value of small amplitude formula which is investigated in background research is calculated by:
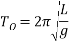
Where ‘g’ is equal to the average gravitational acceleration which is 9.81 and ‘L’ is the length of the pendulum which is 0.26m.
and ‘L’ is the length of the pendulum which is 0.26m.
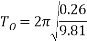
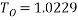
The large amplitude equation can now be used which is:
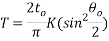
But as this has an initial angle of 20° it means that the value should be smaller than the small amplitude.
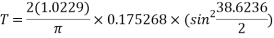
‘T’ was calculated to be:

Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


