Rook Polynomials and Chess

Introduction

Chess is a complex strategical board game. The board on which the game is played is an eight by eight grid. Each player begins the game with 16 pieces: eight pawns, two knights, two bishops , two rooks, one queen, and a single king. Each of the six piece types move differently, and each are able to attack, or remove a certain piece, in different directions. The objective of chess is to checkmate the opposing king by placing one’s own pieces around the king where it is being attacked no matter what action it takes.. While chess is primarily a recreational activity, the complexity of the movement of the pieces has resulted in it having significant mathematical properties. Chess analysis is complicated because of the multitude of movement options open to both players at every single move. Many mathematical chess problems involve discovering how specific placement of pieces can result in none of the pieces attacking each other, I.e. None of the pieces are within the same line of sight.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

One particular variation of these problems is the rook polynomial. The rook piece is able to move horizontally or vertically up to a max of eight squares. In combinatorial mathematics, a rook polynomial generates the combinations of non-attacking rooks; no two rooks are in the same row or column. A board is any layout of squares of a rectangular board with (y) rows and (z) columns. While there are, numerous formulas determining rook placement for rook polynomials, this investigation will look into the method of classifying all quadratic polynomials which are the rook polynomial for some generalized board G.

Rook Movement and Application

As stated, in chess, rooks are able to attack  any square in its line of sight,( i.e. its row or column)  exhibited below

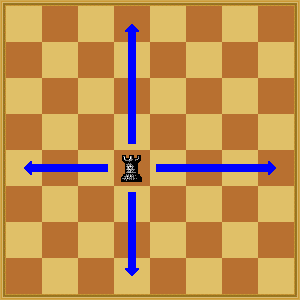
If a rook were to fall in the line of sight of another rook, they would be attacking. Rook polynomials focus on nonattacking rooks. The board of a rook polynomial is defined as a square n x n chessboard, but can also include any subset of a board. For instance, on a 2 x 3 chess board, or an L shaped chessboard would be subset of a regular board. To denote the patterns in which multiple nonattacking rooks can be placed on a generalized board, the variable S can represent the ways to place a number of non-attacking rooks. R will represent the rook, and (G) the size of the generalized board, creating the formula r_s(G). r_s(G) will be stated as r_s when the size of the board (G) as the size of the board will be apparent. For all boards, r₀ will always be equal to one, because it is impossible to set 0 rooks in differing combinations. R₁ will always be the number of squares on the board because rook can be placed anywhere as no other rooks are on the board to attack. R_s = 0 when k is greater than the number of rows or columns on the board, as there will be no way to place all the nonattacking rooks.

The following generalized board provides an example of the equation:

According to our determined parameters, for this particular subset r₀ would again be equal to 1, and r₁ would be equal to the number of squares, in this case six. For r₂ there are 8 ways to place 2 non attacking rooks, demonstrated below.

Three rooks placed on the board only allow for 3 different non-attacking combinations, meaning r₃ equals 3

Since there are only 3 rows for this particular generalized board any r_s>3 as being equal to 0. Using this general principle it is possible to create a polynomial that tracks all of the potential rook combinations on a generalized board. The r_s‘s would be the coefficients of x^s, resulting in the formula:

r₀ + r₁x + r₂x² + …+r_s-1x^s-1+ r_sx^k

The rook placement numbers from the previous generalized board:

r₀ = 1, r₁ = 6, r₂ = 8, r₃ = 3, r₄ = 0, r₅, r₆,… = 0

Resulting in the following polynomial:

1+ 6x + 8x² + 3x³

However it is important to understand that rook polynomials are not unique to a single generalized board. Any board with a similar 3 column lay out would have the same polynomial formula. This leads to the purpose of this mathematics investigation which is to classify all quadratic polynomials which are the rook combinations for a generalized board G.

Determining the Quadratic Polynomial

Since r₀= 1 will always be true, and  r1 = number of squares of (g) the root of the quadratic is:

1 + r₁x + r₂x²

r₁ is determined by board size, therefore it is necessary to discover any r₂‘s where r₃ is equal to 0.  If r₃ is greater than zero, the rook polynomial could potentially be a cubic, or even quartic.

As demonstrated in the previous example, generalized boards with 3 rows will result in polynomials where r₄=0

When examining the requirements of r₄ = 0_, the generalized board must contain two rows of a board and contain squares that are consecutive in each row.

As determined preciously, r₁ is equal to the number of squares on the generalized board. With that information, we can summarize each row of the board as variables (y) and (z). In this case r₁= y+z. With this methodology, (y) and (z) will be placed in a way that the spaces in row (y) are consecutive, and (z) squares are consecutive in the next row. Another important aspect is the number of columns created by (y) and (z). The overlap of the rows will be labeled (p).

Using the number of squares in the example, consider r₁ to be equal to 12. The possible pairs for (y) and (z) are:

1,11; 2,10; 3,9; 4,8; 5,7; 6,6

To create a formula outlining all the potential quadratic equations of a rook polynomial, any of these numbered pairs will work. In the case of 4,8, if none of the rows overlapped, r₂ would be equal to 4×8. To determine r₂ when squares are overlapping, it is necessary to multiply the number of squares in row (y) which are not overlapping by (z), and that to the product of the number of squares overlapping between the two of them and the number of squares not overlapping in row (z). Each square overlap should reduce r₂ by 1. To demonstrate:

2×8+2×7

1×8+3×7

4×7

If a closer look is taken at each of these equations, it is possible to expand it to and relabel the numbers with variables to create a formula. To demonstrate

(3×8) + (1×7) = (4-1)8 + 1(8-1)

(2×8) + (2×7) = (4-2)8 + 2(8-1)

(1×8) + (3×7) = (4-3)8 +3(8-1)

The numerals in these expanded equations can be replaced to reform the formula:

r₂= (y-i)(z) + (p)(z-1)

Simplifying into

r₂ = yz -pz + pz -  p

r₂ = yz -p

We can insert this equation into the rook polynomial already established to create a formula which can calculate all potential rook polynomial combinations.

For example if a generalized board contains row (y) with 6 squares, and row (z) contains 9 squares, with an overlap of p=4, the quadratic polynomial would appear as:

1+(y+z)x +(yz-p)x²

1+(6+9)x +((6×9)-4)x²

1+15x +((54)-4)x²

1+ 15x + 50x²

Therefore the formula to calculate all potential rook polynomial combinations is

1 + (y+z)x + (yz-p)x²

Discussion and Conclusion

Rook polynomials, despite appearing as only a theoretical chess puzzle, actually have a number of practical applications. Various organization problems and layouts can be modeled by the rook problem by equating the objects involved to acting as rooks. A practical application stems from company scheduling. Management may require a specifc number of employees to work their jobs at specific times. However there maybe scheduling issues to ensure no two workers are performing the same job at the same time. A rook polynomial calculation could give insight into the number of combinations of how the workers could be scheduled. The number of workers could represent row (z), and the times available row (y). Each worker must be be at the job and only one time, which is similar to the concept of a rook being at a specific spot that is not attacking any other rook. Depending on the overlap of times and workers available schedule, the formula produce in this investigation could be used to determine the number of combinations.

Another example is if a company desires to hire a certain (y)number of employees on a number (z) different jobs. Each job can only be held by only one employee. By putting both employee number and job number on the rows of a generalized chessboard chessboard, the result is similar to that of a rook’s dilemma. When worker A is appointed to job B, it is like a rook is placed on the square where row (y)overlaps row (z). Every occupation will be performed by a single worker, and every worker is assigned to a single job. Therefore all rows and columns in the pattern will contain only one “rook”, signifying that the rooks will not be attacking one another. The rook polynomial formula could be used to calculate the number of ways the assignments can be executed.

However, the investigation in creating a quadratic rook polynomial formula did have limitations. I was unable to expand the formula to examine greater sized generalized boards, requiring that it not reach cubic or quartic levels. I had initially attempted this, but found that I could not find a generalized rule for each and every combination of a generalized board. For this reason, the application to general life problems is limited. My process could have been improved by investigating further into complex rook polynomials such as the Lagueree polynomial.  Ultimately the complexity of chess allow for both simple and complex mathematical analysis, which can produce formulas which have real life application. Having chess as a visual and interactive tool to explore various concepts of math was a helpful resource when performing this investigation. Not only this, but my own enthusiasm for playing chess and studying the intricacies of the math behind the pieces pushed me to write the investigation.