Cracking Ciphers Through Mathematics

Math Exploration: Cracking different Ciphers

Rationale

From the ancient times to the modern day cryptography has played an important role in our lives. This mathematics exploration is going to look at different ciphers ranging from Monoalphabetic to machine driven cipher. The main use of ciphers is to protect sensitive information when it is being send on paper or digitally. In the 100 BC the Caesar cipher was used by Julius Caesar to send messages to his general which included strategies for war. Now a days these ciphers can be cracked instantly using a computer which makes these ciphers very unsecure. In this exploration I will look at the Caesar Cipher, Vigenère cipher, Hill Cipher and the Enigma Code machine. The Enigma code machine was one of the most fascinating machines I have encountered in my life. It was a complicated machine and could have been unbreakable if the Germans hadn’t had the flaw. After the war ended “It was thanks to Ultra (project associated with the cracking of the Enigma) that we won the war.” Winston Churchill to King George VI. All the ciphers being explored in this exploration have been cracked using mathematics.

Monoalphabetic Substitution Cipher:

Caesar Shift Cipher:

The Caesar Shift Cipher was used by Julius Caesar and thus is named after him. This cipher was used to encrypt military messages. The Caesar cipher is a type of substitution cipher. The Caesar cipher was decrypted 800 years after its creation by an Arab mathematician Al-Kindi using the process of frequency analysis.

The Caesar Shift Cipher used the English letters and shifted each letter by 3 places to encrypt it. For Example: In this example let the alphabet be x and the cipher text will be x+3.

The plain text is “attack the castle at dawn”. This is currently plain text and if Caesar send it to his military his enemies could easily find out. But when it is encrypted applying the formula

e(x) = (x + k) (mod 26)

Using the formula above where x is the plain text number and k is the number by which the cipher is shifted and modulo 26 is the total number of alphabets in the English language. This leads us to the encrypted message from Caesar would be “dwwdfn wkh fdvwoh dw gdzq” this message could be only decrypted only by the people who knew the shift value. There are only 25 possibilities in this cipher which makes it relatively easier to crack than other ciphers. In the modern age this type of cipher can be decoded in seconds making the message being transmitted very unsecure.

Breaking the Caesar Cipher

This Cipher was cracked using a method called frequency analysis which bases on the some letters occurring more than other. This process was discovered by Al-Kindi in the 9^th century.

As we can see from the frequency analysis of the English language there is a lot of repetition of the word e. Thus making it easier to crack the Caesar Cipher or any other similar kind of substitution ciphers. To crack this cipher when we are looking at the encrypted test find the letters that are occurring the most which will tell us the shift needed for the cipher text.

For example: “nmfajfxjhwjyrjxxfljktwymjljsjwfq”

Using the text without spaces makes it harder for the person trying to decode without the key. Now as we can see from the encrypted message above if we use the frequency analysis method we find that j repeats 8 times and if we assume that j is represented as e then it has a shift of 5 alphabets in this cipher.

e(x) = (x – k) (mod 26)

Now we use the above equation in which we now subtract the shift and multiply with modulo 26. After decrypting the final message we have is “ihaveasecretmessagefromthegeneral”.

Polyalphabetic Substitution Cipher:

Vigenère Cipher:

The Vigenère Cipher method was originally described by Giovan Battista Bellaso in his 1553 book La cifra del. Sig. Giovan Battista Bellaso. This method was later misattributed to Blaise de Vigenère in the 19^th century thus giving the cipher the name “Vigenère cipher”. Vigenère cipher is method that uses a series of different Caesar ciphers based on a lettered keyword. This cipher is a form of polyalphabetic substitution.

In this cipher we make a key before encrypting the message so that it is a bit more secure. In this method the key shifts the alphabets according to its position. In this encryption the key needs to be known for the person decrypting it because there are about 26ⁿ possibilities where n is the number of letters in the string.

For example let the code be: “mybirthdayisinjanuary” and let’s take the key to be “math”

Thus the encrypted text cannot be broken easily and if someone tried without a key there are 26⁵ ≈ 1.2 X 10⁷ possibilities unlike the Caesar cipher with just 25 possibilities.

Decrypting the Vigenère cipher:

The first crack for the Vigenère cipher was discovered in 1854 by British Cryptographer Charles Babbage. This Vigenère cipher can now be easily cracked in the modern day cryptography using the Kasiski analysis method to crack this cipher. To crack a Vigenère cipher the most difficult part is to find the length of the key.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

The method used to find the key uses repeating patterns and finds the distance between the patterns. This can be done using the Crypto-Corner tool which will find the periods of the repeating patterns. Then using the frequency analysis we can decrypt the message.

For example let the encrypted code be “GZEFWCEWTPGDRASPGNGSIAWDVFTUASZWSFSGRQOHEUFLAQVTUWFVJSGHRVEEAMMOWRGGTUWSRUOAVSDMAEWNHEBRJTBURNUKGZIFOHRFYBMHNNEQGNRLHNLCYACXTEYGWNFDRFTRJTUWNHEBRJ”

Now to decrypt it just put the code in the crypto-corner tool and it gives us a repeating period of 3. Which leaves us with 3 separate Caesar shifts to decrypt this message using the frequency analysis.

The image above shows the encrypted message and the decrypted message. It also shows us the key used to encrypt this message. This was done using frequency analysis for three Caesar shift ciphers. After the cipher is decrypted the key is discovered to be “NSA”. It is a relatively easy cipher to crack but can be time consuming using a computer brute force attack. The main uses of Vigenère cipher was in the military to send secrets to allies so the enemy could not decrypt it easily. As this cipher took me around 4 minutes to crack using the tool.

Diagraph Substitution Cipher:

Hill Cipher:

The Hill cipher is a polygraphic substitution cipher which is based on linear algebra. It was invented by Lester Hill in 1929 it was the first polygraphic cipher in which it was possible to operate on more than three symbols at once.

The main idea behind hill cipher is to convert the plain text into numbers and separate into blocks and then covert them into column matrix. Then it is multiplied by a key of the form .The result of this is multiplied by modulo 26 which keeps the numbers in a cycle of 0 to 25. The matrix in the form obtained by this method is then covered back to a non-column form and then to plain text.

For example let’s take the word “TROJANHORSES” which converts to 19, 17, 14, 9, 0, 13, 7, 14, 17, 18, 4 and 18.

Now let the key that is known by the person who is encrypting and decrypting be

.

Thus now we divide the plain text numbers into two column matrix and multiply by our key.

Thus this encryption gives us a cipher text “ETRVNNLGBUOU” from the original text “TORJANHORSE” the Hill cipher overcomes the problems related to frequency analysis associated with the Caesar shift cipher.

Decryption of Hill Cipher:

For the decryption process of the Hill cipher the inverse of the key is done. To make it into the form thus making the encryption matrix key used in the example into the form.

Now we calculate the determinant of the encryption key is = (5*3) – (3 * 2) = 9

A^-1 = 9^-1 mod 26

To get rid of the mod 26 we take modulo inverse of the determinant and thus it gives us. This can sometimes be a problem because if the determinant of a matrix is not a co-prime number to the 26. Then it is not invertible and thus we cannot decipher the text.

A^-1 = 9^-1

Thus 9-1 mod 26 is 3 as per the modulus tables of multiplicative inverse modulo and modulo of

A^-1 = 3

A^-1 = = mod 26

The decryption key now is now we multiply the cipher text “ETRVNN” which will give us “TROJAN”

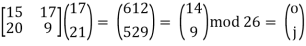
Thus the deciphered text is ‘TROJAN” which makes this cipher weak if a person is aware of the keys as it might not take a lot of time to do this by hand. Also nowadays the computer can easily crack this cipher given the key is present with the person cracking it. Cracking this cipher can be easily done these days using a brute force attack on the cipher and it took me around 40 seconds to break the code. Which indicates it is relatively insecure to use hill cipher to code the text today to send secret messages as it can be intercepted and easily decrypted.

Machine Driven Cipher:

Enigma Code Cipher:

The Enigma code cipher was invented by the German engineer Arthur Scherbius at the end of World War I. It was used to send encrypted messages to German U-Boats and communicate between German military. During the World War II it was adopted by the Nazi Germany to send and receive encrypted messages from German army or the Air Force.

The Enigma machine uses a keyboard on which the operator types the message he wants to encrypt. Then the message goes to the 3 rotors these rotors combine of 3 different types of rotors a fast rotor which turns when a letter is types. Then a medium rotor which turns when the fast rotor completes a revelation and the slow rotor which rotates when the medium rotor completes a revolution. After the plain text has gone through the three rotors it reverses and goes again through the slow, medium and fast rotor to the plug board. The German army had a choice of choosing 3 rotors from a set of 5 rotors and the rotors could be set in any orientation.

The number of ways the rotors can be positioned from a set of 5 are = 60 possibilities.

The different starting positions of the rotors as they were changed every day giving 26³ = 17576 possibilities of different codes. The 1-26 numbers on the three rotors represent the alphabets from a-z. After the letter is plain text in pressed on the enigma it goes through plug board to the 3 rotors and gets ciphered. Then the cipher text goes back to the plug board usually the plug board would have been connected to the 10 wires which connected 20 alphabets together. Thus if the ciphered text is connected to a wire it would light up the alphabet it might be connected to.

For example if the letter h was pressed it would go to the plug board then through the circuit it goes through the 3 rotors which cipher the plain text 3 times. After that it returns back to the plug board as letter M which is connected to the letter A and thus the bulb connected to letter A lights up. The number of possibilities on the plug board are

The possibilities that are displayed above are the total theoretical possibilities for changing the plug board setting in different orientation giving ways. The total number of possible ways the settings of the enigma could be changed into are:

(Possibilities the settings could be changed into. Thus making it really difficult to solve by pen and paper. The use of computer is really essential to break a code which has been encrypted using enigma.

Decrypting Enigma code cipher:

To decrypt the enigma code the German army distributed a sheet which contained the settings for each day of the month. So the side receiving the code can set the settings and then type the code using the keyboard which reverses the process and after typing the plain text blinks on the light panel.

The enigma code was cracked by the allies during the World War II by the Alan Turing and his team consisting of mathematicians. The flaws that helped decrypting the enigma code cipher was that if a letter was typed it wouldn’t place the same letter in the cipher text. For example if a person typed B in code the cipher would be something like X but never B.

To break the code Alan Turing built a bomb machine which checked all the Possibilities of settings and took only 20 minutes to break the code.

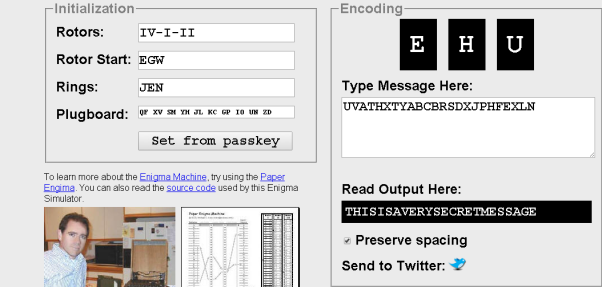
For example let the plain text message be “THISISAVERYSECRETMESSAGE” as I don’t have access to an enigma machine using an online simulator. The cipher text using the rotor order as VI-I-II, the rotor start as EGW (5, 7, 23), the ring setting as JEN and the plug board setting as QF XV SM YH JL KC GP IO UN ZD. Now when we encode this message we use the encoding setting as EHU and the cipher text is “UVATHXTYABCBRSDXJPHFEXLN”. To decrypt this message either a brute force attack which took around 7 minutes or if the settings are provided use a decryption tool online to decrypt the cipher text to plain text.

Bibliography

Ekert, A. (n.d.). Cracking codes. Plus.maths.org. Retrieved October 29, 2014, from http://plus.maths.org/content/cracking-codes

Caesar cipher. (n.d.). Princeton University. Retrieved October 29, 2014, from https://www.princeton.edu/~achaney/tmve/wiki100k/docs/Caesar_cipher.html

Casselman, B. (n.d.). Feature Column from the AMS. American Mathematical Society. Retrieved October 29, 2014, from http://www.ams.org/samplings/feature-column/fcarc-enigma

Clark, D. R. (n.d.). Vigenère Cipher. Crypto Corner. Retrieved October 29, 2014, from http://crypto.interactive-maths.com/vigenegravere-cipher.html#intro

Clark, D. R. (n.d.). Hill Cipher. Crypto Corner. Retrieved October 29, 2014, from http://crypto.interactive-maths.com/hill-cipher.html#2x2encypt

Count On :: Codebreaking :: The Vigenère Cipher. (n.d.). Count On :: Codebreaking :: The Vigenère Cipher. Retrieved October 29, 2014, from http://www.counton.org/explorer/codebreaking/vigenere-cipher.php

Crypto. (n.d.). Practical graphy. Retrieved October 29, 2014, from http://practicalcryptography.com/ciphers/hill-cipher/

Crypto. (n.d.). Practical graphy. Retrieved October 29, 2014, from http://practicalcryptography.com/ciphers/vigenere-gronsfeld-and-autokey-cipher/

Crypto Analysis to Crack Vigenère Ciphers. (n.d.). IB Maths Resources. Retrieved October 29, 2014, from http://ibmathsresources.com/2014/05/31/crypto-analysis-to-crack-vigenere-ciphers/

Cunningham, Z., & Mabey, M. (n.d.). Security Ninja. Security Ninja. Retrieved October 29, 2014, from http://csilm.usu.edu/~securityninja/index.psp

Ellis, C. (n.d.). Exploring the Enigma. Plus.maths.org. Retrieved October 29, 2014, from http://plus.maths.org/content/exploring-enigma

Enigma machine. (2014, October 27). Wikipedia. Retrieved October 29, 2014, from https://en.wikipedia.org/wiki/Enigma_machine

Lyons, J. (n.d.). Crypto. Practical graphy. Retrieved October 29, 2014, from http://practicalcryptography.com/cryptanalysis/

Simpson, R. (n.d.). Cipher Machines. Cipher Machines. Retrieved October 29, 2014, from http://ciphermachines.com/enigma

Singh, S. (n.d.). The Black Chamber. – Caesar Cipher. Retrieved October 29, 2014, from http://www.simonsingh.net/The_Black_Chamber/caesar.html

Singh, S. (n.d.). The Black Chamber. Vigenere Cipher. Retrieved October 21, 2014, from http://www.simonsingh.net/The_Black_Chamber/vigenere_cipher.html

Sutherland, S. (n.d.). 3 The Caesar Cipher and Modular Arithmetic. 3 The Caesar Cipher and Modular Arithmetic. Retrieved October 29, 2014, from http://www.math.sunysb.edu/~scott/papers/MSTP/crypto/3Caesar_Cipher.html

Vestergaard, E. (n.d.). The German cipher machine Enigma. Enigma. Retrieved October 29, 2014, from http://www.matematiksider.dk/enigma_eng.html

Vigenère cipher. (n.d.). Vigenère cipher. Retrieved October 22, 2014, from https://www.princeton.edu/~achaney/tmve/wiki100k/docs/Vigen%C3%A8re_cipher.html