How Does the Idea of Limits Make the Calculus Precise?

How does the idea of limits make the calculus precise?

In this essay, I will be discussing the topic of differentiation and how the ideas of the calculus were criticised. I will be giving an overview of how calculus can be explained and explaining the idea of limits and the infinitesimal number.

The Calculus controversy between Newton and Leibniz is known to be one of the greatest mathematical disputes due to the importance and accomplishment of such findings. On contrary, their findings introduced the foundations of calculus which is more commonly referred to as differentiation and integration. Their findings were criticised heavily by many people but especially a mathematician known as Berkeley. Yet Berkeley acknowledged the truths derived from calculus, he was quick to pounce and to try disproving their theories. Berkeley was a great mathematician himself, subsequently his work was to find faults and cracks in other people’s work and publicly expose them. Berkeley accepted the ideas of calculus but found the idea problematic due to the use of the infinitesimal number.

(Wisdom ,1953, pp. 22-25) denotes that philosophers supposed that the purpose of Berkley’s findings was to indulge in a futile trial of strength with newton, this can suggest that Berkeley was jealous of newton but can also suggest that he cared more about taking newton down rather than the mathematics involved. Wisdom also pointed out that Berkeley attacked the logic of the infinitesimal number saying that the value of zero is seen as a finite quantity of no size and also a zero-increment value. Due to the quantity of zero not being consistent, Berkeley dismissed this problem as “ghosts of departed quantities”. This idea means that the effects of zero being infinitesimally small and zero itself suggests that newtons work was self-contradictory and the effects of this remained in the calculations after it was supposedly made to vanish. However, Berkeley didn’t understand that newtons findings were only the starting foundations with an expansion to the theory of limits. Wisdom goes on to explain that despite the destructive criticism of Berkeley, it was extremely important as the errors he investigated were compensated for with the introduction of limits and the movement away from the infinitesimals.

(Grabiner 1997, pp. 393-394) insinuates that Berkeley attacked the logical validity of the calculus adding to his assault on Newton as a person and a mathematician. Berkeley is described to be witty and unkind when criticising newtons mathematical practises.  Berkeley also accuses mathematicians of being hostile to religion which is considered to be irrelevant when confronting a mathematical theory. Subsequently, Berkeley’s approach to his challenge on newton was not a mathematical one, yet an attack on him and the people who supported newton. 

Theoretically speaking in terms of real numbers, the infinitesimal number is missing as it is not regarded as a real number. Infinitesimal numbers can be referred to as quantities that approach to zero or can be expressed as variable quantities. The word infinitesimal means that something is so small that it is impossible to measure or calculate. An infinitesimal object is one that cannot be measured feasibly but does never equal zero.

Limits are a measurement that stays in our dimension and maintains the supposedly perfect illusion of such model. Infinitesimals are much smaller and accurate than limits in such that models are built in another dimension, much more accurate and smaller and maintains the illusion perfectly in the normal dimension.

Infinitesimals have a rigorous foundation.

(Bolton 1995, pp, 1-3.) illustrates that differentiation is a technique in mathematics to calculate or determine the rate of change of a function. Where a function is a relationship between two quantities that change interdependently. With limits installed, the value of the function is investigated when the independent variable gets extremely close to a particular value. With regards to limits, mathematicians can use differentiation to work out the rate of change between two points known as limits, these limits enable the study of something that can be measured.

Integration is used to work out the are under a graph at certain points.

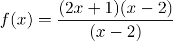Showing that limits exist

If we take the function,

For when x=2.

If we sub in 2 for x, then the function gives an infinite number, this Is because the numerator which equals 5 is divided by 0 which cannot be calculated as there are infinite numbers the answer can be.

Alternatively cancelling out the (x-2) yields the same denominator of 0. For this to happen x cannot be equal to 2, it must be equal to anything other than 2 to cancel out the same terms of (x-2). Then we are left with:

f(x)=(2x+1)

This simpler function can now predict that;

f(2)=5

So, the prediction for this even is 5, this number was calculated using behaviour outside of the event to predict the actual outcome behaviour of the event.

To work out the validity of the event, we need to input an accuracy threshold or a range to stay within the given accuracy.

For example, I will place an accuracy threshold of ±1 so will give answers either side of 5, so will be 4 and 6. For this to be, x must equal 1.5 or 2.5 to produce such numbers. As a result, this function is said to limit 2, this is because when x equals 2, the function depicts an infinite nature. Thus, f(x) can be made extremely close to the limit of 2 just by making x especially close to 5.

In chapter 4 of ‘MATHEMATICS A VERY SHORT INTRODUCTION’ , Gowers talks about the ideas of limits and infinity and explains to how to deal with such difficulties. He starts with talking about the concept of the square root of a number. Gowers illustrates that the square root of 2 is roughly 1.41421356 and explains that this number is accepted to being equal. The root of 2 lies between 1.4 and 1.5 and so the decimal expansion starts.

1.41421356²=1.9999999933878736

1.41421357²=2.0000000216721449

If the decimal expansion keeps increasing there will be an infinite increase of the number 9 so 1.9999999… recurring is considered to be equal to 2; this is an accepted truth of mathematics.

Another scenario Gowers investigated was one associated with speed, distance and time. Gowers illustrated to his audience a scenario that shows calculus cannot calculate the average of speed of a car but can calculate the average speed of a car during that time over a distance. Consequently, this does not tell you the speed of a car at any moment in time. In order to overcome this hurdle, Gowers talks using infinitely small periods of time and calculating how many miles the car has travelled in such small time. This “ridiculous fantasy” as Gowers defines it creates numerous problems in the mathematical world and portrays similar problems to such ideas that 1.9 recurring is the same as 2. Subsequently, working out the speed of a car in such a small time is regarded as invalid when a time of 0 seconds is used. However, exploiting the fact that in a small period of time, cars do not actually accelerate much at all, so using accurate measuring devices and an appropriate time frame, a close approximation can be calculated and yet wont yield the correct answer, but will provide us with an answer mathematically correct. This is also reminiscent of mathematical models in the fact that they yield a scientifically accepted approximation of a natural phenomenon but is also not utterly one hundred per cent accurate.

Infinity is involved once again and due to its infinite nature, limits are suggested to be put in place which is a sequence of finite decimals that can be used to calculate the approximation for the scenario that involves an infinite decimal count.

Gowers then goes onto explain the calculations that involve the area of the circle using ϖr². The area of an object is described as the “amount of stuff” that a shape beholds. The issue regarding the calculations of the area of circles is due to its curved nature, therefore, it is impossible to fit triangles into such shapes. A circle never has a straight line and as triangles do, there will always be a small area unaccounted for as shown in the diagram to the left, unless an infinite number of thin triangle is used, which is understandingly impossible to calculate.
 

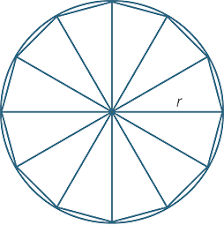
Gowers estimates the area of this circle using numerous squares, the main problem is that many squares lie partly inside the shape. The obvious way to improve the accuracy of the estimate is to make the squares smaller, yet the result of this just makes the approximation closer to a specific number that cannot be worked out due to the infinite number of squares that there has to be to be distributed over the whole circle. The area of a circle is mathematically accepted if a tolerable percentage of error is used. To get the exact final answer, an infinite amount of infinitely small squares must be used which is impossible to calculate.

If you draw a straight tangent to the circle at any point on the circumference, the gradient of the tangent will equal the gradient of the circle line at an infinitely small value, therefore there would need to be an infinite number of squares for there to be an accurate calculation of the circle area.

To conclude on this overview of chapter 4, Gowers has provided us with a “fruitful” interpretation about the ideas of infinity and the use of limits and how they can provide us with an approximation rather than defining a scenario completely in one go. (Gowers, 2006, pp56-69.)

Differentiation is the process of acquiring the derivative of a function or working out the rate of change of an event; for example, the acceleration of a car or the rate of change with respect to x and y on a graph/ the gradient of the line.

Examples of differentiation

y = x²

dy/dx = 2x

The dy/dx refers to differentiating the function of y with respect to x. The derivative is then used to work out the rate of change of the function.

When x=10, dy/dx is equal to 20, this means at this value, the gradient of the line 20 meaning that at this instantaneous point, as the x value is increased by 1, the value of y increases by 20.

Differentiation from first principles

With the example from above, I used the shortcut method to differentiate y=2x, this shortcut method is derived from the first principle method.

For example:

For y=x²

$f^{‘\left(x\right)}=\lim f\left(x+h\right)–f\left(x\right) /h$

                as h limits to 0.

$f^{‘\left(x\right)}=\lim \left({\left(x+h\right)}^2\right)–f\left(\mathit{x²}\right) /h$

            as h limits to 0.

$f^{‘\left(x\right)}=\lim (x^2+h^2+2\mathit{xh}–\mathit{x²}) /h$

        as h limits to 0.

$f^{‘\left(x\right)}=\lim (2x+h)$

                                      as h limits to 0

$f^{‘\left(x\right)}=2x$

As h limits to 0, this means that the value of h can be infinitesimally small but will never equal to due to the fact that the equation cannot be divided by 0. ‘h’ can never be 0 because differentiation is the rate of change between two variables and if h equals to 0, it suggests there has been no change, so differentiation cannot take place.

To conclude, Leibniz and newton introduced the foundations of calculus and although it was heavily criticized for its validity, it is widely used today and is being taught to millions of children in schools every year all over the World. Their findings are substantial in the mathematical world but if it wasn’t for the thorough assessment and criticism of their work by Berkeley, then calculus wouldn’t be fully intelligible to what it is today. Limits are a way of expressing a function that gets extremely close to a number until it has an infinite number of solutions. Newton and Leibniz graced us mathematicians with the brilliance of differentiation and integration and enabled other more recent mathematicians to venture on to different sub topics and develop their understanding of calculus.

Reference List

• Bolton, W. (2014) Differentiation and integration. New York: Routledge.
• Grabiner, Judith V. “Was Newton’s Calculus a Dead End? The Continental Influence of Maclaurin’s Treatise of Fluxions.” The American Mathematical Monthly, vol. 104, no. 5, 1997, pp. 393–410. JSTOR, www.jstor.org/stable/2974733.
• Gowers, T. (2002) MATHEMATICS A VERY SHORT INTRODUCTION. New York: Oxford University Press Inc.
• Wisdom, J. O. “Berkeley’s Criticism of the Infinitesimal.” The British Journal for the Philosophy of Science, vol. 4, no. 13, 1953, pp. 22–25. JSTOR, www.jstor.org/stable/686042.

Bibliography

• https://en.wikipedia.org/wiki/Leibniz%E2%80%93Newton_calculus_controversy
• https://en.wikipedia.org/wiki/The_Analyst#CITEREFGrabiner1997
• https://plus.maths.org/content/news-world-maths-attacks-foundations-calculus