Hopf Algebra Project

Petros Karayiannis

Chapter 0

Introduction

Hopf algebras have lot of applications. At first, they used it in topology in 1940s, but then they realized it has applications through combinatorics, category theory, Hopf-Galois theory, quantum theory, Lie algebras, Homological algebra and functional analysis.

The purpose of this project is to see the definitions and properties of Hopf algebras.(Becca 2014)

Preliminaries

This chapter provides all the essential tools to understand the structure of Hopf algebras. Basic notations of Hopf algebra are:

1. Groups
2. Fields
3. Vector spaces
4. Homomorphism
5. Commutative diagrams

1.Groups

Group G is a finite or infinite set of elements with a binary operation. Groups have to obey some rules, so we can define it as a group. Those are: closure, associative, there exist an identity element and an inverse element. Let us define two elements U, V in G, closure is when then the product of UV is also in G. Associative when the multiplication (UV) W=U (VW) ꓯ U, V, W in G. There exist an identity element such that IU=UI=U for every element U in G. The inverse is when for each element U of G, the set contains an element V=U^-1 such that UU^-1=U^-1U=I.

2.Fields

A field Ҝ is a commutative ring and every element b ϵ Ҝ has an inverse.

3.Vector Space

A vector space V is a set that is closed under finite vector addition and scalar multiplication. In order for V to be a vector space, the following conditions must hold ꓯ X, Y ϵ V and any scalar a, b ϵ Ҝ:

• a(b X) = (a b) X
• (a + b) X=aX + bX
• a(X+Y)=aX + aY
• 1X=X

A left ideal of K-algebra is a linear subspace that has the property that any element of the subspace multiplied on the left by any element of the algebra produces an element of the subspace. We say that a subset L of a K-algebra A is a left ideal if for every x and y in L, z in A and c in K, we have the following:

1. X +y is in L
2. cx is in L
3. zâ‹… x is in L

If we replace c) with x⋅ z is in L, then this would define a right ideal. A two-sided ideal is a subset that is both a left and a right ideal. When the algebra is commutative, then all of those notions of ideal are equivalent. We denote the left ideal as ⊳.

4.Homomorphism

Given two groups, (G,*) and (H,°) is a function f: G→H such that ꓯ u, v ϵ G it holds that

f(u*v)=f(u)°f(v)

5.Commutative diagrams

A commutative diagram is showing the composition of maps represented by arrows.

The fundament operation of Hopf algebras is the tensor product. A tensor product is a multiplication of vector spaces V and W with a result a single vector space, denoted as V   W.

Definition 0.1

Let V and W be Ҝ-vector spaces with bases {e_i } and {f_j } respectively. The tensor product V and W is a new Ҝ-vector space,   V    W with basis { e_i f_j }, is the set of all elements v   w= ∑ (c_i,j e_i   f_j ). c_i,j ϵҜ are scalars.

Also tensor products obey to distributive and scalar multiplication laws.

The dimension of the tensor product of two vector spaces is:

Dim(V  W)=dim(V)dim(W)

Theorem of Universal Property of Tensor products 0.2

Let V, W, U be vector spaces with map f: V x W → U is defined as f: (v, w) →vw.

1. There exists a bilinear mapping b: V x W → V  W , (v,w) → v    w
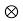2. If f: V x W → U is bilinear, then there exist a unique function, f: V  W→U with f=f°b

 Extension of Tensor Products0.3

The definition of Tensor products can be extended for more than two vectors such as;

V₁ âŠ-  V₂âŠ-   V₃ âŠ-  …..âŠ-  V_N = ∑( b_iv₁âŠ-  v₂âŠ-  ….âŠ-  v_n )  (Becca 2014)

Definition0.4

Let U,V be vector spacers over a field k and ν ϵ U⨂V. If ν=0 then Rank (ν) =0. If ν≠0 then rank (ν) is equal to the smallest positive integer r arising from the representations of ν= ∑u_i ⨂ v_i ϵU⨂V for i=1,2,…,r.

Definition0.5

Let U be a finite dimensional vector space over the field k with basis {u₁,….,u_n}  be a basis for U. the dual basis for U^*is {u¹,….,uⁿ} where uⁱ(u_j)= δⁱ_j for 1≤I,j≤n.

Dual Pair0.6

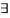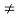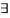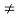A dual pair is a 3 -tuple (X,Y,<,>) consisting two vector spaces X,Y over the same field K and a bilinear map, < , >: X x Y→K with ꓯx ϵ X{0} yϵY: 0 and ꓯy ϵ Y{0} xϵX: 0

Definition0.7

The wedge product is the product in an exterior algebra. If α, β are differential k-forms of degree p, g respectively, then

 α∧β=(-1)^pq β∧α, is not in general commutative, but is associative,

(α∧β)∧u= α∧(β∧u) and bilinear

(c₁ α₁+c₂ α₂)∧ β= c₁( α₁∧ β) + c₂( α₂∧ β)

α∧( c₁ β₁+c₂ β₂)= c₁( α∧ β₁) + c₂( α∧ β₂).    (Becca 2014)

Chapter 1

Definition1.1

“Let (A, m, η) be an algebra over k and write m^op (a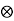b) = ab ꓯ a, bϵ A where m^op=mÏ„_Α,Α. Thus ab=ba ꓯa, b ϵA. The (A, m^op, η) is the opposite algebra.”

Definition1.2

“A co-algebra C is

1. A vector space over K
2. A map Δ: C→C âŠ-  C which is coassociative in the sense of ∑ (c₍₁₎₍₁₎ âŠ-   c₍₁₎₍₂₎ âŠ-  c₍₂₎)= ∑ (c₍₁₎ âŠ-   c₍₂₎₍₁₎ âŠ-  c₍₂₎c₍₂₎ )   ꓯ cϵC (Δ called the co-product)
3. A map ε: C→ k obeying ∑[ε((c₍₁₎)c₍₂₎)]=c= ∑[(c₍₁₎) εc₍₂₎)] ꓯ cϵC ( ε called the counit)”

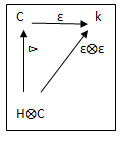
Co-associativity and co-unit element can be expressed as commutative diagrams as follow:

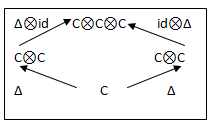
Figure 1: Co-associativity map Δ

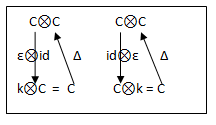
Figure 2: co-unit element map ε

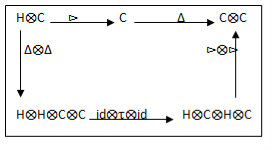
Definition1.3

“A bi-algebra H is

1. An algebra (H, m ,η)
2. A co-algebra (H, Δ, ε)
3. Δ,ε are algebra maps, where HâŠ-  H has the tensor product algebra structure (hâŠ- g)(h^‘âŠ-  g^‘)= hh^‘âŠ-   gg^‘ ꓯh, h^‘, g, g^‘ ϵH. “

A representation of Hopf algebras as diagrams is the following:

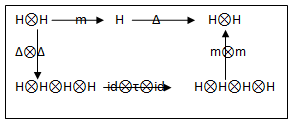
Definition1.4

“A Hopf Algebra H is

1. A bi-algebra H, Δ, ε, m, η
2. A map S : H→ H such that ∑ [(Sh₍₁₎)h₍₂₎ ]= ε(h)= ∑ [h₍₁₎Sh₍₂₎ ]ꓯ hϵH

The axioms that make a simultaneous algebra and co-algebra into Hopf algebra is

Ï„:  HâŠ- H→HâŠ-H

Is the map Ï„(hâŠ-g)=gâŠ-h called the flip map ꓯ h, g ϵ H.”

Definition1.5

“Hopf Algebra is commutative if it’s commutative as algebra. It is co-commutative if it’s co-commutative as a co-algebra, τΔ=Δ. It can be defined as S²=id.

A commutative algebra over K is an algebra (A, m, η) over k such that m=m^op.”

Definition1.6

“Two Hopf algebras H,H^‘ are dually paired by a map < , > : H’ 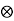H →k if,

<φψ, h> =<φ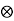ψ,Δh>, <1,h>=ε(h)

<Δφ, h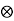g  >=<φ, hg>, ε(φ)=<φ,1>

=<φ, Sh>

ꓯ φ, ψϵ H’ and h, g ϵH.

Let (C, Δ,ε) be a co-algebra over k. The co-algebra (C, Δ^cop, ε) is the opposite co-algebra.

A co-commutative co-algebra over k is a co-algebra (C, Δ, ε) over k such that Δ= Δ^cop.”

Definition1.7

“A bi-algebra or Hopf algebra H acts on algebra A (called H-module algebra) if:

1. H acts on A as a vector space.
2. The product map m: A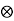A→A commutes with the action of H
3. The unit map η: k→ A commutes with the action of H.

From b,c we come to the next action

h⊳(ab)=∑(h(₁₎⊳a)(h₍₂₎⊳b), h⊳1= ε(h)1, ꓯa, b ϵ A, h ϵ H

This is the left action.”

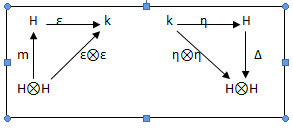
Definition1.8

“Let (A, m, η) be algebra over k and is a left H- module along with a linear map m: AâŠ-A→A and a scalar multiplication η: k âŠ- A→A if the following diagrams commute.”

Figure 3: Left Module map

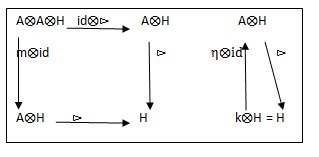
Definition1.9

“Co-algebra (C, Δ, ε) is H-module co-algebra if:

1. C is an H-module
2. Δ: C→C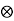C and ε: C→ k commutes with the action of H. (Is a right C- co-module).

Explicitly,

Δ(h⊳c)=∑h₍₁₎⊳c₍₁₎⨂h₍₂₎⊳c₍₂₎, ε(h⊳c)= ε(h)ε(c), ꓯh ϵ H, c ϵ C.”

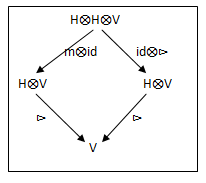
 Definition1.10

“A co-action of a co-algebra C on a vector space V is a map β: V→C⨂V such that,

1. (id⨂β) ∘β=(Δ⨂ id )β;
2.  id =(ε⨂id )∘β.”

Definition1.11

“A bi-algebra or Hopf algebra H co-acts on an algebra A (an H- co-module algebra) if:

1. A is an H- co-module
2. The co-action β: A→ H⨂A is an algebra homomorphism, where H⨂A has the tensor product algebra structure.”

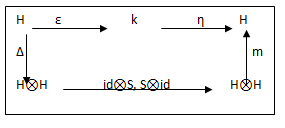
Definition1.12

“Let C be co- algebra (C, Δ, ε), map β: A→ H⨂A is a right C- co- module if the following diagrams commute.”

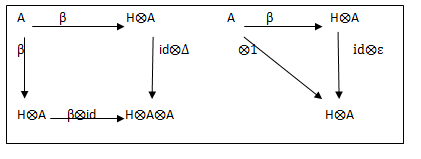
Figure 6:Co-algebra of a right co-module

“Sub-algebras, left ideals and right ideals of algebra have dual counter-parts in co-algebras. Let (A, m, η) be algebra over k and suppose that V is a left ideal of A. Then m(A⨂V)⊆V. Thus the restriction of m to A⨂V determines a map A⨂V→V. Left co-ideal of a co-algebra C is a subspace V of C such that the co-product Δ restricts to a map V→C⨂V.”

Definition1.13

“Let V be a subspace of a co-algebra C over k. Then V is a sub-co-algebra of C if Δ(V)⊆V⨂V, for left co-ideal Δ(V)⊆C⨂V and for right co-ideal Δ(V)⊆V⨂C.”

Definition1.14

“Let V be a subspace of a co-algebra C over k. The unique minimal sub-co-algebra of C which contains V is the sub-co-algebra of C generated by V.”

Definition1.15

“A simple co-algebra is a co-algebra which has two sub-co-algebras.”

Definition1.16

“Let C be co-algebra over k. A group-like element of C is c ϵC with satisfies, Δ(s)=s⨂s  and ε(s)=1 ꓯ s ϵS. The set of group-like elements of C is denoted G(C).”

Definition1.17

“Let S be a set. The co-algebra k[S] has a co-algebra structure determined by

Δ(s)=s⨂s  and ε(s)=1

ꓯ s ϵS. If S=∅ we set C=k[∅]=0.

Is the group-like co-algebra of S over k.”

Definition1.18

“The co-algebra C over k with basis {c_o, c₁, c₂,…..} whose co-product and co-unit is satisfy by Δ(c_n)= ∑c_n-l⨂c_l and ε(c_n)=δ_n,0 for l=1,….,n and for all n≥0. Is denoted by P_∞(k). The sub-co-algebra which is the span of c_o, c₁, c₂,…,c_n is denoted P_n(k).”

Definition1.19

“A co-matrix co-algebra over k is a co-algebra over k isomorphic to C_s(k) for some finite set S. The co-matrix identities are:

1. Δ(e_{i, j})= ∑e_{i, l}⨂e_{l, j}
2. ε(e_{i, j})=δ_{i, j}

∀ i, j ϵS. Set C_∅(k)=(0).”

Definition1.20

“Let S be a non-empty finite set. A standard basis for C_s(k) is a basis {c _{i ,j}}_{I, j ϵS} for C_s(k) which satisfies the co-matrix identities.”

Definition1.21

“Let (C, Δ_c, ε_c) and (D, Δ_D, ε_D) be co-algebras over the field k. A co-algebra map f: C→D is a linear map of underlying vector spaces such that Δ_D∘f=(f⨂f)∘ Δ_c and ε_D∘f= ε_c. An isomorphism of co-algebras is a co-algebra map which is a linear isomorphism.”

Definition1.22

“Let C be co-algebra over the field k. A co-ideal of C is a subspace I of C such that ε (I) = (0) and Δ (Ι) ⊆ I⨂C+C⨂I.”

Definition1.23

“The co-ideal Ker (ε) of a co-algebra C over k is denoted by C⁺.”

Definition1.24

“Let I be a co-ideal of co-algebra C over k. The unique co-algebra structure on C /I such that the projection Ï€: C→ C/I is a co-algebra map, is the quotient co-algebra structure on C/I.”

Definition1.25

“The tensor product of co-algebra has a natural co-algebra structure as the tensor product of vector space CâŠ-D is a co-algebra over k where Δ(c₍₁₎⨂d₍₁₎)⨂( c₍₂₎⨂d₍₂₎) and ε(c⨂d)=ε(c)ε(d) ∀ c in C and d in D.”

Definition1.26

“Let C be co-algebra over k. A skew-primitive element of C is a cϵC which satisfies Δ(c)= g⨂c +c⨂h, where c, h ϵG(c). The set of g:h-skew primitive elements of C is denoted  by

P_g,h (C).”

Definition1.27

“Let C be co-algebra over a field k. A co-commutative element of C is cϵC such that Δ(c) = Δ^cop(c). The set of co-commutative elements of C is denoted by Cc(C).

Cc(C) ⊆C.”

Definition1.28

“The category whose objects are co-algebras over k and whose morphisms are co-algebra maps under function composition is denoted by k-Coalg.”

Definition1.29

“The category whose objects are algebras over k and whose morphisms are co-algebra maps under function composition is denoted by k-Alg.”

Definition1.30

“Let (C, Δ, ε) be co-algebra over k. The algebra (C^âˆ-, m, η) where m= Δ^âˆ-| C^âˆ-⨂C^âˆ-, η (1) =ε, is the dual algebra of (C, Δ, ε).”

Definition1.31

“Let A be algebra over the field k. A locally finite A-module is an A-module M whose finitely generated sub-modules are finite-dimensional. The left and right C^âˆ--module actions on C are locally finite.”

Definition1.32

“Let A be algebra over the field k. A derivation of A is a linear endomorphism F of A such that F (ab) =F (a) b-aF(b) for all a, b ϵA.

For fixed b ϵA note that F: A→A defined by F(a)=[a, b]= ab- ba  for all a ϵA is a derivation of A.”

Definition1.33

“Let C be co-algebra over the field k. A co-derivation of C is a linear endomorphism f of C such that Δ∘f= (f⨂I_C + I_C ⨂f) ∘Δ.”

Definition1.34

“Let A and B ne algebra over the field k. The tensor product algebra structure on A⨂B is determined by (a⨂b)(a’⨂b’)= aa’⨂bb’ ꓯ a, a’ϵA and b, b’ϵB.”

Definition1.35

“Let X, Y be non-empty subsets of an algebra A over the field k. The centralizer of Y in X is

Z_X(Y) = {xϵX|yx=xy ꓯyϵY}

For y ϵA the centralizer of y in X is Z_X(y) = Z_X({y}).”

Definition1.36

“The centre of an algebra A over the field Z (A) = Z_A(A).”

Definition1.37

“Let (S, ≤) be a partially ordered set which is locally finite, meaning that ꓯ, I, jϵS which satisfy i≤j the interval [i, j] = {lϵS|i≤l≤j} is a finite set. Let S= {[i, j] |I, jϵS, i≤j} and let A be the algebra which is the vector space of functions f: S→k under point wise operations whose product is given by

(f⋆g)([i, j])=f([i, l])g([l, j])  i≤l≤j

For all f, g ϵA and [i, j]ϵS and whose unit is given by 1([I,j])= δ_i,j ꓯ[I,j]ϵS.”

Definition1.38

“The algebra of A over the k described above is the incidence algebra of the locally finite partially ordered set (S, ≤).”

Definition1.39

“Lie co-algebra over k is a pair (C, δ), where C is a vector space over k and δ: C→C⨂C is a linear map, which satisfies:

τ∘δ=0 and (Ι+(τ⨂Ι)∘(Ι⨂τ)+(Ι⨂τ)∘ (τ⨂Ι))∘(Ι⨂δ)∘δ=0

Ï„=Ï„_C,C and I is the appropriate identity map.”

Definition1.40

“Suppose that C is co-algebra over the field k. The wedge product of subspaces U and V is U∧V = Δ^-1(U⨂C+ C⨂V).”

Definition1.41

“Let C be co-algebra over the field k. A saturated sub-co-algebra of C is a sub-co-algebra D of C such that U∧V⊆D, ꓯ U, V of D.”

Definition1.42

“Let C be co-algebra over k and (N, ρ) be a left co-module. Then U∧X= ρ^-1(U⨂N+ C⨂X) is the wedge product of subspaces U of C and X of N.”

Definition1.43

“Let C be co-algebra over k and U be a subspace of C. The unique minimal saturated sub-co-algebra of C containing U is the saturated closure of U in C.”

Definition1.44

“Let (A, m, η) be algebra over k. Then,

1. A^∘=m^∖1(A^âˆ-⨂A^âˆ- )
2. (A^∘, Δ, ε) is a co-algebra over k, where Δ= m^âˆ-| A^∘ and ε=η^âˆ-.

Τhe co-algebra (A^∘, Δ, ε) is the dual co-algebra of (A, m, η).

Also we denote A^∘ by a^∘ and Δ^∘= a^∘₍₁₎⨂ a^∘₍₂₎, ꓯ a^∘ ϵ A^∘.”

Definition1.45

“Let A be algebra over k. An η:ξ- derivation of A is a linear map f: A→k which satisfies f(ab)= η(a)f(b)+f(a) ξ(b), ꓯ a, bϵ A and η, ξ ϵ Alg(A, k).”

Definition1.46

“The full subcategory of k-Alg (respectively of k-Co-alg) whose objects are finite dimensional algebras (respectively co-algebras) over k is denoted k-Alg _fd (respectively     k-Co-alg _fd).”

Definition1.47

“A proper algebra over k is an algebra over k such that the intersection of the co-finite ideals of A is (0), or equivalently the algebra map j_A:A→(A^∘)*, be linear map defined by j_A(a)(a^∘)=a^∘(a), a ϵA and a^∘ϵA^∘. Then:

1. j_A:A→(A^∘)* is an algebra map
2. Ker(j_A) is the intersection of the co-finite ideals of A
3. Im(j_A) is a dense subspace of (A^∘)*.

Is one-to-one.”

Definition1.48

“Let A (respectively C) be an algebra (respectively co-algebra ) over k. Then A (respectively C) is reflexive if j_A:A→(A^∘)*, as defined before and j_C:C→(C*)^∘, defined as:

j_C(c)(c^*)=c^*(c), ꓯ c*ϵC* and cϵC. Then:

1. Im(j_C)⊆(C*)^∘ and j_C:C→(C*)^∘ is a co-algebra map.
2. j_C is one-to-one.
3. Im(j_C) is the set of all aϵ(C*)* which vanish on a closed co-finite ideal of C*.

Is an isomorphism.”

Definition1.49

“Almost left noetherian algebra over k is an algebra over k whose co-finite left ideal are finitely generated. (M is called almost noetherian if every co-finite submodule of M is finitely generated).”

Definition1.50

“Let f:U→V be a map of vector spaces over k. Then f is an almost one-to-one linear map if ker(f) is finite-dimensional, f is an almost onto linear map if Im(f) is co-finite subspace of V and f is an almost isomorphism if f is an almost one-to-one and an almost linear map.”

Definition1.51

“Let A be algebra over k and C be co-algebra over k. A pairing of A and C is a bilinear map

 β: AÃ-C→k which satisfies, β(ab,c)= β (a, c₍₁₎)β (b, c₍₂₎) and β(1, c) = ε(c), ꓯ a, b ϵ A and        c ϵC.”

Definition1.52

“Let V be a vector space over k. A co-free co-algebra on V is a pair (Ï€, T^co(V)) such that:

1. T^co(V) is a co-algebra over k and π: T^co(V)→T is a linear map.
2. If C is a co-algebra over k and f:C→V is a linear map,∃ a co-algebra map F: C→ T^co(V) determined by π∘F=f.”

Definition1.53

“Let V be a vector space over k. A co-free co-commutative co-algebra on V is any pair (Ï€, C(V)) which satisfies:

1. C(V) is a co-commutative co-algebra over k and π:C(V)→V is a linear map.
2. If C is a co-commutative co-algebra over k and f: C→V is linear map, ∃ co-algebra map F:C →C(V) determined by π∘F=f. “                  (Majid 2002, Radford David E)

Chapter 2

Proposition (Anti-homomorphism property of antipodes) 2.1

“The antipode of a Hopf algebra is unique and obey S(hg)=S(g)S(h), S(1)=1 and (S⨂S)∘Δh=τ∘Δ∘Sh, εSh=εh, ∀h,g ∈ H. “             (Majid 2002, Radford David E)

Proof

Let S and S₁ be two antipodes for H. Then using properties of antipode, associativity of Ï„ and co-associativity of Δ we get

S= τ∘(SâŠ-[ τ∘(IdâŠ-S₁)∘Δ])∘Δ= τ∘(IdâŠ- Ï„)∘(S⨂IdâŠ-S₁)∘(Id âŠ-Δ)∘Δ=

τ∘(τ⨂Id)∘(S⨂IdâŠ-S₁)∘(Δ âŠ-Id)∘Δ = τ∘( [τ∘(S⨂Id)∘Δ]⨂S₁)∘ Δ=S₁.

So the antipode is unique.

Let Sâˆ-id=ε_s idâˆ-S=ε_t

To check that S is an algebra anti-homomorphism, we compute

S(1)= S(1₍₁₎)1₍₂₎S(1₍₃₎)= S(1₍₁₎) ε_t (1₍₂₎)= ε_s(1)=1,

S(hg)=S(h₍₁₎g₍₁₎) ε_t(h₍₂₎g₍₂₎)= S(h₍₁₎g₍₁₎)h₍₂₎ ε_t(g₍₂₎)S(h₍₃₎)=ε_s (h₍₁₎g₍₁₎)S(g₍₂₎)S(h₍₂₎)=

S(g₍₁₎) ε_s(h₍₁₎) ε_t (g₍₂₎)S(h₍₂₎)=S(g)S(h), ∀h,g ∈H and we used ε_t(hg)= ε_t(h ε_t(g)) and ε_s(hg)= ε_t(ε_s(h)g).

Dualizing the above we can show that S is also a co-algebra anti-homomorphism:

ε(S(h))= ε(S(h₍₁₎ ε_t(h₍₂₎))= ε(S(h₍₁₎h₍₂₎)= ε(ε_t(h))= ε(h),

Δ(S(h))= Δ(S(h₍₁₎ ε_t(h₍₂₎))= Δ(S(h₍₁₎ ε_t(h₍₂₎)⨂1)= Δ(S(h₍₁₎ ))(h₍₂₎S(h₍₄₎)⨂ ε_t (h₍₃₎)=

Δ(ε_s(h₍₁₎)(S(h₍₃₎)⨂S(h₍₂₎))=S(h₍₃₎)⨂ ε_s(h₍₁₎)S(h₍₂₎)=S(h₍₂₎)⨂ S(h₍₁₎). (New directions)

Example2.2

“The Hopf Algebra H=U_q(b₊) is generated by 1 and the elements X,g,g^-1 with relations

gg^-1=1=g^-1g and g X=q X g, where q  is a fixed invertible element of the field k. Here

ΔX= X⨂1 +g ⨂ X, Δg=g ⨂ g, Δg^-1=g^-1⨂g^-1,

εX=0, εg=1=ε g^-1, SX=- g^-1X, Sg= g^-1, S g^-1=g.

S²X=q^-1X.”

Proof

We have Δ, ε on the generators and extended them multiplicatively to products of the generators.

ΔgX=(Δg)( ΔX)=( g⨂g)( X⨂1 +gâ