Euler's Totient Theorem

Summary   

Euler Totient theorem is a generalized form of Fermat’s Little theory. As such, it solely depends on Fermat’s Little Theorem as indicated in Euler’s study in 1763 and, later in 1883, the theorem was named after him by J. J. Sylvester. According to Sylvester, the theorem is basically about the alteration in similarity. The term “Totient” was derived from “Quotient”, hence, the function deals with division, but in a unique way. In this manner, The Euler’s Totient function φ for any integer (n) can be demarcated, as the figure of positive integers is not greater than and co-prime to n.

a^φ(n) = 1 (mod n)

Based on Leonhard Euler’s contributions toward the development of this theorem, the theory was named after him despite the fact that it was a generalization of Fermat’s Little Theory in which n is identified to be prime. Based on this fact, some scholarly source refers to this theorem as the Fermat’s-Euler theorem of Euler’s generalization.

Introduction

I first developed an interest in Euler when I was completing a listener crossword; the concealed message read “Euler was the master of the crossword.” When I first saw the inclusion of the name “Euler” on the list of prompt words, I had no option but to just go for it. Euler was a famous mathematician in the eighteenth century, who was acknowledged for his contribution in the mathematics discipline, as he was responsible for proving numerous problems and conjectures. Taking the number theory as an example, Euler successively played a vital role in proving the two-square theorem as well as the Fermat’s little theorem (Griffiths and Peter 81). His contribution also paved the way to proving the four-square theorem. Therefore, in this course project, I am going to focus on his theory, which is not known to many; it is a generalization of Fermat’s little theorem that is commonly known as Euler’s theorem.

Theorem

Euler’s Totient theorem holds that if a and n are coprime positive integers, then 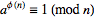since Φ_n is a Euler’s Totient function.

Euler’s Totient Function

Euler’s Totient Function (Φ_n) is the count of positive integers that are less that n and relatively prime to n. For instance, Φ₁₀ is 4, since there are four integers, which are less than 10 and are relatively prime to 10: 1, 3, 7, 9. Consequently, Φ₁₁ is 10, since there 11 prime numbers which are less than 10 and are relatively prime to 10. The same way, Φ₆ is 2 as 1 and 5 are relatively prime to 6, but 2, 3, and 4 are not.

The following table represents the totients of numbers up to twenty.

Some of these examples seek to prove Euler’s totient theorem.

Let n = 10 and a = 3. In this case, 10 and 3 are co-prime i.e. relatively prime. Using the provided table, it is clear that Φ10 = 4. Then this relation can also be represented as follows:

3⁴ = 81 ≡ 1 (mode 10). Conversely, if n = 15 and a = 2, it is clear that 2⁸ = 256 ≡ 1 (mod 15).

Fermat’s Little Theory

According to Liskov (221), Euler’s Totient theorem is a simplification of Fermat’s little theorem and works with every n that are relatively prime to a. Fermat’s little theorem only works for a and p that are relatively prime.

a ^p-1 ≡ 1 (mod p)

or

a ^p ≡ a (mod p)

where p itself is prime.

It is, therefore, clear that this equation fits in the Euler’s Totient theorem for every prime p, as indicated in Φ_p, where p is a prime and is given by p-1.

Therefore, to prove Euler’s theorem, it is vital to first prove Fermat’s little theorem.

Proof to Fermat’s Little Theorem

As earlier indicated, the Fermat’s little theorem can be expressed as follows:

a^p ≡ a (mod p)

taking two numbers: a and p, that are relatively prime, where p is also prime.

The set of a {a, 2a, 3a, 4a, 5a…(p-1)a}………(i)

Consider another set of number {1, 2, 3, 4, 5….(p-1a)}……(ii)

If one decides to take the modulus for p, each element of the set (i) will be congruent to an item in the second set (ii). Therefore, there will be one on one correspondence between the two sets. This can be proven as lemma 1.

Consequently, if one decides to take the product of the first set, that is {a x 2a x 3a x 4a x 5a x …. (p-1)a } as well as the product of the second set as {1 x 2 x 3 x 4 x 5… (p-1)}. It is clear that both of these sets are congruent to one another; that is, each element in the first set matches another element in the second set (Liskov 221).

Therefore, the two sets can be represented as follows:

{a x 2a x 3a x 4a x 5a x …. (p-1)a } ≡ {1 x 2 x 3 x 4 x 5… (p-1)} (mode p).

If one takes out the factor a ^p-1 from the left-hand side (L.H.S), the resultant equation will be A^p-1 {a x 2a x 3a x 4a x 5a x …. (p-1)a } ≡ {1 x 2 x 3 x 4 x 5… (p-1)} (mode p).

If the same equation is divided by {1 x 2 x 3 x 4 x 5… (p-1)} when p is prime, one will obtain

a ^p ≡ a (mod p)

or

a ^p-1 ≡ 1 (mod p)

It should be clear that each element in the first set should correspond to another element in the second set (elements of the set are congruent). Even though this is not obvious at the first step, it can still be proved through three logical steps as follows:

1. Each element in the first set should be congruent to one element in the second set; this implies that none of the elements will be congruent to 0, as pand a are relatively prime.
2. No two numbers in the first set can be labeled as ba or ca. If this is done, some elements in the first set can be the same as those in the second set. This would imply that two numbers are congruent to each other i.e. ba ≡ ca (mod p), which would mean that b ≡ c (mod p) which is not true mathematically, since both the element are divergent and less than p.
3. An element in the first set can not be congruent to two numbers in the second set, since a number can only be congruent to numbers that differ by multiple of p.

Through these three rules, one can prove Fermat’s Little Theorem.

Proof of Euler’s Totient Theorem

Since the Fermat’s little theorem is a special form of Euler’s Totient theorem, it follows that the two proofs provided earlier in this exploration are similar, but slight adjustments need to be made to Fermat’s little theorem to justify Euler’s Totient theorem (KrÌŒízÌŒek 97). This can be done by using the equation

a ^Φn ≡ 1 (mod n)

where the two numbers, a and n, are relatively prime, with the set of figures N, which are relatively prime to n {1, n₁. n₂….n _Φn }. This set is likely to have Φn element, which is defined by the number of the relatively prime number to n. In the same way, in the second set aN, each and every element is a product of a as well as an element of N {a, an₁, an₂, an₃…an_Φn}.

Each element of the set aN must be congruent to another element in the set N (mode n) as noted by the earlier three rules. Therefore, each element of the two sets will be congruent to each other (Giblin 111).

In this scenario case, it can be said that:

{a x an₁ x an₂ x an₃ x …. an _Φn } ≡ {a x  n₁ x n₂ x n₃ x ….n _Φn } (mod n).

By factoring out a and a^Φn from the left-hand side, one can obtain the following equation

a ^Φn {1 x n₁ x n₂ x n₃ x ….n _Φn} ≡ {1 x n₁ x n₂ x n₃ x ….n _Φn } (mod n)

If this obtained equation is divided by {1 x n₁ x n₂ x n₃ x ….n _Φn } from both sides, all the elements in the two sets will be relatively prime. The obtained equation will be as follows:

a ^Φn ≡ 1 (mod n)

Application of the Euler’s Theorem

Unlike other Euler’s works in the number theory like the proof for the two-square theorem and the four-square theorem, the Euler’s totient theorem has real applications across the globe. The Euler’s totient theorem and Fermat’s little theorem are commonly used in decryption and encryption of data, especially in the RSA encryption systems, which protection resolves around big prime numbers (Wardlaw 97).

Conclusion

In summary, this theorem may not be Euler’s most well-designed piece of mathematics; my favorite theorem is the two-square theorem by infinite descent. Despite this, the theorem seems to be a crucial and important piece of work, especially for that time. The number theory is still regarded as the most useful theory in mathematics nowadays. Through this proof, I have had the opportunity to connect some of the work I have earlier done in discrete mathematics as well as sets relation and group options. Indeed, these two options seem to be among the purest sections of mathematics that I have ever studied in mathematics. However, this exploration has enabled me to explore the relationship between Euler’s totient theorem and Fermat’s little theorem. I have also applied knowledge from one discipline to the other which has broadened my view of mathematics.

Works Cited