Derivation and Geometry of the Catenary Curve

Mathematics SL

Derivation and Geometry of the Catenary Curve

Table of Contents

Introduction —————————————————

My biggest interest has always been art and design. Both my brother and my dad work in construction which introduced me to architecture as a possible field of study. Since grade 9 I knew I wanted to be an architect, and so when I researched my IA topic I was looking for something related to that field. The catenary curve caught my attention when I was looking at the St. Louis Gateway Arch, a tourist attraction I have visited many times before. I always assumed it was a parabolic arch but the shape is actually a catenary[1]. Most structures use a catenary arch as opposed to a parabolic arch because it able to withstand both its own weight and additional loads. The shape of a catenary allows for the weight to be directed along the curve to the supports at the base of the arch.[2] In this IA, I will be explaining the geometry of the catenary curve as well as deriving its equation.

[3]

St.Louis Gateway Arch designed by architect Eero Saarinen

The Catenary Curve ——————————————

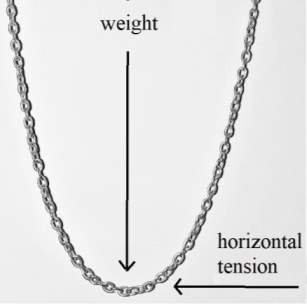
The catenary curve is naturally formed by a hanging chain or cable with only the force of gravity acting upon it.[4] The uniform gravitational force causes the center of the chain to dip, forming a curve symmetrical on either side of the minimum point.

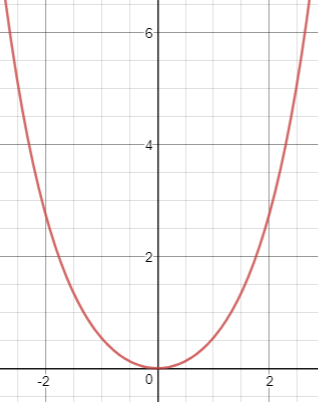
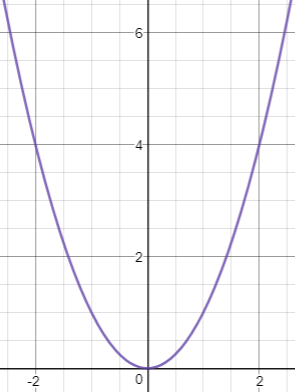
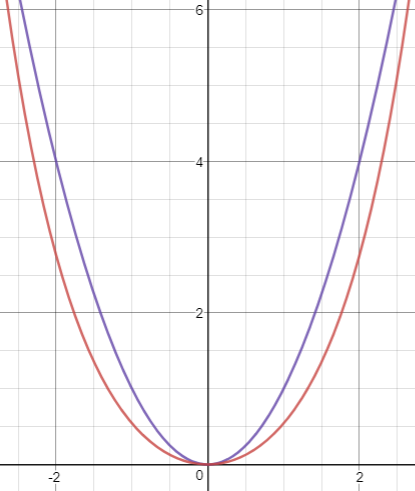
Galileo Galilei, famous astronomer and mathematician, claimed that the curve of a hanging chain is simply a parabola. Leibniz, Huygens and Johann Bernoulli found the equation of the catenary curve in 1690[5], finding that it is not a parabola but a hyperbolic cosine.[6]

Equation of the catenary curve[7]:

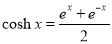or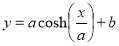 

where;

          y is the ordinate of any point on the curve

          x is the abscissa of any point on the curve

          e is Euler’s number or,

          a is a constant: horizontal tension divided by the weight per unit length (of the chain)*

          b is the constant of integration, affecting the y-intercept of a graphed catenary curve*

*will be explained further

This equation was derived using simple vector equation, trigonometric identities, and calculus.

Geometry and Defining Variables —————————

The geometry of the Catenary is, at its root, a physics problem. Two common equations are used; the force acting on an object, and the weight of an object.

Force acting on an object[8]:

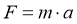
where;

          F is force

          m is mass of the object

          a is the acceleration of the object

The weight of an object is the force of its mass as it is accelerated due to gravity.Therefore;

Weight of an object:

where;

          W is the weight of the object

          m is mass of the object

          g is the acceleration due to gravity

This is a vector quantity, as gravity pulls downwards on the mass of an object with a magnitude equal to its weight ().

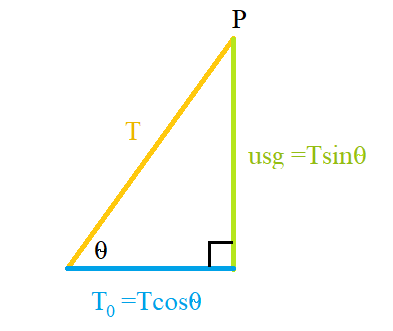
The horizontal vector quantity is the horizontal tension, which is the same for each point on the curve because the only force acting on the chain is gravity (a vertical force). Hence, the magnitude of the horizontal tension vector for every point on the curve will be equal.

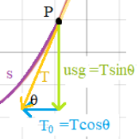
Before deriving the equation, it is important to define the variable used; all variables are illustrated in the following diagram[9]:

where;

          A is the lowest point on the curve

          P is an arbitrary point on the curve

          T is the tangent of ‘P’

          s is the length of the curve from point ‘A’ to point ‘P’

          u is the mass per unit length

Further definitions:

The mass of the curve supported by point ‘P’ is given by 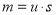(mass per unit length multiplied by the length). The weight is therefore 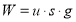which is the vertical force acting on each point of the curve.

To prove the relation between each component;

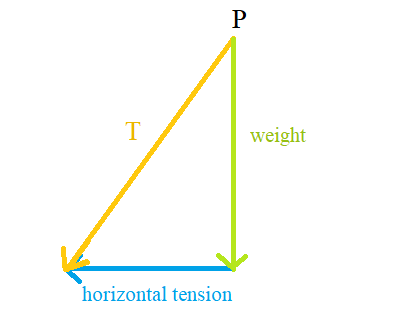
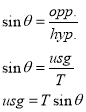
Tangent ‘T’ is also the resultant vector of adding the vertical (W) and horizontal tension (H) vectors.

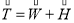
It is sometimes referred to as tangential tension or tangential force.

By the Pythagorean Theorem, the relation between all three components is:

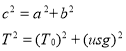
An equation necessary for the derivation of the catenary curve is the tangent of theta; which is the relation between the two known constants (the weight an the horizontal tension). 

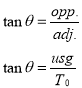
The variable ‘s’ is the only part of this equation that is unknown to the arbitrary (does not matter, as long as it is on the curve) point ‘P’. To simplify the equation, the constant ‘a’ is defined and does not contain ‘s’. Using the equation for the tangent of theta and the new constant, the intrinsic equation (relating intrinsic properties of the curve) of the catenary can be found. The intrinsic equation defines the curve without considering the location of the curve itself.[10]

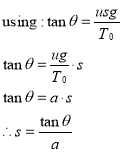
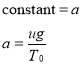
Derivation ————————————————————

Using all of the above information as formulas, the equation of the catenary curve is derived.

The slope of any given point on this curve is given by;

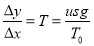
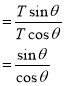
According to the trigonometric identity;

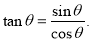
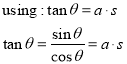
The tangent at any point on the graph is T, now know as the tangent of angle theta. This allows us to conclude that;

However, we want the equation to be written in rectangular coordinates (x,y) so that there are only 2 variables. The variable ‘s’ prevents the equation from being expressed in terms of x and y (a is a constant). This would mean that someone has to know the length of the chain in order to use this equation. To eliminate the variable ‘s’, both side are differentiated.

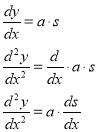
The differential of arc length (applicable to length of a curve) is given by the equation[11];

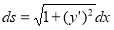
By substitution, it is found that;

This is the simplified equation of the substituted variable ‘s’. Finding the integral is the reverse of finding a derivative, and so integrating both side solves the differential equation that will allow the curve to be expressed in terms of x and y.

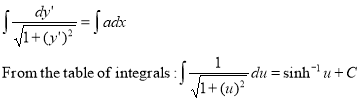
where;

          u is a variable

          C is the unknown constant of integration

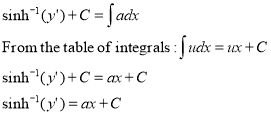
*An unknown constant subtracted by an unknown constant is an unknown constant.

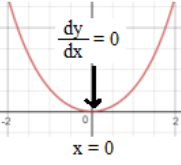
When x is equal to 0, as the catenary curve is center along the y-axis, then that slope at that point is 0. This results in the unknown constant ‘C’ canceling out.

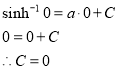
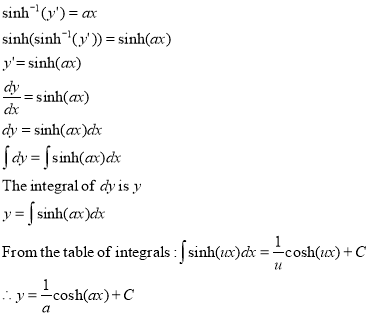
The constant ‘a’ that was set as 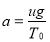can also be its inverse. If then the equation can be rewritten as:

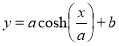
where;

          y is the ordinate of any point on the curve

          x is the abscissa of any point on the curve

          a determines the slope of the catenary (the weight of any point on the chain, when speaking about catenary, divided by the horizontal tension )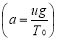

          b determines the y-intercept (the unknown constant of integration)

Application————————————————————

The inverted catenary curve forms an arch that can support itself.[12] This is because, as the shape of a hanging chain, there is already a balance between the horizontal tension (from the supports) and the weight of the chain. The curve has equal forces acting vertically and horizontally. A structure built using the catenary arch is therefore structurally stable without the need for beams or columns.

The famous Spanish architect Antoni Gaudí had used catenary arches in many of his projects. His designs were used to construct churches, houses, outdoor structures, and many more famous works of art in Barcelona and Spain.[13]

Park Güell in Barcelona, Spain designed by Antoni Gaudí

Gaudí is now my favourite architect and an excellent example of the catenary arch’s versatility, but I would like to bring the discussion back to the St. Louis Gateway Arch. The arch is 190.5 meters tall and spans a distance of 182.3 meters.[14] We can scale that down to 1.905 cm in height and 1.823 cm span. Using desmos and the equation derived in the previous section;

It is found that the equation of an arch proportionate to the the St. Louis Gateway arch is;

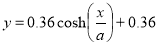
This does not not show a direction relation between the height and span of an arch and the equation, but it allows us to see the shape of a catenary arch in mathematical terms. It is clear that the hyperbolic cosine is the true shape of a catenary arch. Using this knowledge the construction of arches can be done more accurately.

Conclusion ———————————————————

The structural properties of the curve are unique and ideal for the construction of an arch. For hundreds of years this poor curve was mistaken for a parabola. In light of Leibniz, Huygens and Johann Bernoulli’s discovery, it is now know to be a hyperbolic cosine. The catenary curve is derived from the shape of a hanging chain using trigonometry, a little bit of vectors, and calculus. What was once a physics problem is now my favourite math problem.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

The derivation of the catenary curve allowed me to apply my knowledge of trigonometry and calculus to a topic that I am interested in. The catenary arch, modeled by the hyperbolic cosine, could one day be incorporated into my architectural designs.

Bibliography ———————————————————

• (n.d.). Retrieved from http://makingmathvisible.com/catenary/catenary.html
• Britannica, T. E. (2017, September 14). Force. Retrieved December 15, 2018, from https://www.britannica.com/science/force-physics
• Calter, P. (n.d.). Gateway to Mathematics Equations of the St. Louis Arch. Retrieved January 2, 2019, from https://link.springer.com/content/pdf/10.1007/s00004-006-0017-7.pdf
• Carlisle, A. (2013, November 17). Catenary Equation Derivation. Retrieved December 15, 2018, from https://youtu.be/P-2lqcaFvUE
• Carlson, S. C. (2017, February 03). Catenary. Retrieved January 2, 2019, from https://www.britannica.com/science/catenary
• Catenary. (1997, January 1). Retrieved January 2, 2019, from http://www-history.mcs.st-andrews.ac.uk/Curves/Catenary.html
• Huerta, S. (2006, May 20). Structural Design in the Work of Gaudi. Retrieved January 2, 2019, from http://oa.upm.es/703/1/Huerta_Art_002.pdf
• Kaplan, G. (n.d.). The Catenary Art, Architecture, History, and Mathematics. Retrieved January 1, 2019, from http://archive.bridgesmathart.org/2008/bridges2008-47.pdf
• Kouba, D. (Ed.). (2017, May 3). COMPUTING THE ARC LENGTH OF A DIFFERENTIABLE FUNCTION ON A CLOSED INTERVAL. Retrieved December 21, 2018, from https://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/arclengthdirectory/ArcLength.html
• Person. (2016, October 28). Share your story: Happy birthday, Gateway Arch! Retrieved January 1, 2019, from https://www.ksdk.com/article/news/local/share-your-story-happy-birthday-gateway-arch/63-343653644
• Porter, N. (Ed.). (n.d.). Intrinsic equation of a curve. Retrieved December 16, 2018, from https://www.webster-dictionary.org/definition/Intrinsic equation of a curve
• Revolvy, L. (Ed.). (n.d.). “Catenary arch” on Revolvy.com. Retrieved January 1, 2019, from https://www.revolvy.com/page/Catenary-arch
• Weisstein, E. (2019, January 9). Catenary. Retrieved January 11, 2019, from http://mathworld.wolfram.com/Catenary.html

[1] (n.d.). Retrieved from http://makingmathvisible.com/catenary/catenary.html

[2] Revolvy, L. (Ed.). (n.d.). “Catenary arch” on Revolvy.com. Retrieved January 1, 2019, from https://www.revolvy.com/page/Catenary-arch

[3] Person. (2016, October 28). Share your story: Happy birthday, Gateway Arch! Retrieved January 1, 2019, from https://www.ksdk.com/article/news/local/share-your-story-happy-birthday-gateway-arch/63-343653644

[4] Weisstein, E. (2019, January 9). Catenary. Retrieved January 11, 2019, from http://mathworld.wolfram.com/Catenary.html

[5] Catenary. (1997, January 1). Retrieved January 2, 2019, from http://www-history.mcs.st-andrews.ac.uk/Curves/Catenary.html

[6] Carlson, S. C. (2017, February 03). Catenary. Retrieved January 2, 2019, from https://www.britannica.com/science/catenary

[7] Carlisle, A. (2013, November 17). Catenary Equation Derivation. Retrieved December 15, 2018, from https://youtu.be/P-2lqcaFvUE

[8] Britannica, T. E. (2017, September 14). Force. Retrieved December 15, 2018, from https://www.britannica.com/science/force-physics

[9] Carlisle, A. (2013, November 17). Catenary Equation Derivation. Retrieved December 15, 2018, from https://youtu.be/P-2lqcaFvUE

[10] Porter, N. (Ed.). (n.d.). Intrinsic equation of a curve. Retrieved December 16, 2018, from https://www.webster-dictionary.org/definition/Intrinsic equation of a curve

[11] Kouba, D. (Ed.). (2017, May 3). COMPUTING THE ARC LENGTH OF A DIFFERENTIABLE FUNCTION ON A CLOSED INTERVAL. Retrieved December 21, 2018, from https://www.math.ucdavis.edu/~kouba/CalcTwoDIRECTORY/arclengthdirectory/ArcLength.html

[12] Kaplan, G. (n.d.). The Catenary Art, Architecture, History, and Mathematics. Retrieved January 1, 2019, from http://archive.bridgesmathart.org/2008/bridges2008-47.pdf

[13] Huerta, S. (2006, May 20). Structural Design in the Work of Gaudi. Retrieved January 2, 2019, from http://oa.upm.es/703/1/Huerta_Art_002.pdf

[14] Calter, P. (n.d.). Gateway to Mathematics Equations of the St. Louis Arch. Retrieved January 2, 2019, from https://link.springer.com/content/pdf/10.1007/s00004-006-0017-7.pdf