Strain Gauge Laboratory Exercise
| ✅ Paper Type: Free Essay | ✅ Subject: Engineering |
| ✅ Wordcount: 2618 words | ✅ Published: 31 Aug 2017 |
An investigation into the effects of electronic circuits on the accuracy of weight measurement and how these results relate to material properties
Instrumentation systems are necessary in industry to provide accurate and reliable measurements of various quantities, as well as monitoring and controlling processes. In this experiment, strain gauge sensors were attached to a cantilever beam upon which a varying load was applied and the output voltage recorded in order to estimate the mass of an unknown object. This was done for four separate electrical circuits, involving potential dividers and Wheatstone bridges, to compare their respective accuracies in measuring the unknown mass. The obtained results were also used to calculate an estimate for the Young’s Modulus of the steel beam, which was found to be 46.6 GPa. This differed greatly from the expected value of 200 GPa due to the irregular thickness of the beam, which affected the calculated results for the stress and highlighted the need to reduce sources of error before and during experiments.
An instrumentation system is ‘a collection of instruments used to measure, monitor and control a process.’ (1) These systems are regularly used for a variety of measurements in industries including communications, defence and engineering systems. The instrumentation systems involved in these measurement processes usually comprise of a sensor and appropriate electronic circuitry to manipulate and process the signal. Utilisation of these systems in industry is rapidly increasing as they continue to increase productivity and quality through the reduction of human error in the measurements made.
The strain gauge is one of the most important sensors regarding the measurement of mechanical quantities. A strain gauge is ‘a sensor whose resistance varies with applied force.’ (2) The variation in length produced by the force causes a change in electrical resistivity across the gauge which can be measured and used to calculate values of stress and strain. This report investigates the effects of different electronic circuits on the accuracy of weight measurement using strain gauge sensors on a cantilever beam and a comparison between experimental and theoretical results for Young’s Modulus.
The different circuits considered are:
- a potential divider circuit
- a Wheatstone bridge circuit in quarter bridge configuration
- a Wheatstone bridge circuit in half bridge configuration
- a Wheatstone bridge and amplifier circuit
A cantilever beam is a beam anchored only at one end, as shown in figure 1 below.
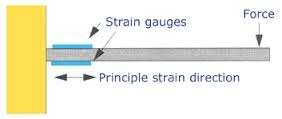


As stated in the introduction, the application of a force on the beam alters its length which subsequently changes the strain gauge resistance. This change in resistance is given by:
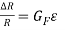 (equation 1)
(equation 1)
where R is the resistance of the gauge, ∆R is the change in resistance, 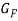 is the gauge factor (which is 2 throughout this experiment) and ε is the strain.
is the gauge factor (which is 2 throughout this experiment) and ε is the strain.
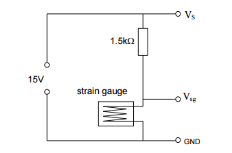 In the potential divider set up illustrated below in figure 2, the 1.5kΩ resistor is in series with the strain gauge and, as the resistance across the strain gauge varies with the load applied, the voltage across the strain gauge will also change. This voltage can be measured and used to calculate the strain on the beam.
In the potential divider set up illustrated below in figure 2, the 1.5kΩ resistor is in series with the strain gauge and, as the resistance across the strain gauge varies with the load applied, the voltage across the strain gauge will also change. This voltage can be measured and used to calculate the strain on the beam.

Deformation to the strain gauge through the applied force generates a very small change in resistance, causing only a very small change in voltage for the masses added. For this reason, it is more accurate to measure the change in voltage instead of the overall output voltage. This can be achieved through the use of a circuit known as a Wheatstone bridge. A Wheatstone bridge contains ‘two simple series-parallel arrangements of resistances connected between a voltage supply terminal and ground producing zero voltage difference between the two parallel branches when balanced.’ (3) The arrangement of this is shown in figure 3 below:
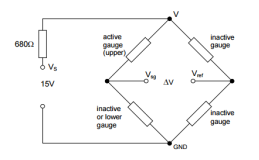

For this investigation, the bridge is arranged in two different configurations, quarter bridge and half bridge, changing the number of arms made active.
The bridge is originally balanced so the resistances in the lower and upper arms of each adjacent sides are equal, giving a 0V output. Therefore, a change in resistance of one of the active arms as the beam deforms gives rise to a voltage output ∆V which can be measured through equation 2:
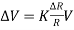 (equation 2)
(equation 2)
where V is the bridge excitation voltage, R is the gauge resistance, ∆R is the change in resistance and K =  for a quarter bridge set up and
for a quarter bridge set up and  for a half bridge set up.
for a half bridge set up.
Equation 1 and equation 2 can then be combined to produce an equation for calculating the induced stress in the material:
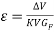 (equation 3)
(equation 3)
When a load W is applied to the beam, the stress at the strain gauge at distance L is given by the equation:
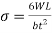 (equation 4)
(equation 4)
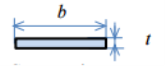 where σ is the surface stress, W is the applied force, L is the distance between the load and the strain gauge sensors, b is the width of the beam and t is the thickness of the beam (see figure 4).
where σ is the surface stress, W is the applied force, L is the distance between the load and the strain gauge sensors, b is the width of the beam and t is the thickness of the beam (see figure 4).

Young’s modulus can then be calculated through Hooke’s Law:
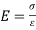 (equation 5)
(equation 5)
4.1 Apparatus
The experiment was conducted using the apparatus illustrated in figure 5, as well as utilising measuring equipment described below:
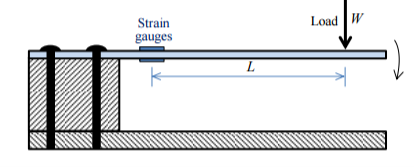

Cantilever beam set up as shown in figure 5, with a pair of 120kΩ strain gauges attached at a distance from the free end, one above the beam and one below.
Cantilever beam casing containing 2 switches to alternate between the potential divider and Wheatstone bridge circuits and then, for the latter, between quarter bridge and half bridge configuration.
Masses, 100g each, to vary the load applied to the free end.
Circuit board with potential divider, Wheatstone bridge and amplifier circuits set up containing potentiometers and pins to allow voltage to be measured across components.
Digital Multimeter to record the output voltages of the circuit, measuring with an uncertainty of ±0.5mV for the potential divider and ±0.05mV for the Wheatstone bridges.
Vernier caliper to measure the width and thickness of the beam, as well as the distance from the strain gauges to the load, measuring with an uncertainty of ±0.005cm.
Digital scales to calculate the actual mass of the unknown object, measuring with an accuracy of ±0.05g.
4.2 Procedure
The first electric circuit to be tested was the potential divider and therefore the switch on the cantilever beam casing was set to the corresponding place. With no load applied, the voltage across the strain gauge,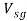 , was measured. The minimum weight, 100g, was then loaded onto the beam and both the total weight and voltage across the strain gauge,
, was measured. The minimum weight, 100g, was then loaded onto the beam and both the total weight and voltage across the strain gauge, 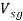 , were recorded. The weight was then increased in 100g increments up to a maximum of 500g with the total weight and
, were recorded. The weight was then increased in 100g increments up to a maximum of 500g with the total weight and 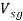 recorded after each mass was added. Finally, the load was removed and replaced with an unknown weight for which the voltage reading was recorded.
recorded after each mass was added. Finally, the load was removed and replaced with an unknown weight for which the voltage reading was recorded.
The first switch was then changed to select the Wheatstone bridge circuit, and the second switch to choose the quarter bridge configuration. With no load applied to the beam, the excitation voltage, V, for the bridge was then measured and recorded. This circuit contained a potentiometer which was then altered to change the resistance and ensure the initial output read 0V on the multimeter. The same procedure as for the potential divider was then carried out and the results recorded for the same differentials.
The second switch was then changed to select the half bridge configuration and an identical procedure to the quarter bridge was carried out.
The second switch was then changed back to the quarter bridge configuration while the circuit was changed to include a differential amplifier to increase the output voltage. The circuit is shown in figure 5 below:
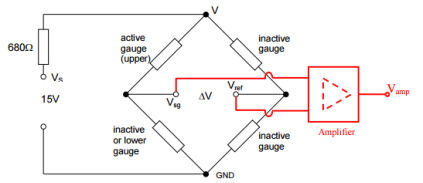

The same method was then followed as used for the previous Wheatstone bridge without the amplifier; however, this time, the amplified voltage 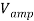 was measured and recorded as opposed to the actual output voltage
was measured and recorded as opposed to the actual output voltage 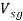 .
.
Finally, after all the necessary measurements using the equipment were recorded, the unknown weight and dimensions for the beam needed to be measured in order for the results outlined in the theory section to be calculated. The digital scale was used to give a value for the unknown weight while the vernier calipers were used to measure the width, b, and thickness, t, of the beam, as well as the distance between the load and the strain gauge, L.
The mass, W, added and the voltmeter measurement, V, were recorded for each circuit and collected in four tables which can be found in Appendix A. The mass values were converted from g to N and graphs of the strain gauge voltage against applied load were drawn for the four circuits. The measured voltage for the unknown mass is also included alongside the appropriate tables.
5.1 Potential Divider

The unknown mass gave a reading of 1.130V.

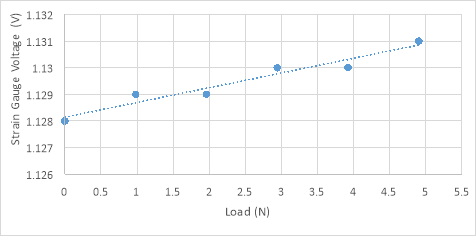
 5.2 Wheatstone Bridge
5.2 Wheatstone Bridge
The unknown mass gave a reading of 0.4mV for the quarter bridge and 0.8mV for the half bridge.
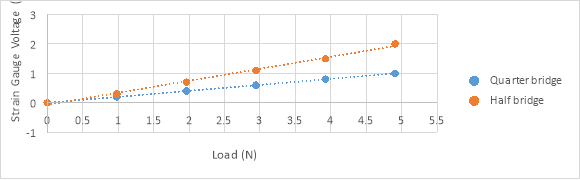
5.3 Wheatstone Bridge with Differential Amplifier

The amplifier circuit increased the values recorded in figure 7 by a factor of 50. The unknown mass gave a reading of 24.2mV.
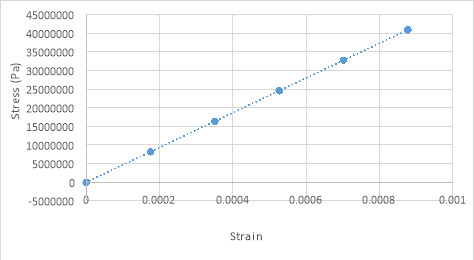
5.4 Stress against strain for the beam
Using the measured values from above and inputting them into equation 4 and equation 5 respectively, a graph of stress against strain can then be plotted. Referring to equation 3, the gradient of this graph then corresponds to Young’s Modulus, which is calculated to be 46.6 GPa.
5.5 Calibration Values
Weight resolution is defined as the smallest increment of weight which the numeric display, in this case the voltmeter, can indicate. (4) Each circuit used during this investigation had a different weight resolution, which was calculated by measuring the initial voltage change from no load to 100g load and comparing this to the resolution of the measuring equipment: for the potential divider, this was ±1mV, and for the other circuits this was ±0.1mV. For example, when the voltage in the potential divider circuit increased by 1mV, the weight increased by either 100g or 200g – the potential divider does not have an absolute weight resolution as multiple load values produced the same voltage reading and therefore the weight resolution is given through a range rather than a definite value.
The weight resolutions increased as expected, with the potential divider providing the least accurate measurements and the quarter bridge with differential amplifier providing the most accurate measurements.
 These weight measurements can be used to estimate the weight of unknown mass by multiplying the recorded voltage for the unknown mass by the weight resolution calculated. This is shown in Table 1 below:
These weight measurements can be used to estimate the weight of unknown mass by multiplying the recorded voltage for the unknown mass by the weight resolution calculated. This is shown in Table 1 below:
|
Electrical Circuit |
Weight Resolution |
Estimate for unknown mass value |
|
Potential Divider |
100g-200g |
113g-226g |
|
Quarter Bridge |
50.0g |
200g |
|
Half Bridge |
25.7g |
205.6g |
|
Quarter Bridge with amplifier |
0.994g |
241.9 g |
The unknown mass was measured to be 236.4g using the digital scales.
As can be seen from figure 1 and figure 2 from the theory section, both the potential divider and Wheatstone bridge circuits are fitted with additional resistors, 1.5kΩ and 680Ω respectively. Known as current limiting resistors, these are necessary to stop the current rising above a certain value – in these circuits it is necessary to limit the current to less than 10mA, calculated by dividing the source voltage of 15V by the circuit resistance of 1.5kΩ (resistor) + 240Ω (strain gauges) in the potential divider circuit, giving a current of 8.6mA. This reduces any measurement errors which could arise from an increase of the strain gauge’s temperature through the Joule effect, where the energy of an electric current is converted into heat as it passes through a resistive material. (5)
As the circuits change from potential divider through to quarter bridge with differential amplifier, the accuracy of the measured voltages increases. This can be demonstrated through the graphs in figures 7, 8 and 9 where it can be seen that the plotted values lie progressively closer to the line of best fit with the graph for the amplifier circuit, shown in figure 9, demonstrating the least deviation from the line. Although this progression agrees with the theory, the actual values obtained differ slightly from the values expected; this is shown through the estimated values of the unknown mass recorded in Table 1. This difference could be the result of a number of factors: uncertainties in the values for the 100g masses used; the fact we are assuming a point load even though the masses provide a distribution of the weight and interference. The use of an AC current produces a small magnetic field which can cause an electromotive force in any wires that are not shielded properly. This small voltage change could be picked up by the voltmeter and slightly alter the measurements.
The unknown mass was measured to be 236.4g by the digital scale. The most accurate estimate calculated by an electrical circuit was 241.9g by the Wheatstone quarter bridge with differential amplifier. The possible reasons for discrepancies between values can include the limitation of the amplifier gain due to electrical noise and temperature changes in the wire. The latter can be a problem as an increase in temperature corresponds to an increase in resistance which can affect measured values. However, this error is reduced in the half bridge configuration as, with a strain gauge sensor on both the top and bottom of the bar, the effect of temperature change cancels itself out.
Finally, the Young’s Modulus value obtained through this experiment is significantly outside the expected range of 190-210 GPa, at 46.6 GPa. This can mainly be attributed to irregularities in the dimensions of the steel beam used – the section of the beam where the gauges were installed was slightly smaller than the rest of the beam to allow for the necessary preparation. Referring back to equation 4 in the introduction section, the inclusion of a 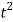 term shows that the thickness of the beam has the greatest effect on the calculated stress, and therefore this discrepancy in values has a significant effect on the value of Young’s Modulus calculated. To achieve a value for Young’s Modulus of 200 GPa, a thickness of 0.47cm would be required.
term shows that the thickness of the beam has the greatest effect on the calculated stress, and therefore this discrepancy in values has a significant effect on the value of Young’s Modulus calculated. To achieve a value for Young’s Modulus of 200 GPa, a thickness of 0.47cm would be required.
To conclude, the experiment outlined in this report was useful in demonstrating the varying levels of accuracy of measurements which can be achieved through different forms of electrical circuits, validating the expectation that weight resolution, and therefore accuracy, would increase as the circuits progressed from a potential divider to a Wheatstone quarter bridge with differential amplifier, with the latter providing the most reliable output voltage results and the highest weight resolution.
However, the result obtained for the Young’s Modulus of steel, of 46.6 GPa, through the measurements recorded in this experiment, highlights how many of the variables associated with electrical circuits have large uncertainties which can lead to extreme unreliability in the data measured and consequently the final results.
The findings of this experiment are statistically insignificant due to the nature of the apparatus used compared to that used in industry. However, it does effectively illustrate the importance of reducing the effect of possible sources of error before an experiment is performed, as well as taking the time to precisely measure all of the necessary results throughout, as a slight inaccuracy in one measurement can significantly affect the final values.
|
Mass (g) |
Weight (N) |
Voltage across Strain Gauge (V) |
|
0 |
0 |
1.128 |
|
100 |
0.981 |
1.129 |
|
200 |
1.962 |
1.129 |
|
300 |
2.943 |
1.130 |
|
400 |
3.924 |
1.130 |
|
500 |
4.905 |
1.131 |
|
Unknown |
– |
1.130 |
Potential Divider
Wheatstone Quarter Bridge
|
Mass (g) |
Weight (N) |
Output Voltage (mV) |
|
100 |
0.981 |
0.2 |
|
200 |
1.962 |
0.4 |
|
300 |
2.943 |
0.6 |
|
400 |
3.924 |
0.8 |
|
500 |
4.905 |
1 |
|
Unknown |
– |
0.4 |
Wheatstone Half Bridge
|
Mass (g) |
Weight (N) |
Output Voltage (mV) |
|
100 |
0.981 |
0.3 |
|
200 |
1.962 |
0.7 |
|
300 |
2.943 |
1.1 |
|
400 |
3.924 |
1.5 |
|
500 |
4.905 |
2.0 |
|
Unknown |
– |
0.8 |
Wheatstone Quarter Bridge with Amplifier
|
Mass (g) |
Weight (N) |
Amplified Voltage (mV) |
|
100 |
0.981 |
9.8 |
|
200 |
1.962 |
19.9 |
|
300 |
2.943 |
30.1 |
|
400 |
3.924 |
40.2 |
|
500 |
4.905 |
50.3 |
|
Unknown |
– |
24.2 |
|
[1] |
H. Eren and C. C. Fung, “Electrical Engineering Vol.II – Instrumentation Systems,” Perth. |
|
[2] |
Omega, “What is a strain gauge?,” [Online]. Available: http://www.omega.co.uk/prodinfo/straingauges.html. [Accessed 17 April 2016]. |
|
[3] |
Electronics Tutorials Staff, “Wheatstone Bridge,” [Online]. Available: http://www.electronics-tutorials.ws/blog/wheatstone-bridge.html. [Accessed 17 April 2016]. |
|
[4] |
Precision Weighing Balances, “Scale and Balance Definitions in Simple Terms,” [Online]. Available: http://www.scalenet.com/applications/glossary.html. [Accessed 17 April 2016]. |
|
[5] |
Comsol, “The Joule Heating Effect,” [Online]. Available: https://www.comsol.com/multiphysics/the-joule-heating-effect. [Accessed 17 April 2016]. |
|
[6] |
D. R. Ngwompo, Measurements Using Strain Gauge Lab Sheet, Bath, 2016. |
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


