RGB Components Color Images Encryption in FRT Ranges

RGB Components Color Images Encryption in FRT Ranges

Somayeh Komeylian

Department of Tel-Communication Engineering, Islamic Azad University South Tehran Branch, Tehran, Iran

Armin Mehrabian

Department of Medical, Mashhad Medical Science University, Mashhad, Iran

Saeed Komeylian

Factory of graduated students, Department of Tel-Communication Engineering, Sharif University of Technology, Tehran, Iran

Latest works are doing on date encryption/color Image in optic range as well as Digital ranges. In this research, color Images encryption has been done by RGB components in FRT ranges for any kind of encryption random phase codes. Moreover, one single-part encryption method has been performed for color twin images. Encrypted twin RGB images by their color map converted to indexed format. One Algorithm used for incorporating two images in order to encrypt in FRT domain. Outlined Algorithm of 15entering parameter involved generally that random phases could be considered as keys for encryption. Unsuitable selection of any keys during encryption will have negative results. Presence of many keys help in building system that’s intensely safe against unpermitted accessibility it could be seen that encrypted images were completely safe against unpermitted time accessibility that has false fractional commands in all three channels.

Keywords: RGB Components; Color Images; Encryption.

By developing Multimedia network, connection and publication techniques, tendency to send and gain Digital Date, especially images, extended a lot. Protecting individual and hiding things for permitted users and ensuring accessibility for legal Data and security considered as the most important subject in connections and image storage. One of the certain ways for immunity is encryption different optic methods recommended well for Digital methods and encrypting images. That consisted of good recognition of (DRPE) Double random phase encryption [1-3]. This method statistically uses Double Random phase in entrance and Fourier phase for input image encryption into a stationary white noise. This method generalization conducted toward fractional Fourier domain and then considerable help has been done by authors and researchers [7, 8]. In addition, many remarkable works are doing on date encryption/color Image in optic range as well as Digital ranges. In the other related works for color Images encryption, RGB color Image RGB components in FRT ranges used for any kind of encryption random phase codes and FRT fractional commands as keys [6]. Moreover, one single-part encryption method has been performed for color twin images [5]. Encrypted twin RGB images by their color map converted to indexed format. One Algorithm used for incorporating two images in order to encrypt in FRT domain. Mentioned Method is Single-part and permitted processing in a simple direction [4].

A. Definition of FRT

Conventionally, The n^th order FRT f_n(x_n) Of a function f(x) is calculated using integral transform kernel given by follow equation [4].

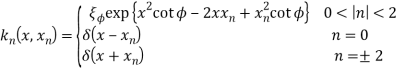(1)

Where

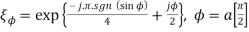(2)

Moreover, X and x_n represent the coordinate systems for the input (zero order) domain and the output (n^th order) fractional domain respectively. The FRT is linear and has the property that it is index additive:

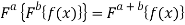(3)

Where a and b are different fractional orders of the FRT.

It is possible to extend the definition of the FRT order beyond ±2

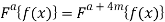(4)

Where m is an integer.

B. Concept of Colored Indexed Images

Colored image in our context is represented as f_n(x. y), where  x and y are spatial coordinates and n denotes the index of primary color components (n=0, 1, 2) f₀(x. y), f₁(x. y) and f₂(x. y) correspond to RGB color components respectively. A colored image con be viewed as a stack as a stack of RGB components forming a m-n-3 array, with each pixel as a triplet corresponding to the values of the primary color components. On the other hand, an indexed image consists of a data matrix and a color map matrix. The color map matrix is an m-3 array of class double containing floating – point values in the range [0, 1], where ‘m’ is a function of the color system and it defines the number of colors it defines. Each row of the color map matrix specifies the red, green, and blue components of a single color. An indexed image uses direct mapping of the pixel intensity values to color map values. The color of each image pixel is determined by using the corresponding value of the data matrix as a pointer into color map. Unlike a colored image (Which is a 3-D matrix), an indexed image is a 2-D array, and simplifies the encryption as the color map is uniquely defined for a given color system. The same can be extracted from the color image and only a 2-D indexed image can be encrypted. Thus the process of encryption and decryption can be carried out in a single channel similar to the gray scale images, and the colored image can be retrieved after adding the color map to the decrypted indexed image [4].

A. Recommended Encryption Algorithm

Colored image in our context is represented as follow equation:

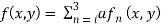(5)

Where, x and y are spatial coordinates and n denotes the index of primary color components (n=0, 1, 2) f₀(x. y), f₁(x. y) and f₂(x. y) correspond to red, green, and blue color components respectively. Each of these components is segregated and the input RGB image p(x, y), to be encrypted, is converted into its indexed format p_i (x, y), by extracting the color map and with each of these components are added. Each of these components encrypted independently using fractional Fourier encryption. The schematic of the proposed encryption technique is shown in Figure (1). The colored image to be encrypted is decomposed in red, green, and blue components and each of these components are combined with indexed image p_i (x, y), and each component is multiplied with random phase functions Φ_r1(x, y), Φ_g1(x, y), and Φ_b1(x, y). The random functions used above are statistically independent of each other. The FRT with different fractional orders along each spatial coordinate is performed for all the color components i. e (a_rx, a_ry) for red, (a_gx, a_gy) for green, and (a_bx, a_by) for blue respectively. The transformed primary color images are then multiplied with three random phase functions Φ_r2(u, υ), Φ_g2(u, υ) and Φ_b2(u, υ) in the fractional domain, where u and υ denote the coordinates in the respective fractional domain. Another FRT is performed subsequently on these images independently with different fractional orders along each spatial coordinates i.e. (b_rx, b_ry) for red (b_gx, b_gy) for green and (b_bx, b_by) for blue, in order to obtain the encrypted images for each of the three color components. In the final step, these three encrypted image are combined to get the colored encrypted image e(x, y).

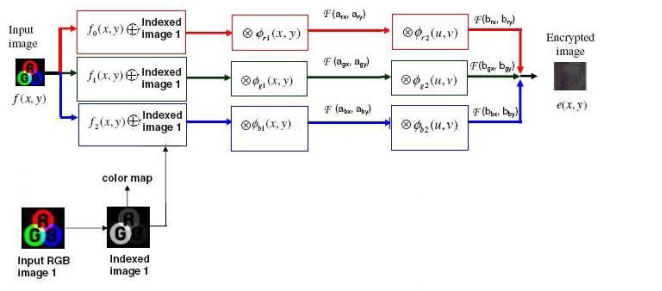
Figure 1: The color image encryption algorithm

B. Recommended Decryption Algorithm

The decryption process is described in Figure (2). The encrypted image is first decomposed into three primary color components. FRT of fractional orders (-b_rx, -b_ry), (-b_gx, -b_gy) and (-b_bx, -b_by) are calculated for the red, green, and blue color components, respectively and are subsequently multiplied with random phase functions Φ^*_r2(u, v), Φ^*_g2(u, v), and Φ^*_b2(u, v) in the fractional domain, where “*” denotes complex conjugate. In the next step, the FRTs of the fractional orders (-a_rx,-a_ry) for red, (-a_gx,-a_gy) for green- and (-a_bx,-a_by) for blue-color images are calculated. Furthermore, indexed image p_i (x, y) is segregated and finally these three components color images are combined to get the decrypted image.

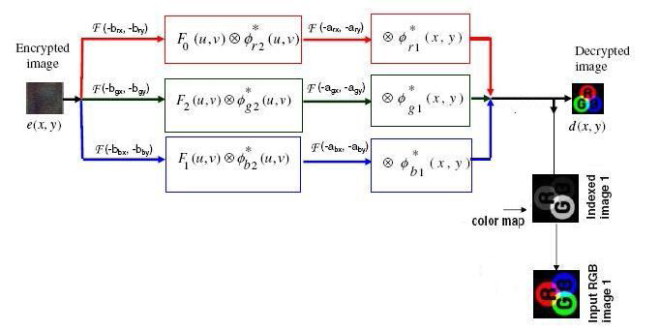
Figure 2: The color image decryption algorithm

Figure (3a) is the main Image of globe and our main Image that will be encrypted. Figure (3b) is lena picture that would be index image incorporated with the main image. P(x,y) that has been shown in Figure (3b), and index image has been shown in Figure (3c) and finally encrypted image resulted as Figure (3d). Now, in encryption process, we must arrange it like this and see that encrypted image of globe will be as follows after separation.

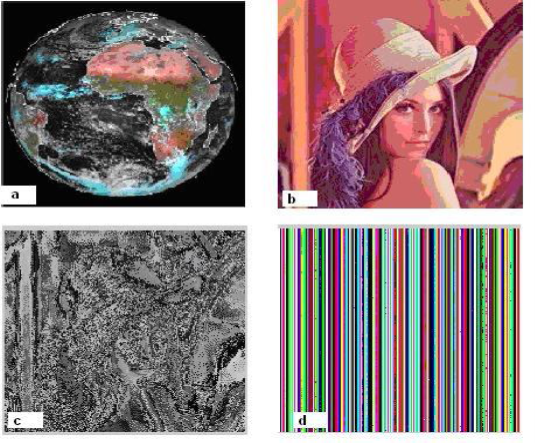
Figure 3: The Result of encryption

In the previous part, observed results of encryption and decryption. Outlined Algorithm of 15entering parameter involved generally that random phases could be considered as keys for encryption. Unsuitable selection of any keys during encryption will have negative results. Presence of many keys help in building system that’s intensely safe against unpermitted accessibility it could be seen that encrypted images were completely safe against unpermitted time accessibility that has false fractional commands in all three channels.

References 

1. P. Refregier, B. Javidi, (1995), Double random Fourier plane encoding, Opt. Lett. 20(1): 767-778.
2. B. M. Hennelly, J. T. Sheridan, (2003), Image encryption and the fractional Fourier transform, Optik, 114(2): 6-15.
3. B. M. Hennelly, J. T. Sheridan, (2003), Double random fractional Fourier plane encoding, Optik, 114(1): 251-262.
4. M. Joshi, K. Singh, (2007), Color image encryption and decryption for twin images in fractional Fourier domain, Optics Communications, 281(1): 5713-20.
5. M. Joshi, K. Singh, (2007), Color image encryption and decryption using fractional Fourier transform, Optics Communications, 279(1):35-42.
6. Z. Liu, S. Li, (2007), Double image encryption based on iterative fractional Fourier transforms, Optics Communications, 275(1): 324-329.
7. Y. Wang, S. Zhou, (2011), A Novel Image Encryption Algorithm Based on Fractional Fourier Transform, IEEE, 978(1): 4244.
8. X. Feng, X. Tian, Sh. Xia, (2011), A Novel Image Encryption Algorithm Based On Fractional Fourier Transform and Magic Cube Rotation, IEEE, 978(1): 4244-9306