Investigation of Masonry Arch Bridges Under Earthquake Loading

Abstract

The design of historical structures revolved around statics with either minimal considerations for horizontal loading or none at all. As such, they are ill-equipped to withstand the extreme loads associated with earthquake excitation. This paper will evaluate the effects of in-plane and out-of-plane dynamic loading on various masonry arch bridge models under plane strain modelling. A constitutive model based on damage-plasticity will be adopted to represent the masonry elements based on historical values for strength, as well as plastic and elastic strain measures. The effects of the backfill, slenderness of piers, soil domain and number of spans in regards to the stability and strength of the structure will be analysed and discussed.

Introduction

Historical masonry arch brides are still being used throughout the world; many instances of this can be seen throughout western Europe and Turkey. As the majority have not been retrofitted in order to improve their seismic capacity, they are at risk of sustaining high levels of damage or even collapse when subjected to earthquake loading.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

Nonlinear dynamic analyses yield the most comprehensive information regarding the stability and safety under such hazardous conditions, as they allow for the study of ductility, damage, force redistribution, as well as possible collapse mechanisms. It is important to note that the observed results are due to the model undergoing excitation based on the specific accelerations and displacements introduced, and as such may vary greatly were different earthquake input data to be applied.

Furthermore, it is impossible to define material and contact properties in such a way, so as they encompass all historical masonry bridges: these vary based on the period, location and construction sequence. As such, the performed analyses assume realistic properties on average in order to create a mechanical characterisation of the various materials composing the model. The discretisation strategy initially was based on the micro-modelling approach, so as to study the effect of nonlinearity on individual bricks and mortar layers. Due to the complexity of the model and the number of elements required, this led to excessive computing times, and as such macro-modelling was adopted. The implications of this will be discussed in Section 2.

Aims & Objectives

Initial Research & Objectives

Initial research revolved around 2 main components: literature research and computational analysis research. Weekly objectives regarding both were set, so as to achieve an understating of masonry structures under dynamics loading and the computational procedures involved to accurately represent those characteristics in a Finite Element Model. Computational analysis was initially done in Abaqus but due to license limitations the models were transferred in Adaptic. A detailed discussion of the implications is discussed in Section 3, which focuses on the expected and observed behaviour of the models under horizontal excitation.

Initial Literature Research

Following an initial background research on masonry structures and their properties, a further study on modelling of masonry elements using finite element software was carried out. Masonry, being a composite material, is a material of large variability of its constituent materials. There are many factors affecting its performance: the bond strength, the materials used and the quality of the workmanship that produced it. Historical masonry is usually characterised by low strength namely due to low mortar strength. This variability and consequent material properties result in different modelling approaches: equivalent frame, equivalent material and micro-modelling (Giamundo et al., 2014). The first approach is suitable for static analyses and as such cannot be applied for nonlinear dynamic purposes. The second approach, also known as the macro-approach, models masonry as a homogenous material with equivalent mechanical properties, while the third, the most refined, models the bricks and mortar separately. This last approach, being the most accurate one, allows for study of local failure of the bricks and mortar (Capozucca et al., 2017). This refinement, however, increases the computational power needed exponentially, and as such the second approach was adopted as it acts as a compromise between accuracy and computational demands. Furthermore, micro-models require in-depth knowledge of the materials being studied, which more often than not is not the case with historical masonry. As such, macro-modelling adopting mean properties was chosen as the modelling strategy. A graphical explanation of the two relevant modelling methods is provided below in Figure 2.1.

Figure 2.1: Micro-modelling (a) & Macro-modelling (b) (Capozucca et al., 2017)

Hacıefendioğlu et al. (2017) showed that variability in the Elastic modulus, Poisson’s Ratio and mass density have a considerable effect on the response of historical masonry arch bridges. However, their analysis showed that variability in the Elastic modulus tends to increase experienced displacements and stresses, while variability in the other material properties generally leads to lower values. Consequently, they observed a maximum change of bridge displacement of approximately 5%, but a number of nodes had a much smaller variability – close to 0%. Based on this a decision was made to use uniform material properties throughout, as the complexity of the constructed models equates to high computational times and including statistical variability would result in much higher computing times with little overall difference for the observed behaviour.

Sevim et al. (2011) studied the effects of finite element model calibration extensively to show that experimental natural frequencies, mode shapes and damping can differ substantially from finite element outputs. Therefore, they recommend that computational models be calibrated, so as to match values obtained from enhanced frequency domain decomposition and stochastic subspace identifications for the true mode shapes and damping ratios. As the models discussed in this paper are manually generated this is not possible; therefore, Rayleigh damping coefficients will be assumed as 5%.

Özmen and Sayın (2018) created a 3D model of the Dutpınar masonry bridge in Maden under linear conditions, which can be seen below in Figure 2.2.

Figure 2.2: Dutpınar Bridge Model (Özmen and Sayın, 2018)

Their study focused on the time histories of the maximum and minimum principle stresses and strain; these are later used to identify potential locations where damage may be incurred. The obtained values may not, however, be entirely accurate due to the approach taken. The bridge itself experiences horizontal loading from its sides, while any degrees of freedom associated with the bases are assumed fully fixed. Consequently, the effect of the soil domain on the bridge’s behaviour cannot be observed. Furthermore, both the masonry elements and backfill are modelled as elastic and the interaction between the two cannot be studied. Therefore, it is probable that the obtained values for stresses and strains are inaccurate due to plasticity and hysteresis. This paper will provide evidence of the importance of each of these factors on the nonlinear dynamic response of historical masonry arch bridges.

Karaton et al. (2017) performed a nonlinear seismic response study of the Malabadi Bridge, which was constructed in the 12^th century. This particular bridge is the especially wide and spans 38.6 m. The model is provided below in Figure 2.3.

Figure 2.3: Malabadi Bridge Model (Karaton et al., 2017)

A smeared crack model, which includes tensile cracking and compressive crushing is adopted to model the masonry material, as it allows for damage and plastic deformations to be studied under applied loading. Cracking is initially observed at the upstream face of the bridge, close to the main arch base. No signs of damage are yet present on the downstream face of the bridge. Additional cracking zones then develop at the middle region of the arch face due to movement the arch is forced to undergo. Further excitations lead to crack propagation until numerical convergence can no longer be achieved. A summary of the final damage zones is provided in Figure 2.4. It is unclear whether the initial damage close to the base is due to the bridge’s geometry or nonlinear effects. However, the damage pattern at midspan shows that the arch itself is the most vulnerable part of the bridge. It can thus be concluded that nonlinearity will play a defining role in masonry bridge behaviour. However, as mentioned previously, it is also likely that the amount of backing and backfill on top of the arches, as well as the presence of a soil domain on either side of the bridge will most probably have an impact on the dynamic performance of the models as well, be it to stabilise and mitigate damage, or increase it compared to a fixed model.

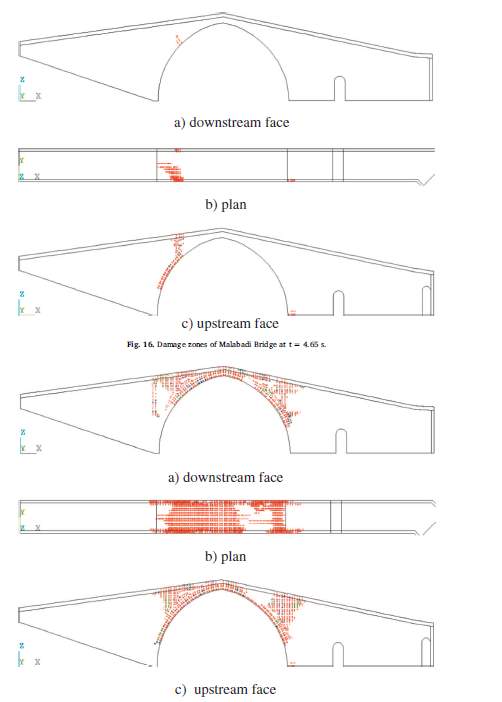
Figure 2.4: Damage Zones of Malabadi Bridge Model (Karaton et al., 2017)

Pelà et al. (2009) studied the S. Marcello Pistoiese Bridge – a multi-span historical arch bridge. Micro modelling was employed in order to complete an inelastic pushover analysis. Their results confirm the studies of Karaton et al. (2017), as can be seen in Figure 2.5.

Figure 2.4: Brick Displacement of S. Marcello Pistoiese Bridge (Pelà et al, 2009)

The arches themselves are the most vulnerable part of the bridge with the greatest displacements being recorded in those regions. Pushover analyses are attractive from a computational point of view but might be subject to bias due to the choice of the control node, which is used to evaluate reference displacements. Thus, a fully nonlinear time-history analysis should be performed so that a better understanding of the dynamic behaviour may be obtained.

Scope

Building on the initial aims and objectives, several critical areas of importance were identified in regards to masonry arch bridge behaviour and modelling techniques. As nonlinear dynamic analyses are computationally expensive a number of simplifications have been adopted: all models were based on plane strain and macro-modelling, as running a comprehensive 3D model based on the micro-modelling was deemed unrealistic. The first model consisted of a 3-span bridge which modelled masonry arches and backing explicitly, as well as backfill and an elastic layer on top. In-plane accelerations were introduced to the base of the structure, as well as at the ends of the span. This model will be used as a basis for comparison as further models are developed. Points of study will include the effect of the backfill and backing on the stability and safety of the structure, as well as the introduction of a soil domain on either side of the bridge. Furthermore, the number of piers and their slenderness is expected to influence the nonlinear behaviours as well, and such models with different number of spans and pier heights will be constructed. Once completed, the same procedure will be applied to the study of out-of-plane dynamic loading.

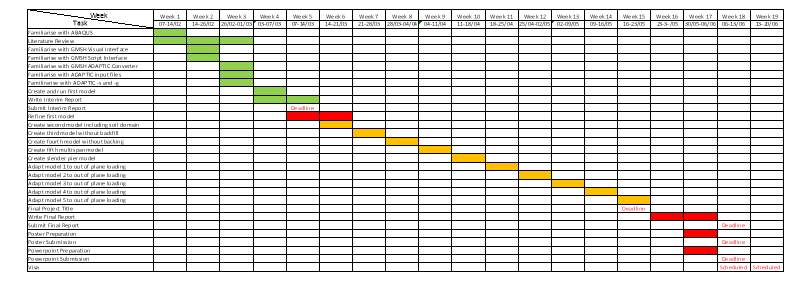
A Gannt Chart outlying the process is shown below in Figure 2.5.

Figure 2.5: Gantt Chart Outlying Objectives

Research Methodology & Approach

The discussed analyses of the bridge models are carried out using two software programmes – Gmsh and Adaptic. In order to facilitate the use of Adaptic, geometric properties and meshes defining the models were first created in Gmsh and later converted into Adaptic input files. Gmsh allows the user to partition the model in different physical groups, which represent the different materials comprising the bridge. This can be seen in Figure 3.1.

Figure 3.1: Physical Groups of Model

The yellow elements represent the masonry arches and backing of the bridge, the blue the backfill while the green represent ballast on top. The bridge itself has a clear span of 12320 mm with 2000 mm by 5000 mm high piers.

Furthermore, surfaces can be identified, where the model is restrained from moving. In the model completed, a strip of a bridge is created with the in-plane direction being defined as parallel to the x-axis. As such, the finite element model is unrestrained and allowed to move freely along this vector, as the earthquake loading is applied in that direction. These surfaces are shown in Figure 3.2.

Figure 3.2: In-plane Surfaces

Since plain strain is assumed and no loads are applied orthogonally, the model is restrained along the y-axis, which represents the out-of-plane direction. This can be seen in Figure 3.3.

Figure 3.3: Out of Plane Restrained Surfaces

As Adaptic has no visual interface in regards to its input files, the weight of each element group was defined in Gmsh as a uniformly distributed load acting across these elements. Figure 3.4 defines a common load across all masonry elements.

Figure 3.4: Self-weight of Masonry Elements

The constitutive model used for the masonry elements is an effective stress-based plasticity model with a damage model based on plastic and elastic strain measures. It describes well the increase in strength and displacement capacity for increasing confinement levels, which makes it an apt choice for modelling homogenously defined masonry.

Conclusion

Historical masonry arch bridges are particularly vulnerable to earthquake loading, but the extent of the hazard cannot be measured accurately without modelling all parts comprising the bridge, as it is possible for parts of the bridge to stabilise the behaviour while for others lead to greater damage and destabilisation than expected. This is a particularly challenging task, due to lack of information regarding the characteristics of historical bridges and their inner workings. Thus, simplifying the modelling procedure by not modelling different regions such as the backfill and soil domain leads to results that are even more unreliable.

Appendix A: References

• Capozucca, R., Magagnini, E. and Pace, G. (2017). FE Modelling of Experimental Brickwork Masonry Building Under Eccentric Shear Force. The Open Civil Engineering Journal, 11(Suppl-5, M3), pp.1036-1058.
• Giamundo, V., Sarhosis, V., Lignola, G., Sheng, Y. and Manfredi, G. (2014). Evaluation of different computational modelling strategies for the analysis of low strength masonry structures. Engineering Structures, 73, pp.160-169.
• Hacıefendioğlu, K., Başağa, H. and Banerjee, S. (2017). Probabilistic analysis of historic masonry bridges to random ground motion by Monte Carlo Simulation using Response Surface Method. Construction and Building Materials, 134, pp.199-209.
• Karaton, M., Aksoy, H., Sayın, E. and Calayır, Y. (2017). Nonlinear seismic performance of a 12th century historical masonry bridge under different earthquake levels. Engineering Failure Analysis, 79, pp.408-421.
• Özmen, A. and Sayın, E. (2018). Seismic assessment of a historical masonry arch bridge. Journal of Structural Engineering & Applied Mechanics, 1(2), pp.95-104.
• Pelà, L., Aprile, A. and Benedetti, A. (2009). Seismic assessment of masonry arch bridges. Engineering Structures, 31(8), pp.1777-1788.
• Sevim, B., Bayraktar, A., Altunişik, A., Atamtürktür, S. and Birinci, F. (2011). Finite element model calibration effects on the earthquake response of masonry arch bridges. Finite Elements in Analysis and Design, 47(7), pp.621-634.