Microgrid Energy Management Using a Two Stage Rolling Horizon Technique
| ✅ Paper Type: Free Essay | ✅ Subject: Engineering |
| ✅ Wordcount: 4924 words | ✅ Published: 23 Sep 2019 |
Microgrid Energy Management Using a Two Stage Rolling Horizon Technique for Controlling an Energy Storage System.
Abstract—In this paper, a new Energy Management (EM) strategy is proposed which uses a two-stage rolling horizon (RH) technique to control a battery energy storage system (BESS). The objectives of the control are to increase the self-consumption of the renewable energy resources (RES) and minimize the daily cost of the energy drawn from the main electrical grid. Mixed integer linear programming (MILP) optimization is used as a part of the RH technique to obtain the optimal control settings for the BESS. Using the RH technique and processing the control signals with two different time periods gives more optimal BESS settings which can overcome the errors associated with load prediction and operational constraints. Simulation results demonstrate that the proposed strategy can benefit MG customers and satisfy different market conditions.
Keywords—Energy management system, Microgrid, Mixed integer linear programming, Rolling Horizon, Optimization.
I. Introduction
The growth of renewable energy sources (RES) in the electricity grid together with the increasing use of electricity for transport and heating, ventilation and air-conditioning requires a new vision for future transmission and distribution grids. The Global Smart Grid Federation report claims that the existing power grid networks are not equipped enough to meet the demands of the 21st century [1].
Increasing the complexity and variability of generation sources introduces a new type of electric grid which needs more innovation to solve its challenges, manage operation, and control its expansion.
The concept of the Micro-grid (MG) is a promising and welcome idea that introduces engineered solutions to challenges that face the electricity grid, in an efficient, reliable, and economic way and Micro-grid Energy Management (MGEM) is the most important topic regarding MGs particularly as it has to address both technical and commercial challenges [2].
There is much research focusing on MGEM. In [3], the design and experimental validation of an adaptable MGEM is implemented in an online scheme. In this case, the author aims to minimize the operating costs and the disconnection of loads by proposing an architecture that allows the interaction of forecasting, measurement and optimization modules, in which a generic generation-side mathematical problem was modelled
In [4], Mohsen et al. introduce two dispatch-optimizers for a centralized MGEM system as a universal tool. Scheduling the unit commitment and the economic dispatch of the MG units is achieved using an improved real-coded GA and an enhanced Mixed Integer Linear Programming (MILP) based method. The authors in [5] implement an economic dispatch strategy with MILP to determine the optimal operation for a hybrid energy system using steady-state models. The hybrid system is composed of biomass, biogas, photovoltaic panels, a diesel generator and a battery bank.
Daniel & Erlon [6] present a mathematical model for the EM problem of an MG by means of a MILP approach. The objective is to minimize the operating costs subject to economical and technical constraints over a planning horizon through determining a generation and a controllable load demand policy. The results show the efficiency of the proposed approach to deal with extreme situations with the misbehaving of the forecasted consumption or even with unstable generation.
A novel MGEM system based on a rolling horizon (RH) strategy for a renewable-based MG is proposed in [7]. The proposed technique is implemented for an MG, which consists of two wind turbines, photovoltaic panels, a diesel generator, and an energy storage system in which a mixed integer optimization problem based on forecasting is solved for each decision step. Based on a demand-side management technique, the MGEM provides online set points for each generation unit and signals for consumers. The results show the economic revenue of the proposed strategy
The authors in [8] focus on the development of optimization-based scheduling strategies for the coordination of MGs. Simultaneous management of energy demand and energy production are used within a reactive scheduling approach to solve the problem of uncertainty associated with generation and consumption.
Martin et al. [9] presented an EMS prototype for an isolated renewable-based MG which consists of two stages: a deterministic management model is formulated in the first stage followed by integration into a RH control strategy. The advantage of this proposal considers the management of energy sources in addition to including the possibility of flexible timing of energy consumption (demand management) by modelling controllable and uncontrollable loads.
The research presented in this paper focuses on using an energy management based on a two-stage rolling horizon strategy. The objectives are to increase the self-consumption of the renewable energy resources and to minimize the daily cost of the energy drawn by the MG from the main electrical grid, and thus achieve good economic performance for the MG customers and minimize the dependency of the MG on the main electrical grid. The effect of using different tariff schemes to suit different market conditions is also demonstrated as it has a direct effect on the optimal settings of the energy storage system control and on the overall economic results.
II. Microgrid description
The proposed MG used in this paper consists of eight houses located in a UK based community, a Photovoltaic (PV) generation system and a Battery Energy Storage System (BESS). The MG is also connected to the main electric grid. The electrical load profile of the UK community is created using a model from the Centre for Renewable Energy Systems Technology (CREST) created by Richardson and Thompson [10]. The PV generation profiles used in this paper are obtained from data available at the PVOutput website [11] for the ETB 22kW station located at the University of Nottingham. The BESS used for this analysis has a rated capacity of 80kWh and a rated power of 15kW. The operation of the microgrid was simulated under various operating conditions using the Matlab/Simulink simulation environment.
III. proposed energy management strategy and the main implementation steps
The MGEM strategy proposed in this paper focuses mainly on increasing the self-consumption of the RES within an MG, minimizing the daily cost of the energy drawn from the main electrical grid (called the “Community Power Flow” (CPF) in this work) by the MG and also the dependency of the MG on the main electric grid. The controller generates a charge/discharge reference for the BESS, which directly controls the community power flow. This strategy uses a MILP optimization process as a part of the RH technique to obtain the optimal control settings for the BESS (located in the MG) to minimize the daily cost of energy and maximize self-consumption. For the first stage, an optimization process is performed for one day ahead to determine the reference values for the CPF to be drawn from the grid that minimizes the daily cost of energy. This optimization process is performed using a predicted profile for the load and the generation, which has a 15-minute sample period for one day ahead. The reference values obtained for the CPF also have a 15-minute sampling time.
The reference values for the CPF are then processed using a second control stage. During this stage, these values are used as well as a predicted data for the load and generation with sampling time of 1 minute and for only 15 minutes ahead, to determine the optimal settings for the BESS (i.e. 1 optimal setting every 1 minute for 15 minutes ahead). The optimal settings obtained for the BESS will be the actual reference values for the community power flow to ensure minimizing the daily cost of the energy drawn from the main grid. This second stage helps to compensate for imperfect predictions from the first stage and the constraints associated with the operating limits of the BESS.
The RH theory depends on repeating a defined process every fixed time interval and obtaining new results [7], [9]. The two stages described above are repeated every fixed time interval (15 minutes) where a new optimization is performed based on an updated forecast of generation and consumption for the next time interval and feedback of each device status at the end of the previous interval: a new, more accurate optimized setting for the BESS is therefore obtained. The updated forecasts for generation and consumption are obtained from a new prediction over the two stages. For the first stage, a prediction for one day ahead (with a sampling time of 15 minutes) starting from the end of the previous 15 minutes is made, and for the second stage a prediction for only 15 minutes ahead (with a sampling time of 1 minute) starting from the end of the previous 15 minutes is made. Using the RH technique helps in mitigating errors associated with the load prediction and the uncertainty associated with the control signal – e.g. tracking and updating the status of the units in the MG by repeating the optimization process several times. In addition, using the RH strategy, it is possible to move from performing optimization over one day only (without considering the past or the following day, which could affect the results) to a new process of working over a longer continuous period (several days, weeks or even months). The RH strategy enables the MGEM to take into account what happens the following day and the optimization process now covers more than one day. Through this process, earlier actions regarding charging and discharging of the BESS can be accounted for.
The main implementation steps of the proposed strategy are summarized in the flowchart shown in Fig 1.
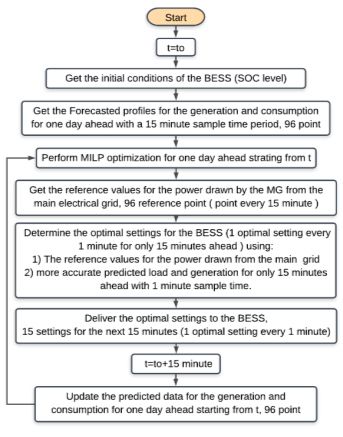
Fig. 1. The main implementation steps of the proposed strategy
To implement this strategy. First, a cost function has to be defined that minimizes the daily cost of the energy drawn from the main grid and all the constraints associated with it. In addition, the BESS should be modeled including any constraints associated with its operation.
A. Objective function formulation
The objective function is formulated to minimize the daily cost of the energy drawn from the main grid “
” and to increase the self-consumption of the RES generated by the MG. This cost can be developed in terms of payments and incomes. The payments include the cost of purchased electricity from the main electrical grid; incomes consider the revenue of the electric energy sold to the main electrical grid – the excess energy produced by the MG PV generation after satisfying the MG consumption and charging the BESS.
The daily cost of the energy drawn from the main grid can be formulated as follows:
(1)
where:
: The daily cost of the energy drawn by the MG from the main electrical grid (£/day)
: The daily cost of the purchased electrical energy from the main electrical grid (£/day)
: The daily income of the exported electrical energy to the main electrical grid (£/day)
These terms can be described as follows:
where:
: Time of day starts at (12 am)
: Time of day end (after 24 hours)
: Sampling time; step size of each optimal solution (1 min.)
: Purchase electricity tariff from the main grid (£/kWh)
: Sale electricity tariff to the main electrical grid (£/kWh)
: Electric power losses across the MG at time interval “t” (kW)
: Electrical load demand at time interval “t” (kW)
: Electric power produced by BESS at time interval “t” (kW)
: Electric power generated by the PV system at time interval “t” (kW)
B. Power balance equation of the MG
The balance equation of the total active power in the MG is formulated as follows:
where:
: The power drawn by the MG from the main electrical grid at time interval “t” (kW), +P means the MG imports power from the main grid, -P means the MG exports power to the main grid.
: The electrical power produced by the BESS at time interval “t” (kW), +P means that the BESS discharges, -P means that the BESS charges.
C. Battery energy storage system modeling and constraints
The constraints associated with the operation of the BESS are formulated as follows:
1) BESS power output
(5)
where
is the maximum power that can be produced by the BESS (kW), +P means the maximum discharge power, -P means the maximum charge power.
2) BESS State of charge (SOC)
(7)
(8)
where:
: Stored energy in the BESS at time interval “t” (kWh)
: Stored energy in the BESS at time interval “t-1” (kWh)
: Discharge power from the BESS at time interval “t” (Kw)
: Charge power in the BESS at time interval “t” (kW)
: Efficiency of discharging and charging respectively.
: Battery capacity (kWh)
,
: Maximum and minimum state of charge limits of the BESS respectively
3) SOC variation
This constraint corresponds to the transition between two states during two consecutive settings, which reflects max ramp up/down rate for the BESS power.
(9)
where
is the variation of the state of charge during charging/discharging periods and
is the maximum acceptable variation of the state of charge for both charging and discharging periods.
4) Power converter losses and efficiency
The power losses in the power converter which is used for the control of the BESS and for grid interface, should be taken into consideration.
where:
: Converter output power at time interval “t” (kW)
: Discharge power from battery at time interval “t” (kW)
: Charge power in the battery at time interval “t” (kW)
: Converter efficiency.
: Constant losses in converter (kW)
D. The power drawn from the main electrical grid
The power drawn by the MG from the main electrical grid has also a number of constraints as follows:
(11)
where
,
are the maximum and the minimum power that can be drawn from the main electrical grid respectively (kW). This constraint is used to minimize the imported power from the main grid and increase self-consumption of RES.
IV. Mixed Integer Linear Programming optimization
MILP is a mathematical optimization program used to solve constrained optimization problems of applications where the constrained optimization problem contains a set of variables, an objective function and a set of constraints [12], [13]. The role of the optimization is to find the best solution for the objective function in the set of solutions that satisfy the constraints (constraints can be equations, inequalities or linear restrictions on the type of a variable).
The mathematical formulation of the MILP problem is expressed as follows:
Objective:
Constraints:
C, b are vectors and A is a matrix,
A solution that satisfies all constraints is called a feasible solution. Feasible solutions that achieve the best objective function value are called optimal solutions.
There are three different approaches to solving MILP, namely, Branch and Bound, Cutting Plane and Feasibility Pump. MILP problems are generally solved using a branch-and-bound algorithm. Basic LP-based branch-and-bound algorithms (Known as Tree search) can be discussed as follows. Start with the original mixed integer linear problem and remove all restrictions, the resulting problem is called ‘‘linear programming relaxation’’ of the original problem, which is solved using the tree search algorithm. The tree is built using three main steps. Branch: pick a variable and divide the problem in two sub problems at this variable. Bound: solves the LP-relaxation to determine the best possible objective value for the node. Prune: prune the branch of the tree (i.e. the tree will not develop any further in this node) if the sub problem is infeasible [14].
For example, to optimize the objective function formulated in 1. First, the problem is solved without any constraints and a list of initial variables and solutions are obtained. Second, the constraints are applied over the obtained solutions and the infeasible ones are refused. Third, the variables which give a feasible solution are then used to generate more variables and the problem is solved again with those variables until the optimal solution is obtained.
V. Simulation results and discussion
The following results are obtained from simulation for the MG defined in section II using the parameters shown in table 1.
Different tariff schemes are used in this research to represent the various market conditions and to show the capability of the proposed strategy to get the best operation scenario with different tariff schemes. For purchasing electricity from the main grid, a time of use tariff (TOU) and a real time pricing tariff are used [15]. For selling electricity to the main grid, a fixed type tariff is used [16], [17]. The tariff schemes which are used in this research tariffs are shown in Fig. 2.
Table 1. Microgrid parameters used in the simulation
|
Parameter |
Value |
Parameter |
Value |
|
|
15 min. |
|
0.33 kW |
|
Battery capacity |
80 kWh |
|
0.95 |
|
|
20 % |
|
-12 kW |
|
|
90 % |
|
12 kW |
|
|
-12 kW |
|
12 kW |
|
|
12 kW |
|
12 kW |
|
,
|
0.9 |
|
15 min. |
|
|
2% of
|
||
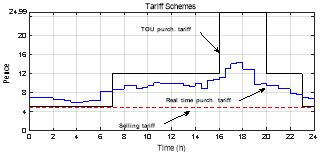
Fig. 2. Purchasing and selling tariff schemes
A. EM results using MILP optimization
In this section, the first stage of the proposed strategy is demonstrated where an optimization process is performed using predicted profiles for the load and generation with a sample period of 15 minutes for one day ahead. The reference values obtained for the CPF have a 15-minute sample time for one day ahead. MILP optimization results of the first stage are shown in Fig 3.
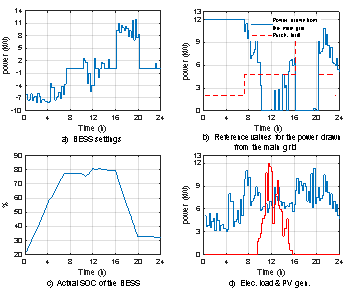
Fig. 3. Optimal settings for the BESS, reference values for the power drawn from the main electrical grid and the SOC of the BESS using MILP optimization with a sample time of 15 minutes
From Fig 3, it is observed that the optimization strategy succeeded in 1) minimizing the electric energy purchased from the main grid at the peak hours (from 4 pm to 8 pm, when the purchase electricity tariff from the main electrical grid is high as shown in Fig 3b). 2) maximizing the self-consumption of the generated PV energy to feed the load within the MG – no export is seen in Fig 3b. 3) maximizing the charging of the BESS at off peak times (from 11 pm to 7 am, where the purchasing electricity tariff from the main electrical grid is low) and using this to feed the load during the rest of the day – as seen in Fig 3c. The optimization strategy takes into consideration the BESS modelling and constraints, and manages to keep the SOC of the BESS and all other constraints associated with it within limits (SOC between 20 and 90 %, maximum charging/discharging power is 15kW) as shown in Fig 3a and 3c.
B. EM results using the proposed two stage RH strategy with TOU purchasing tariff scheme
In this section, the proposed two stage RH strategy is used to derive the optimal control signals for the MG. The load and PV generation profiles used in this part have a 1-minute sample time and are demonstrated for two different consecutive days.
The results obtained in Fig 4 show that the proposed strategy succeeded in determining the optimal settings for the BESS that minimize the daily cost of the energy drawn from the main grid. The optimal settings for the BESS have a 1-minute sample time. It can be seen from Fig 4a and 4d that more accurate predicted load and generation profile, with a 1-minute sample time, are used in this stage to deliver the 1-minute sample time optimal settings for the BESS. These settings compensate for any change in the load and keeps the actual CPF close to the reference through the day as shown in Fig 4b.
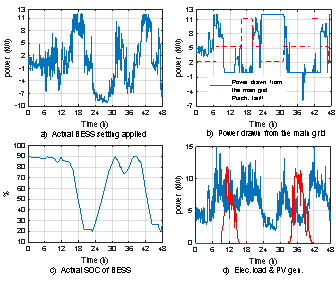
Fig. 4. Obtained results using RH over 2 different consecutive days
Using TOU tariff scheme, the BESS charges at off peak time when the purchase tariff is low and uses it to feed the load at mid-peak and peak times. The results show that the RES are used to feed the load within the MG and the extra energy is saved in the BESS to be used later as shown in Fig 4a between hours 10-12 and between 34 -37. The extra energy that cannot be saved in the BESS due to the SOC limits, are exported to the main electrical grid as shown in Fig 4b between hours 37-38. The daily cost of the energy drawn from the main grid is reduced from £34 to £18.4 for the 2 days by using the BESS and the proposed strategy (i.e. reduction percentage is 45.9% per day).
C. EM results using the proposed two stage RH strategy with real time purchasing tariff scheme
In this section, the system is simulated using real time purchasing tariff instead of TOU tariff. The results obtained in Fig 5a show that changing the tariff scheme, affects the energy drawn by the MG from the main electrical grid. The operation scenario of the BESS and the SOC curve are affected also by changing the tariff scheme as seen in Fig 5a and 5c. The new operation scenario of the BESS shown in Fig 5a is delivered to minimize the daily cost of the energy drawn from the main grid in this case.
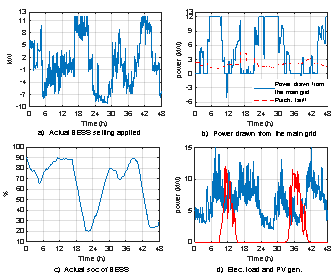
Fig. 5. Obtained results using RH over 2 different consecutive days with a real time pricing scheme
The obtained results confirm the capability of the proposed strategy to deal with different tariff schemes and to achieve good results and to ensure system performance in an economic way.
D. EM results with and without using the second stage of the proposed RH strategy.
Fig 6 shows the actual power drawn from the main electric grid with and without using the second stage of the proposed RH strategy that compensates for the load changes and delivers more optimal settings to the BESS. As seen in Fig 6, without the second processing stage, the generated power from the RES is exported to the main electrical grid at a non-proper time period (such as between hours 33 and 37) which reduces the self-consumption of the RES within the MG; Also, the MG imports energy from the main grid at the peak time periods (between hours 40 and 44) which increase the daily cost of the energy drawn from the main grid.
The second processing stage succeeded in making the actual power drawn from the main grid follow the reference values obtained from the optimization as shown in Fig 6, and also reduced the daily cost of the energy drawn from the main grid from £9.44/day (i.e. in case of using the first optimization stage only) to £9.19 /day.
On the other hand, the constraints and limits associated with the operation of the BESS (such as SOC limit or the maximum value of charge/discharge power) do not allow the optimal settings of the BESS to be executed at certain times, and in this case, the real power drawn from the main grid deviates from the reference values obtained from optimization as shown in Fig 6 (zoom). This happens after using all the solutions available to overcome this problem.
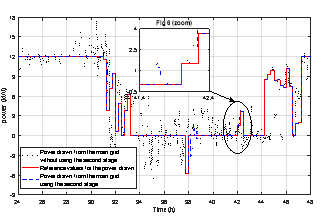
Fig. 6. The actual power drawn from the main grid with and without using the second stage of RH process
VI. Conclusion.
The new approach to MGEM introduced in this research increases the self-consumption of the renewable energy resources (RES) within the MG, minimizes the daily cost of the energy drawn from the main grid and reduces the dependency of the MG on the main grid.
Using MILP optimization, the BESS is used to ensure the MG community power flow follows the reference with minimum errors.
Using a second processing stage more accurate settings for the BESS can be derived at a faster sampling time and therefore a more accurate response to load changes can be achieved to keep the actual community power flow close to the reference values obtained from the first optimization process.
Repeating the first and the second processing stages every fixed time interval using a RH technique, enables errors associated with load prediction to be reduced. The proposed strategy also managed to maintain BESS behaviour within the constraints associated with the operation of the MG (power constraints and BESS constraints).
Simulating the system using different tariff schemes demonstrates the efficiency of the proposed strategy to deliver appropriate economic solutions under various market conditions
Acknowledgment
This work is supported by the Egyptian Government- ministry of higher education (cultural affairs and missions sector) and the British Council through Newton-Mosharafa fund.
References
[1] G. S. G. Federation, “Global smart grid federation report,” Global Smart Grid Federation, pp. 15, 2012.
[2] A. Kowalczyk, A. Włodarczyk, and J. Tarnawski, “Microgrid energy management system.” pp. 157-162, 2016.
[3] A. C. Luna, L. Meng, N. L. Diaz, M. Graells, J. C. Vasquez, and J. M. Guerrero, “Online energy management systems for microgrids: experimental validation and assessment framework,” IEEE Transactions on Power Electronics, vol. 33, no. 3, pp. 2201-2215, 2018.
[4] M. Nemati, M. Braun, and S. Tenbohlen, “Optimization of unit commitment and economic dispatch in microgrids based on genetic algorithm and mixed integer linear programming,” Applied Energy, vol. 210, pp. 944-963, 2018.
[5] A. Gupta, R. Saini, and M. Sharma, “Steady-state modelling of hybrid energy system.” pp. 1-10, 2009.
[6] D. Tenfen, and E. C. Finardi, “A mixed integer linear programming model for the energy management problem of microgrids,” Electric Power Systems Research, vol. 122, pp. 19-28, 2015.
[7] R. Palma-Behnke, C. Benavides, F. Lanas, B. Severino, L. Reyes, J. Llanos, and D. Sáez, “A microgrid energy management system based on the rolling horizon strategy,” IEEE Transactions on Smart Grid, vol. 4, no. 2, pp. 996-1006, 2013.
[8] J. Silvente, G. M. Kopanos, E. N. Pistikopoulos, and A. Espuña, “A rolling horizon optimization framework for the simultaneous energy supply and demand planning in microgrids,” Applied Energy, vol. 155, pp. 485-501, 2015.
[9] M. P. Marietta, M. Graells, and J. M. Guerrero, “A rolling horizon rescheduling strategy for flexible energy in a microgrid.” pp. 1297-1303, 2014.
[10] I. Richardson, and M. Thomson, “Domestic electricity demand model-simulation example,” Data Sets and Software (CREST), 2010.
[11] ETB_UoN_Notts_UK, “Daily ETB_UoN_Notts_UK 22kW,” Available at : https://pvoutput.org, 2016.
[12] M. Jünger, T. M. Liebling, D. Naddef, G. L. Nemhauser, W. R. Pulleyblank, G. Reinelt, G. Rinaldi, and L. A. Wolsey, ” 50 Years of Integer Programming 1958-2008: From the Early Years to the State-of-the-art”: Springer Science & Business Media, 2009.
[13] J. P. Vielma, “Mixed integer linear programming formulation techniques,” SIAM Review, vol. 57, no. 1, pp. 3-57, 2015.
[14] J. C. Smith, and Z. C. Taskin, “A tutorial guide to mixed-integer programming models and solution techniques,” Optimization in Medicine and Biology, pp. 521-548, 2008.
[15] “purchasing electricity tariffs in UK ” Available at: https://www.greenenergyuk.com.
[16] “Selling electricity tariffs in UK,” Available at: https://www.gov.uk/feed-in-tariffs.
[17] “Feed-in Tariff Generation & Export Payment Rate Table,” Available at : https://www.ofgem.gov.uk/system/files/docs/2018/01/fit_tariff_table-_january_2018.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


