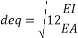Investigation of Subgrade Reaction Coefficient in Sandy Soil
| ✅ Paper Type: Free Essay | ✅ Subject: Engineering |
| ✅ Wordcount: 2914 words | ✅ Published: 31 Aug 2017 |
Numerical investigation of subgrade reaction coefficient in sandy soils
Adel Asakereh1, Hassan Jamali2*, Masoud mossafa1
1 Civil Department, University of Hormozgan, Bandar Abbas, Iran
2Young Researchers and Elite Club, Sabzevar Branch, Islamic Azad University, Sabzevar,
Abstract
The soil-foundation interaction is one of the most important issues in geotechnical engineering relating to soil behavior against side loading. Winkler’s model is the first and simplest method for considering the soil-foundation interaction. Because to determine the coefficient of the subgrade reaction of the soil before designing structure is vitally important, so, experimental, analytical and numerical methods have been proposed. This research chose a ground characteristic that is in Bandar Abbas (Iran). Purpose is to compare the proposed experimental formulae for determining the coefficient of the subgrade reaction with its corresponding values resulting from the behavioral models. Finite element analysis was performed by Plaxis software and important parameters were proposed by the engineers. Results show increasing footing diameter leads to a decrease in the coefficient of the subgrade reaction due to increasing load area which results in increasing settlement. It is found that increasing each of the strength parameters of the soil can be expected to have an effect on increasing the subgrade reaction, although this increase depends on footing diameter. Also in sand soils, the soil cohesion effects on the increase of the subgrade reaction coefficient more than the internal friction angle.
Keywords: Elasticity coefficient, Mat foundation, Subgrade reaction coefficient, Bandar Abbas City, Finite element analysis
- Introduction
The application of mat foundations has a long history. This type of foundation has shown a very good performance in transferring construction forces to the ground. Currently in most cases, engineers use a constant value for the subgrade reaction coefficient to analyze the mat flexible foundations. This constant is obtained from geotechnical experiments such as plate loading. Many researchers have studied soil subsidence and the subgrade reaction coefficient using plate loading test [1-9].
|
Nomenclatures |
|
|
B |
Diameter of footing (m) |
|
|
Minimum marginal dimension of footing(m) |
|
c |
Cohesion (kPa) |
|
d |
Plate thickness (m) |
|
Df |
Embedment depth of foundation(m) |
|
|
Soil elasticity modulus (kPa) |
|
EI |
Flexural rigidity of footing (kN.m2) |
|
EA |
Axial rigidity of footing (kN.m2) |
|
|
Height of ith layer (m) |
|
If , Is, Id |
Dimensionless coefficients |
|
ks |
Subgrade Reaction Coefficient (kN/m3) |
|
m |
Constant coefficients |
|
P |
Vertical pressure (kPa) |
|
Greek Symbols |
|
|
v |
Poisson ratio |
|
|
Vertical Displacement (m) |
|
|
Angle of friction (Degree) |
|
|
Unit weight (kN/m3) |
|
|
Dry unit weight (kN/m3) |
The application of a uniform reaction coefficient over all of the foundation means neglecting the conditions of a continuum for the soil and the effects of cut in the soil layers. One of the fundamental issues in designing and calculating the foundations is the problem of soil-foundation interaction. It is very important to study soil behavior against the external loads. Soil behavior depends on many factors such as moisture content, density, particle-forming mineral types, grain size, grain shape, grading curve, current state of the stress, stress history, pore pressure, saturation point, permeability rate, time, and temperature. In order to study the soil-foundation interaction, many researchers have tried to investigate soil behavior against the imposed loadings to find a model for it. The material model is a mathematical relation for describing the stress-strain behaviour of a small element of the environment.
As previously mentioned, soil behavior depends on many factors it is extremely difficult to provide a model including the effects of all factors. Thus in solving the problems of soil-foundation interaction, some properties of the soil are usually excluded to provide a simpler model with fewer parameters. Since the soil at a macroscopic scale is considered as a continuum, the simplest possible state we consider the soil as a linear, homogenous and consistent elastic semi-space. In such a case, the soil will have two parameters Poisson coefficient and the elastic modulus. The first and simplest model for investigating the soil and foundation interaction is a model offered by Winkler in 1867 [10]. In this model, the deformation of any point of the soil ground is related to the point stress value and the effect of the stresses and the changes in other points are neglected. In this model, soil is replaced with a set of independent springs with a specific stiffness coefficient. Thus, only one single parameter is considered for the soil, that is, the subgrade reaction coefficient represented by ks. One of the most prominent properties of this model is its discontinuous behavior [9]. The subgrade modulus is not a fundamental soil property and its magnitude depends on many factors including the shape of the foundation, the stiffness of the foundation slab, the shape of the loading on the foundation, the depth of the loaded area below the ground surface, and the time. As such, it is not constant for a given type of soil, making the estimation of a single general value for design a challenging task [11]. Consequently, researchers have suggested several ways to determine this parameter and several formulae have been offered for determining ks.
Many researchers have worked on the calculation of subgrade reaction coefficient. Ismail [12] studied the applications of the artificial neural networks (ANN) and the simple-multiple regression analysis to predict the deformation modulus and the coefficient of the subgrade reaction of the compacted soils from the compaction parameters (such as maximum dry density (MDD) optimum moisture content (OMC), field dry density (FDD), and field moisture content (FMC)). Ding [13] compared four typical methods for determining the coefficient of the subgrade reaction including the test method, Lis method, MIDAS method, and finite element method. He showed that the test method is the one preferred by the designers, that the tangential coefficient should be in a range of one to two-third of the normal coefficient. The internal force of subway structures can be obtained by the test method and modified by a correction factor that is 1.05. Barmenkova et al. [14] carried out calculations of plates on an elastic basis with variable and constant coefficients of subgrade reaction. In this paper, the calculation of plates bending was carried out by the finite element method. The results were compared for different models of plates on an elastic basis. For a two-layer plate on an elastic basis, which had heterogeneity in the plan, the results of calculation took into account the increase of the height of the upper structure.
Kobayashi et al. [15] calculated the subgrade reaction coefficient for a foundation soil in an open pier using an extended Kalman filter (EKF) based on measurements taken during in situ horizontal loading tests on a pile. The numerical results would provide useful information for the future design of open piers and their foundations. Liao [16] reviewed the limitations of various simple and complex methods available for estimating the coefficient of subgrade reaction k, and developed a new method using the results of the plane strain finite element analyses of a loaded beam or slab resting on the surface of a homogeneous elastic soil layer.
Although many studies have been carried out on determining the subgrade reaction coefficient, the dependence on many parameters leads to further parametric studies. Experimental and theoretical formulas for determining ks are based on available data from limited sites with some assumptions, so it is possible for them not to have sufficient precision in all areas. Therefore, determining the subgrade reaction coefficient in specific areas such as Bandar Abbas city and assessment of the effective parameters on subgrade reaction coefficient is vital. Besides, the Increasing in footing width, increases effective depth. Therefore, determination of ks in footing with more width is more complex especially in layered soil, because ks obtained from plate load test is different from ks under real loading of structure. Thus investigation of the footing width and the strength parameters of the soil on ks is needed. Performing plate load tests with large diameters is expensive and difficult, thus the present study uses finite element software of Plaxis to investigate the effect of the aforementioned parameters.
Parametric studies on subgrade reaction coefficient of sand soil in Bandar Abbas city are few, so this paper uses geotechnical data of a site in Bandar Abbas city (Iran) to determine subgrade reaction coefficient by using of theoretical, experimental relations and numerical methods. Besides, the effects of the strength parameters (c,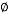 ) and B on subgrade reaction coefficient are investigated too. This study is carried out by using and verifying numerical methods and ensuring the accuracy of the software. Numerical analysis has been done by finite element method using Plaxis software [17].
) and B on subgrade reaction coefficient are investigated too. This study is carried out by using and verifying numerical methods and ensuring the accuracy of the software. Numerical analysis has been done by finite element method using Plaxis software [17].
- Analytical methods of subgrades reaction coefficient
In order to obtain ks, one can generally apply plate loading, consolidation, triaxial, and CBR tests and experimental and theoretic relations provided by researchers [18]. Among them, plate loading testing and the experimental method are considered the most common methods. In this paper, experimental and theoretic methods are considered. There are several relations including Vesic [19], Biot [20], and Bowles [6] as well as relations resulting from elastic theory from elasticity theory to determine subgrade reaction coefficient.
Biot [20] solved the problem of an infinite beam on a linear elastic subgrade and provided Eq. (1) for subgrade reaction coefficient.
|
(1) |
|
Vesic [19] developed Biot’s work [20] and suggested Eq. (2) for the relation between ks and elastic characteristic of soil:
|
(2) |
|
He also showed the difference between Winkler method and continuum does not exceed 10 percent. Bowles [6] showed the numerical value of 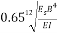 in ordinary condition may be approximated by 1, and in most cases subgrade reaction coefficient is obtained by Eq. (3):
in ordinary condition may be approximated by 1, and in most cases subgrade reaction coefficient is obtained by Eq. (3):
|
(3) |
|
Using elasticity theory is another way to approximate ks. By reformulating the elastic subsidence in rectangular foundation, we obtain the following [21]:
|
(4) |
|
These values are determined based on tables in the elastic subsidence section of basic soil mechanic references. “m” is the coefficient which is equal to 1, 2 and 4 for corner, edge, and center, respectively. ks is calculated in corners assuming m = 1 from Eq. (4) and it is multiplied by 0.5 to obtain k edges or by 0.25 to obtain ks centers. According to the above discussion, it can be seen that there are several formulae to determine soil subgrade reaction coefficient.
- General and geotechnical properties of the soil
The site of the residential- mercantile building is located to the west part of Bandar Abbas city in Iran (Fig. 1) with seven floors over the ground floor (parking lot). The depth of the foundation settlement is equal to the height of the foundation as 1 meter and no groundwater grade was observed until the end of the excavation depth. In order to identify the underground layers, five boreholes were excavated (three 15-meter boreholes and two 20-meter boreholes) using a rotary drilling machine. During soil boring, some samples were extracted for laboratory experiments. After completion of the field operation, the extracted samples were tested for grading, Atterberg limits, moisture content of the natural soil, and direct shear test. The studies on the layers of the site soil show the soil type in the foundation subgrade is mainly silty sand (SM) from the ground level down to the depth of 8 meters, and the soil type is bad-grained sand (SP) from the depth of 8 meters downwards.
Fig. 1. Location of Bandar Abbas city.
Considering the field and laboratory experiments in order to determine the scale of soil subsidence and the bearing capacity of the site soil, the required parameters were selected from the five excavated boreholes as shown in Table 1. The data of the samplings is available down to 20 meters deep. The soil type was given down to the depth of the foundation effect (around 30m). Moreover, the soil weight at the 20 to 30 m depth (layer 11) has considered as being constant.
Table 1. Soil properties of the site
|
No. of Layers |
Dep. (m) |
Soil Type |
SPT (Ncor.) |
ω (%) |
c (kPa) |
φ (˚) |
γ (kN/m3) |
γd(kN/m3) |
|
1 |
0-2 |
SM |
21 |
4.1 |
0 |
29 |
17 |
16.3 |
|
2 |
2-4 |
SM |
17 |
16.6 |
0 |
29.1 |
18.6 |
16.23 |
|
3 |
4-6 |
SM |
24 |
14.9 |
0 |
28.8 |
18.6 |
16.18 |
|
4 |
6-8 |
SM |
33 |
15.2 |
0 |
30.4 |
18.9 |
16.4 |
|
5 |
8-10 |
SP |
38 |
23.7 |
0 |
32.4 |
20.1 |
16.24 |
|
6 |
10-12 |
SP |
39 |
18.1 |
0 |
31.2 |
19.4 |
16.42 |
|
7 |
12-14 |
SP |
47 |
24.2 |
0 |
31.2 |
20.6 |
16.58 |
|
8 |
14-16 |
SP |
50 |
19.8 |
0 |
30 |
20 |
16.69 |
|
9 |
16-18 |
SP |
50 |
19.2 |
0 |
32 |
20 |
16.77 |
|
10 |
18-20 |
SP |
50 |
18.8 |
0 |
32 |
20 |
16.83 |
|
11 |
20-30 |
SP |
50 |
18.8 |
0 |
32 |
20 |
16.83 |
Equations (5) and (6) were used to determine the elasticity modulus of the soil [6]:
|
|
(5) |
For unsaturated sands, and
|
|
(6) |
For saturated sands.
Thus, the elasticity modulus for each of the soil layers is calculated based on the above formulae and the results are shown in Table 2.
Table 2. Elasticity modulus of the soil layers
|
No. of Layers |
SPT (Ncor.) |
Es (kPa)-dry |
|
1 |
21 |
18000 |
|
2 |
17 |
16000 |
|
3 |
24 |
19500 |
|
4 |
33 |
24000 |
|
5 |
38 |
26500 |
|
6 |
39 |
27000 |
|
7 |
47 |
31000 |
|
8 |
50 |
32500 |
|
9 |
50 |
32500 |
|
10 |
50 |
32500 |
|
11 |
50 |
32500 |
- Numerical analysis procedure
First, the results of Brian Anderson et al. [22] were analyzed with Plaxis to verify the software. Brian Anderson et al. [22] performed in situ testing and numerical investigation for predicting settlement of shallow foundations. Accordingly, a 1.8 m diameter concrete footing was statically load tested. Prior to construction, in situ standard penetration test (SPT), cone penetration testing (CPT), dilatometer (DMT), and pressuremeter (PMT) and laboratory tests were performed to determine engineering properties of the soil. A reinforced circular 1.8 m diameter 0.6 m thick concrete footing was constructed using a corrugated pipe coupler as a form. To overcome a thin hard layer surface crust, the footing was embedded 0.6 m into the ground. The groundwater table was at 1.7 m from the ground surface, as illustrated in Fig. 2. Static load was 222 kPa. Due to the symmetry, half of footing with the width of 0.5 B is modeled asymmetrically. Avoiding boundary effects, a 6.5Ã-5 m model was selected. The model depth was taken as 6.5 m, that is approximately equal to 4B=6.8 m and the width of the model was taken as 5 m, that is approximately equal to 3B [23] . Results proved that the displacement did not reach the boundaries in the analysis. To investigate the mesh dependency, a number of trial analyses were conducted through the verification study. The model included 1971 nodes and 235 elements. The boundary lines were defined as the limited deformation in horizontal direction and free deformation in vertical direction, and limited deformations both in horizontal and vertical directions at the lower boundary as showed in Fig. 3. Trial analyses proved that with specified dimension and meshing, errors would be negligible. In order to do the modeling with finite element method, the 15-node triangular element was used according to Fig. 4. Table 3 presents the input parameters used for the FEM analyses. Figure 5 presents applied stress-settlement diagram obtained from Plaxis in this study and reference to a point located under plate. There was a negligible difference between two diagrams, so Plaxis was suitable for analysis.
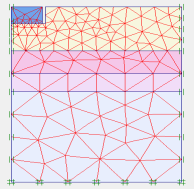
Fig. 2. Geometry and mesh of the verification model.
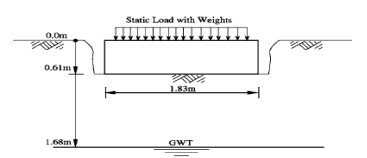
Fig. 3. Soil-footing profile of verification model [22].
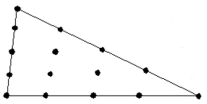
Fig. 4. 15-node triangular element.
Table 3. Soil properties used in verification according to [22].
|
Bottom(m) |
|
|
E(Mpa) |
c(kPa) |
|
1.64 |
18.9 |
31.4 |
14.5 |
0 |
|
2.5 |
17.3 |
30.1 |
12.5 |
0 |
|
3.17 |
15.7 |
28.6 |
10.50 |
0 |
|
6.5 |
14.2 |
27.1 |
8.5 |
0 |
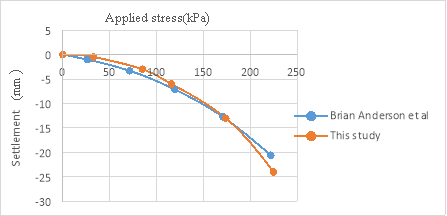
Fig. 5. Applied stress-settlement diagram.
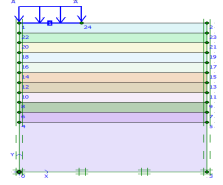
After software verification, the model was developed for determining the subgrade reaction coefficient of Bandar Abbas city and parametric study. In the created model (which included 2011 nodes and 256 elements), the loading was uniform and, a rigid foundation was considered in all phases of analysis. Model depth should be greater than 4B and model width greater than 3B for different diameters. Since it was intended to study the effect of foundation diameter on determining the value of subgrade reaction coefficient, an asymmetric model was used in the software for soil modeling. The relevant parameters of the general properties (wet and dry specific weight) and the relevant parameters of the soil resistance (c,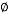 ) for all soil layers were derived from Table 1. Considering the results of the experiments and researches and the reliability of the developed numerical model with the results, and considering the soil type of the site (sand soil), Mohr-Coulomb behavioral model for the soil was used in this research. Since in Mohr-Coulomb behavioral model the stress-strain relation is fulfilled directly by the soil elasticity coefficient, thus in entering the data of the soil elasticity coefficient as one of the input parameters, the data of Table 2 were used. The values of the dilation angle in all layers were assumed to be 0. Considering the properties of the building in this project and the scale of the imposed loading (dead and live load), the value of the imposed pressure on the soil was assumed to be 120 kN/m2 where the plate element (with the concrete foundation properties) was used to transfer this load to the modeled soil. Among the most important properties of the element, it could be referred to its flexural hardness (EI) and its axis hardness (EA). These two parameters can be used to obtain the plate thickness that is the representative of the foundation thickness in this case. Considering the constant thickness of the foundation by 1 meter in this research, different values would be obtained for EI and EA in different models according to the Eqs. (7) and (8) [24]. Since the modeling was done with asymmetric method, thus half of the diameter of the real foundation was modeled, and the modeling was done in direction of x-axis, three times more than the foundations diameter (3B), and in the direction of y-axis equal to the number of the layers mentioned in Table 1. Moreover, Table 4 shows the parameters needed for determining the plate input parameters into Plaxis software.
) for all soil layers were derived from Table 1. Considering the results of the experiments and researches and the reliability of the developed numerical model with the results, and considering the soil type of the site (sand soil), Mohr-Coulomb behavioral model for the soil was used in this research. Since in Mohr-Coulomb behavioral model the stress-strain relation is fulfilled directly by the soil elasticity coefficient, thus in entering the data of the soil elasticity coefficient as one of the input parameters, the data of Table 2 were used. The values of the dilation angle in all layers were assumed to be 0. Considering the properties of the building in this project and the scale of the imposed loading (dead and live load), the value of the imposed pressure on the soil was assumed to be 120 kN/m2 where the plate element (with the concrete foundation properties) was used to transfer this load to the modeled soil. Among the most important properties of the element, it could be referred to its flexural hardness (EI) and its axis hardness (EA). These two parameters can be used to obtain the plate thickness that is the representative of the foundation thickness in this case. Considering the constant thickness of the foundation by 1 meter in this research, different values would be obtained for EI and EA in different models according to the Eqs. (7) and (8) [24]. Since the modeling was done with asymmetric method, thus half of the diameter of the real foundation was modeled, and the modeling was done in direction of x-axis, three times more than the foundations diameter (3B), and in the direction of y-axis equal to the number of the layers mentioned in Table 1. Moreover, Table 4 shows the parameters needed for determining the plate input parameters into Plaxis software.
|
d= ½ deq |
(7) |
|
|
(8) |
|
|
|
Fig. 6. Geometry of the model. |
|
Table 4. Plate parameters |
|||
|
EI (kNm2/m) |
EA (kN/m) |
E (kPa) |
Df(m) |
|
Var. |
Var. |
2.5Ã-107 |
1 |
- Results and discussion
Seven models were developed for different values of foundation diameter (8, 10, 12, 14, 16, 18, and 20 m). Then, they were analyzed by finite element method using Plaxis. Because of axis plain strain in Plaxis, foundation is considered as a strip with B/2 of diameter and 1 m, orthogonal to the plane as shown in Fig. 6. Amount of vertical displacement in center and below of the foundation (sections are in center and 1 meter below the above subgrade of soil model) is obtained according to the load determined by the construction analysis (120 kN/m2). The soil subgrade reaction coefficient is calculated by Eq. (9) for any values of foundation diameter [25]:
|
(9) |
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal
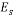
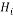

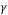
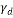
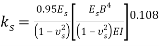
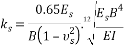
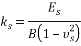
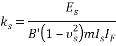
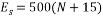
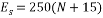
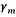 (kN/m3)
(kN/m3)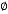 (deg)
(deg)