Impact of Seismicity on Performance of RC Shear Wall

Impact of Seismicity on Performance and Cost of RC Shear Wall Buildings in Dubai, UAE

Mohammad AlHamaydeh, P.E., M.ASCE [1]; Nader Aly, S.M.ASCE [2]; and Khaled Galal, P.Eng., M.ASCE [3]

ABSTRACT

Unfortunately, available probabilistic seismic hazard studies are reporting significantly varying estimates for Dubai seismicity. Given Dubai’s rapid economic growth, it is crucial to assess the impact of the diverse estimates on performance and cost of buildings. This research investigates and quantifies the impact of the high and moderate seismicity estimates of Dubai on the seismic performance, construction and repair costs of buildings with 6, 9 and 12 stories. The reference buildings are made up of reinforced concrete with special shear walls as their seismic force resisting system. The seismic performance is investigated using nonlinear static and incremental dynamic analyses. Construction and repair costs associated with earthquake damages are evaluated to quantify the impacts. Results showed that designing for higher seismicity yields significant enhancement in overall structural performance. In addition, the higher seismicity estimate resulted in slight increase in initial construction cost. However, the increase in initial investment is outweighed by significant enhancements in seismic performance and reduction in earthquake damages. This resulted in overall cost savings when reduction in repair and downtime costs are considered.

Keywords: Seismic Hazard, RC Shear Walls, Seismic Vulnerability, Seismic Performance, Earthquake Losses.

Introduction and Background

The economy of UAE and specifically Dubai has been rapidly growing over the past few decades. Significant investments are taking place in the various sectors, especially in the real estate sector. In addition, in November 2014, Dubai was announced to be the hosting city of the coming EXPO 2020. As a result, substantial growth is taking place in the real estate sector. Several residential, commercial and hotel buildings are going to be designed and constructed to accommodate the increase in population size. This region suffers from considerable uncertainty in its seismicity level and the design guidelines that should be followed (AlHamaydeh et al., 2012). The seismicity level of UAE and Dubai has been the matter of several research studies, such as Abdalla and Al-homoud (2004), Aldama-Bustos et al. (2009) and Khan et al. (2013). Nevertheless, unfortunately there is not much consensus in these research studies about the seismicity levels that should be designed for in UAE. This could be attributed to the lack of in-depth seismological data and historical recordings of ground motions in this region. Such data would have been useful in providing comprehensive and sound seismic design guidelines (AlHamaydeh et al., 2013). The minimum seismic design requirements set by the local authorities in Dubai are based on the 1997 Uniform Building Code (UBC’97). However, the municipality has been proactive in adapting to tremors that were felt and measured in UAE in April, 2013. They sent a circular to consulting offices in May, 2013 raising the minimum requirement to zone 2B for buildings higher than nine stories and zone 2A for buildings between four to nine stories. Therefore, the unprecedented growth in the number of buildings in Dubai combined with the lack of consensus on seismic design criteria complicate the vulnerability to earthquakes. It is generally believed that the UAE has low seismicity. Nevertheless, over the past few years, a significant number of regional seismic activities, originating from faults surrounding the UAE, has been recorded by Dubai Seismic Network (DSN). Additionally, DSN has recorded some local seismic activities over the period from 2006 to 2014.

UAE seismicity is affected by earthquakes originating from near-fault and far-field seismic sources (Mwafy, 2011). The most recent seismic hazard study for UAE, available to the authors, was published in 2013 by Khan et al. (2013). The study provided a comprehensive probabilistic seismic hazard assessment and spectral accelerations for the entire UAE. Furthermore, it implemented a standardized earthquakes catalogue for UAE compiled from United States Geological Survey (USGS), National Geosciences of Iran (2015) and the National Center of Meteorology and Seismology of UAE (NCMS) (2015) that dates back to 110 years. Furthermore, Khan et al. (2013) have used seven different ground motion prediction equations incorporating three next generation attenuation equations due to the lack of specific equations for UAE. They attributed UAE seismicity to the seismic source zones shown in Figure 1. In addition, the seismic hazard study by Shama in 2011 highlighted several local crustal faults in UAE that might affect its seismicity level. These faults are Dibba, Wadi El Fay, Wadi Ham, Wadi-Shimal, Oman and West Coast fault (Shama, 2011). Unfortunately, the level of seismicity is not clearly set since there is no strong consensus among researchers about the exact seismic level of UAE or Dubai. On the other hand, reviewing the available probabilistic seismic hazard studies conducted for UAE and Dubai clearly shows that there are significant variations in the estimated seismicity levels. In fact, results vary from no seismic hazard to very high seismicity. Table 1 shows a summary of Peak Ground Accelerations (PGA) from several probabilistic seismic hazard studies. The reported PGAs vary from less than 0.05g to 0.32g. This is attributed to the differences in the used source zonation, recurrence parameters, earthquake catalogues and ground motion prediction equations. The differences are mainly due to the lack of detailed seismological measurement and data in this region and such data is required to provide a comprehensive and sound seismic hazard study (AlHamaydeh et al., 2013). The variation in seismicity was a driving factor for many research studies related to the impact on design of buildings in Dubai, such as (AlHamaydeh et al., 2010; AlHamaydeh et al., 2011; and AlHamaydeh and Al-Shamsi, 2013).

The objective of this paper is to investigate the impact of the seismicity hazard level on the performance, construction, repair and downtime costs of reinforced concrete (RC) shear wall buildings in Dubai. In this regard, six RC shear wall buildings are designed and detailed following the 2012 International Building Code (IBC’12) standards. The reference buildings are 6-story, 9-story and 12-story. They are chosen to target the main sectors of buildings inventory in Dubai, UAE. These buildings are designed for two different seismic hazard levels that represent high and moderate seismicity estimates of Dubai. The different designs are compared based on their seismic performance, construction and repair costs in order to investigate and quantify the impact of the seismic design level. The seismic performance is evaluated following the methodology outlined in FEMA P695, which is a technical publication aiming to establish standard procedures for quantifying the seismic performance factors of buildings (Federal Emergency Management Agency (FEMA), 2009). The assessment methodology is based on nonlinear pseudo-static and dynamic analyses. The nonlinear response history analyses are performed using a set of ground motion records selected and scaled to represent the highest possible seismic activity in Dubai. As such, this would highlight the implications on design, seismic performance, construction and repair costs of RC shear wall buildings designed for different seismic hazard levels in Dubai, if the high seismicity estimate turns to be the most realistic. In addition, total construction cost is estimated considering structural and non-structural components. Finally, the repair cost is evaluated based on the structural and non-structural damage percentages adapted from SEAOC blue book (Structural Engineers Association of California, 1999).

Details of the Reference Buildings

The six reference buildings considered in this paper are intended to represent typical office buildings located in Dubai, UAE. The buildings have number of floors ranging from 6 to 12 stories to represent the majority of common buildings in Dubai. They are made up of RC and have a typical floor plan as shown in Figure 2. The plan consists of five 6m (20ft) bays and total dimensions of 30mx30m (100ftx100ft). Furthermore, the overall structural height varies between 24m to 48m (78ft to 156ft); with a typical floor height of 4m (13ft). The lateral force resisting system consists of special RC shear wall placed along the perimeter of the building. This arrangement ensures that center of mass is close to center of rigidity, hence it avoids inherent torsional effects. In addition, placing the walls along the perimeter boosts the building torsional resistance and reduces the shear demands on walls due to accidental torsion effects.

The gravity system consists of RC square columns, while the floor system comprises of cast-in-situ flat plate. However, the gravity system is not designed to be part of the lateral force resisting system. It is only designed to support vertical loads and to satisfy the deformation compatibility requirement. For design purposes, concrete compressive strength (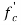) is assumed to be 28MPa (4.0ksi) for columns and slabs, and 38MPa (5.0ksi) for shear walls. Additionally, the yield strength (f_y) of reinforcement is assumed to be 420MPa (60ksi). Super Imposed Dead Load (SDL) is 3.6kPa (75psf), excluding the self-weight of the concrete slabs. This SDL value is a conservative estimate commonly used for office buildings in Dubai. The breakdown of this estimate is as follows: 2 kPa (for 100mm of leveling screed and flooring tiles), 1 kPa for partitions (usually movable partitions) and 0.6 kPa allowance for mechanical, electrical and plumping overhanging services. Curtain wall (cladding) load on the perimeter of each floor is 0.72kPa (15psf). Moreover, for office buildings the typical floors live load is 2.4kPa (50psf) and the roof live load is 1kPa (20psf) as per ASCE7-10.

The six reference buildings are designed and detailed according to IBC’12 requirements for two different seismic hazard levels representing high and moderate seismicity estimates in Dubai. The selection of the two seismic design levels is driven by the existing uncertainty in seismic loading and the substantial variability in reported seismic hazard levels for UAE and Dubai. Therefore, it is deemed a reasonable choice for the objective of this paper to consider the highest and moderate seismicity levels. This would allow investigating the consequences of the possible alternative seismic loading levels available to designers. The highest seismicity level represents the upper bound, and it is obtained from USGS (2015). The USGS seismic hazard level for Dubai estimate is selected in this study (i.e. S_s = 1.65g and S₁ = 0.65g). Moreover, the moderate seismic design level represents Abu Dhabi International Building Code 2011 (ADIBC’11) estimate for Dubai. The elastic design response spectra for the two considered seismicity levels along with the ASCE7-10 estimated fundamental periods of the studied six buildings are presented in Figure 3. As shown, at each seismic design level, three buildings with 6-stories, 9-stories and 12-stories are designed with special RC shear walls. Summary of all buildings’ details including response modification factors (R and C_d), design spectral accelerations and elastic fundamental time periods, and approximate periods’ upper limit are given in Table 2. It is worth mentioning that the ground motion input parameters (S_s and S₁) of the two seismicity levels (high and moderate) result in Seismic Design Category (SDC) D for the six considered buildings. Consequently, ordinary RC shear walls are not permitted by the design code (i.e. ASCE7-10). Thus, all buildings are required to have special RC walls. Furthermore, choosing special detailing for both seismicity levels would allow investigating the direct impact of the seismic design level on the cost and performance of walls with same level of detailing requirements. The buildings are given a legend showing its ID (i.e. Building1 to Building6), number of stories (i.e. 6Story, 9Story or 12Story), seismic design level (i.e. High or Moderate) and shear wall type (i.e. Special or Ordinary). A site class D is assumed for the six reference buildings. This assumption complies with IBC’12 recommendations.

Design Summary

The buildings are designed and detailed in accordance to IBC’12 standards which refers to ASCE7-10 for minimum design loads and ACI318-11for structural concrete requirements. The designs implement the state of the art practices in design and construction followed in Dubai, UAE. For the design purposes, elastic analysis is done using 3D models on CSI ETABS commercial package (“ETABS,” 2015). To determine the majority of the seismic mass, the gravity system is designed first and fixed for the three buildings.

The gravity system is designed to resist axial forces from all vertical loads in addition to the moments and shears induced from deformation compatibility requirements. In order to ensure the structural stability of gravity columns, they are designed to resist the induced actions (bending moments and shear forces) from the deformations that will be imposed by earthquake excitations on the building. The bending moments and shear forces are estimated based on the maximum allowable inter-story drift by IBC’12 which is 2%. The stiffness of the columns is estimated using ETABS by applying a force at the top and bottom of the considered story and by getting the corresponding displacement. The shear forces are then calculated by multiplying the maximum allowable displacement by the stiffness of each column. Then from the shear force, the moment is calculated as shown in Equations (1) and (2).

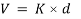(1)

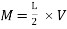(2)

Where V is shear force, d is displacement (calculated using ETABS), M is bending moment and L is column height. It should be noted that concrete shear capacity is found sufficient to resist the shear forces due to imposed deformations by applied seismic forces. Therefore, minimum lateral reinforcement (i.e. column ties) is provided in columns with reference to clause 7.10 in ACI318-11. The gravity system components (i.e. flat plates and columns) are designed in accordance to ACI318-11 provisions using in-house design spreadsheets. For an optimized design, following common design trends in UAE, columns cross sections and reinforcement are grouped and changed every three floors. The gravity system is common between buildings with the same number of floors. The gravity columns design details for the six reference buildings are summarized in Figure 4. Figure 4 (a), (b) and (c) show the dimensions and reinforcement details of the 6- , 9- and 12-story buildings, respectively. On the left side of each Figure, the columns’ cross section dimensions are provided over each group of floors. The right side shows the vertical and horizontal reinforcement of the different columns (i.e. columns around the opening and remaining columns) in each group of floors. The minimum required slab thickness is calculated such that it satisfies ACI318-11 Table 9.5(c) minimum requirements. For the longest clear span of 5.3m, the minimum required thickness is 177mm. This figure is rounded up and 200mm thick flat plates are used. The flat plates are reinforced with T16 reinforcement bars spaced at 125mm, top and bottom in both directions. Additional T20 reinforcement spaced at 125mm (2m long) are added on top of columns in both directions.

The lateral system is designed to resist the seismic lateral loads determined according to IBC’12 Static Equivalent Lateral Force (SELF) method. The SELF method is permitted for all the six reference buildings. This is because the total height for all buildings does not exceed 48m (160ft), the SDC is D and no structural irregularities exist according to ASCE7-10, Table 12.6-1. Linear static analysis is performed using ETABS to evaluate the induced forces and displacements from seismic forces. Then, shear walls are designed to satisfy strength and drift requirements. Inter-story drift ratios are controlled within code, IBC’12, limits (2%) by varying the shear wall stiffness through changing its in-plan length. Strength requirements are satisfied by designing the shear walls for the induced bending moments and shear forces by the seismic actions using Quickwall software (“Quick Concrete Wall,” 2015). Shear walls’ thickness and reinforcement are changed every three floors to optimize the design and to match common design practices in Dubai. However, walls’ in-plane length is kept constant throughout the buildings height to avoid any vertical structural irregularities. The need for specially detailed boundary elements is checked every three floors using the displacement-based approach. The use of displacement based approach for checking the boundary elements vertical extent is preferred over the use of stress-based approach. This is because the latter approach was proven to provide highly conservative requirements for the special detailing (Wallace and Moehle, 1992) and (Thomsen IV and Wallace, 2004). For practical constructability, boundary elements are designed to have the same wall thickness. Additionally, to comply with ACI318-11 minimum thickness requirements and conform to typical design practices in the UAE, an aspect ratio of at least 25.4mm: 304.8mm (1in: 12in) is maintained between wall thickness and length. The walls’ minimum thickness depends on the unsupported height and length. Therefore, as the walls’ unsupported heights across the different buildings are constant (i.e. limited by the typical story height), it is necessary to impose a practical criterion on the walls’ thickness as we change the length from building to building. This approach guarantees that the different designs are subjected to the same guidelines, especially for sizing the walls’ cross sections. This would result in a fair response comparison among all designs as they follow similar basis that imitates typical design practices in the UAE. During initial dynamic analyses of the 12-story buildings, B5-12S-H-S and B6-12S-M-S, it was observed that the critical section was not at the walls’ base. This is contradicting the code assumption of having a single critical section at the base of cantilevered shear walls. The critical section resulting in the dynamic analysis was actually shifted from the wall base to the bottom of the lowest floor in upper quarter of the building (10^th floor). The initiated failure mechanism was governed by higher modes effects and the formation of plastic hinges at upper floors. The optimization done initially to the design by reducing dimensions and reinforcement for upper floors magnified the impact of higher modes effects. As a result, it triggered the failure and plastic hinge formation to be initiated at the reduced cross section. Therefore, the critical section became located at the weak spot at higher levels, which resulted in an unfavorable premature collapse mechanism. This observation has been highlighted by previous researchers, such as Tremblay et al. (2001), Bachmann and Linde (1995), and Panneton et al. (2006). It was also experimentally proven by shake table and cyclic loading tests (El-Sokkary et al., 2013). As an example, the modal analysis of the 12-story building, B5-12S-H-S, is shown in Table 3. It can be seen that there are clear separations between the individual modes’ characteristics (periods and modal masses). This is generally expected in a flexural cantilever structural type (i.e. shear walls). The first mode effective mass is usually ranging from 50% to 70% and the second mode period is approximately one sixth of the first mode. This is consistent with many research studies which investigated the effects of higher modes on response of cantilever shear walls (e.g. Humar and Mahgoub, 2003 and Tremblay et al., 2001). Furthermore, it is clear that relative modal weights (%) and modal participation factors are relatively high at 7^th, 8^th and 12^th vibration modes which highlights the impact of higher modes. As a result, the design was revised by keeping the cross section and reinforcement constant for the upper half of the 12-story (B5-12S-H-S and B6-12S-M-S) and 9-story buildings (B3-9S-H-S and B4-9S-M-S). For 6-story buildings (B1-6S-H-S and B2-6S-M-S), a single cross-section was used for all floors with terminating boundary element at third floor. This conforms to the state-of-art design and construction practices in Dubai, UAE. It also matches the design philosophy adopted in other 12-story and 9-story buildings by keeping the same cross section and reinforcement for upper six floors. Summary of the shear walls design details is shown in Figure 5.

Nonlinear Modeling

The six reference buildings are modeled using lumped plasticity formulations on IDARC-2D (Reinhorn et al., 2009). Since the buildings are symmetric, mass participation of torsional modes of vibration are low. Therefore, torsional effects are negligible and a two-dimensional model is sufficient to simulate the buildings’ response. The shear walls are idealized using macro-models by representing the structural members with equivalent elements possessing all nonlinear characteristics. The members’ nonlinear characteristics depend on distribution of plasticity and yield penetration. A lumped plasticity model consisting of two nonlinear rotational springs located at the ends and an elastic member is used for the shear walls. The nonlinearity is concentrated at the locations of the nonlinear rotational springs. The flexural and shear deformations of the shear walls are modelled using the tri-linear (three parameter) hysteretic model developed by Park et al. (1987). The tri-linear hysteretic models allow controlling the stiffness degradation and strength deterioration due to ductility and energy. In addition, the axial deformations of the shear walls are considered by a linear-elastic spring. For the shear walls, the moment-curvature and shear-distortion are calculated using the fiber elements procedure of IDARC2D. The wall cross section is divided into number of fibers and then subjected to increments of curvatures. From strain compatibility and equilibrium, the strains are calculated and used to compute the resulting axial forces and bending moments in the section (Reinhorn et al., 2009).

Results and Discussion

The buildings’ seismic performance is evaluated following FEMA P695 methodology (2009). FEMA P695 approach is based on nonlinear pseudo static (pushover) analysis, Incremental Dynamic Analysis (IDA) and fragility analysis. Pushover analysis is used to validate the nonlinear model and estimate the period based ductility of the buildings. Then, IDA analysis is performed using a suite of far-field ground motion records to estimate the median collapse intensity and collapse margin ratio. The far-field ground motion records are scaled to match the MCE response spectrum of the highest seismicity estimate in UAE. This seismicity hazard level is as estimated by USGS (2015) for Dubai (S_s = 1.65 g and S₁ = 0.65 g). The selected scaling level simulates the worst, yet possible seismic hazard scenario from distant sources (e.g. Zagros thrust or Makran subduction zone) as highlighted by Sigbjornsson and Elnashai (2006). Thus, it allows assessing the consequences of the selected seismic design level (i.e. high or moderate) on the seismic performance, construction and repair costs of RC shear wall buildings in Dubai. The calculated collapse margin ratios from the IDA are adjusted to account for uncertainties in design basis, test data, nonlinear modeling and to consider the spectral shape of the ground motion records. The spectral content is accounted for based on the calculated period based ductility. Adjusted IDA results are finally used to calculate exceedance probabilities for ASCE-41 (2013) performance levels, Collapse Prevention (CP), Life Safety (LS) and Immediate Occupancy (IO).

Nonlinear Pseudo-Static (Pushover) Analysis

Pushover analysis is performed using an inverted triangle displacement profile as a pushing function for all buildings. The intensity is increased monotonically until the ultimate base shear degrades by 20%. The results are used to construct capacity curves (back-bone) for the reference buildings in the form of roof drift ratio versus base shear coefficient (i.e. base shear normalized by seismic weight). Pushover capacity curves are used to assess the buildings deformation and strength capacities.

The capacity curves of the three buildings designed for the high seismicity estimate (i.e. B1-6S-H-S, B3-9S-H-S and B5-12S-H-S) are shown in Figure 6. Normalized base shear capacities are 0.57, 0.5 and 0.46 for B1-6S-H-S, B3-9S-H-S and B5-12S-H-S, respectively. As expected, base shear capacity is higher for the shorter building (6-story). This is attributed to the higher design forces which resulted from the relatively higher initial stiffness of squat shear walls compared to their slender counterpart. B1-6S-H-S reached a maximum roof drift ratio, prior collapse, of 6.5%, while B3-9S-H-S reached 6% and B5-12S-H-S reached 7.25%. The three buildings have period-based ductility calculated as recommended by FEMA P695 greater than 8. It can also be observed that in the three high seismicity designs, the capacity curves do not experience severe degradation in strength or deterioration in stiffness. This matches the expected behavior of well detailed special RC shear walls with confined boundary elements. It is noticed from the final damage states of the buildings, at 20% strength degradation, that static pushover analysis resulted in a failure mode at the base of the shear walls conforming to the design code assumed critical section. The overall structural damage index reported by IDARC-2D is 0.359, 0.426 and 0.618 for B1-6S-H-S, B3-9S-H-S and B5-12S-H-S. It is worth mentioning that these damages are concentrated at first floor shear walls.

Established capacity curves for buildings designed for moderate seismicity (B2-6S-M-S, B4-9S-M-S and B6-12S-M-S) are presented in Figure 6. From shown capacity curves, normalized base shear capacities are 0.31, 0.26 and 0.24 for buildings B2-6S-M-S, B4-9S-M-S and B6-12S-M-S, respectively. Similar to the high seismicity design, the 6-story building has the highest normalized base shear capacity. This is due to its lateral system (shear walls) relatively higher stiffness which resulted in higher demands. Maximum drift ratios, prior collapse achieved by B2-6S-M-S, B4-9S-M-S and B6-12S-M-S are 9.25%, 8% and 3.5%, respectively. The three designs have period-based ductility greater than 8 calculated as recommended by FEMA P695. The overall structural damage index reported by IDARC-2D is 0.371 for B2-6S-M-S, 0.455 for B4-9S-M-S and 0.359 for B6-12S-M-S. These damages are triggered at the first floor shear walls only. Therefore, similar to high seismicity designs, the pseudo static pushover analysis results of moderate seismicity designs suggests a single critical section at the wall base. This conclusion matches with design code recommendation for regular buildings permitted to be designed following the static method (SELF) by ASCE7-10.

Nonlinear Incremental Dynamic Analysis (IDA)

The seismic performance of the reference buildings is investigated under the random nature of earthquakes. Standard nonlinear pseudo-static analysis does not inherently fully capture the higher modes effects which usually govern the response of tall and irregular buildings. Consequently, the use of nonlinear dynamic analysis is more appropriate in such cases. IDA provides better insight of the expected structural response from the linear range through the nonlinear response and until it losses stability and collapse (Vamvatsikos and Cornell, 2004). The IDA in this case is performed using a very fine increment of 0.1g for the spectral accelerations. The increments are increased until all ground motion records caused the buildings to collapse or exceed the CP maximum drift ratio limit of 2% as specified by ASCE-41. However, the maximum spectral acceleration for all the records is not increased more than 2.5g. The total number of dynamic analysis runs performed for each reference building is around 1100 (22 records x 2 components x 25 scale factors).

Figure 7 presents the resulting IDA curves for high seismicity designs, B1-6S-H-S, B3-9S-H-S and B5-12S-H-S. The structural response derived from IDA curves can depend to some extent on the characteristics of the particular accelerograms used. Thus, the performance is judged based on a suit of ground motion records to segregate this effect. On average, at low drift ratios (approximately up to 1%), the three designs (B1-6S-H-S, B3-9S-H-S and B5-12S-H-S) exhibit a linear behavior. The same linear behavior is resulting from some of the ground motion records up to the MCE spectral acceleration. At higher spectral accelerations, the structural response starts to vary showing several patterns of nonlinearities, such as softening, hardening and weaving. For only few records, the structure seems to soften and move to large drifts rapidly until it reaches collapse. Collapse in these curves, whether resulting from convergence issues, numerical instabilities, or very large drift ratio, is represented using a drift ratio of 10% and a flat line in IDA curves. Majority of the earthquake records caused severe hardening and weaving around the elastic response. The weaving observation conforms to the common equal displacement rule stating that inelastic and elastic displacements are equal for structures with relatively moderate time periods (Vamvatsikos and Cornell, 2002). In addition, for some records, the hardening phenomenon in which the structure seems to perform better at higher intensities is somewhat against the common expectation (Vamvatsikos and Cornell, 2002). This is because generally the time and pattern of the time-history governs the response more than just the intensity. Moreover, the upward scaling done to the records makes the less responsive cycles at the beginning of the time-history strong enough to cause damage and yielding of the structural elements. Therefore, some strong ground motion records at some intensity might cause early yielding of a specific floor, usually a low floor. This floor acts as a sacrificial fuse which reduces the response of higher floors (Vamvatsikos and Cornell, 2002). Another very interesting observation that is clearly seen in IDA curves shown in Figure 7 is what is called “Structural Resurrection.” This phenomenon has been observed by Vamvatsikos and Cornell (2002) and is defined as a severe hardening behavior. In structural resurrection, the building moves all the way to complete collapse (numerical instability or convergence issues) at some intensity. Then at higher intensities it shows a lower or higher response, but without collapsing. This happens because the time and pattern of the ground motion record at a particular intensity might be more damaging than at higher intensities. In other words, this particular intensity causes the stru