Fuzzy Logic Technique for Image Enhancement

Abstract– Now day’s applications should be require various types of images and pictures as sources of information for interpretation and analysis. Whenever an image is changed from one to another form such as, digitizing, scanning, transmitting and storing, some of the degradation always occurs at the output end. Hence, the output image has to go in a process called image enhancement which consists of a collection of techniques that need to improve the quality of an image. Image enhancement is basically improving image and its interpretation and perception of the information in digital images and providing good input for different other automated image processing techniques. The fuzzy set theory is always uncertainties (like it comes from the information available from situation such as darkness may result from incomplete, imprecise, and not fully reliable). The fuzzy logic gives a mathematical model for the representation and processing of good knowledge. The concept is depends upon if-then rules in approximation of the variables likes threshold point. Also the Uncertainties within image processing tasks often due to vagueness and ambiguity. A fuzzy technique works as to manage these problems effectively.

IndexTerms– Fuzzy Logic, Image Processing, Image Enhancement, Image Fuzzification, Image Defuzzification

Whenever an image is changed from one to another form such as, digitizing, scanning, transmitting and storing, some degradation is always occurs at the output stage. Hence, the output image has to go in a process called image enhancement. Image enhancement consists of a collection of techniques that need to improve the overall quality of an image. Fuzzy image processing is the approaches that understand, represent and process the images and their pixels with its values as fuzzy sets. The representation and processing is depending upon the selected fuzzy techniques and the problem to be solved. The idea of fuzzy sets is very simple and natural. For instance, if someone want to define a set of gray levels, one has to define a threshold for gray level from 0 to 100. Here 0 to 100 are element of this fuzzy set; the others do not belong to that set. The basis logic behind fuzzy technique is the basis for human communication. This observation depends upon many of the other statements about fuzzy logic. As fuzzy logic is built on the logics of qualitative description used in everyday language, fuzzy logic is very easy to use. A filtering system needs to be capable of reasoning with values and uncertain information; this suggests the use of fuzzy logic.

II. FUZZY IMAGE PROCESSING — OVERVIEW

Fuzzy image processing techniques is not unique theory. It is a collection of different fuzzy approaches to image processing techniques. The following definition is to be regarded to determine the boundaries of fuzzy digital image processing:

Fuzzy image processing is the approaches that understand, represent and process the digital images and their segments and also features as fuzzy sets. The representation of it and processing is always depending on the selected fuzzy techniques and on the problem which need to be solved [9]. Below a list of general observations is defined about fuzzy logic:

• Fuzzy logic is conceptually very easy to understand.

The mathematical concepts behind fuzzy logic reasoning are simple. Fuzzy logic is important approach without the far-reaching complexity.

• Fuzzy logic is flexible.

Everything is indefinite if you look closely enough, but more than that, most things are indefinite. Fuzzy reasoning prepared this understanding into the process rather than just theory.

• Fuzzy logic can model the nonlinear functions of mathematically complexity.

One can create a fuzzy logic system to compare any sets of input and output data. This process is very easy by some of the adaptive techniques such as Adaptive Neuro-Fuzzy Inference Systems, which is already available in Fuzzy Logic Toolbox.

• Fuzzy logic can be design on the top of experience of experts.

In case of neural networks, it must need training data and generate the outputs. But fuzzy logic will explain you about the experience of people who already understand the whole systems.

• Fuzzy logic can be mixed with any conventional control techniques.

Fuzzy systems don’t replace conventional control methods necessarily. Sometimes fuzzy systems increase them and simplify its implementation.

• Fuzzy logic is based on natural language communications.

The basis for fuzzy logic is the basis for human communication and this observation explain many of the other statements about fuzzy logic as well. Actually Fuzzy logic is built on the structures of quality description used in everyday languages used for communications. Fuzzy logic is very easy to use.

Natural language, which people used on a daily basis, has been comes by thousands of years of human history to be efficient. Sentences that are written in ordinary language always represent a triumph of efficient communication [3].

Fuzzy image processing has three stages: 1) Image Fuzzification 2) Modification of membership values 3) Image Defuzzification.

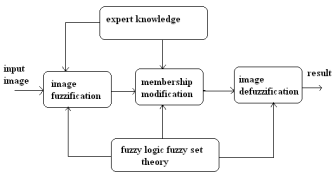
Figure 1. Basic Fuzzy Image processing [5]

The fuzzification and defuzzification steps are that in which we do not own fuzzy hardware. So, the coding of image data often called as fuzzification and decoding of the results called as defuzzification are the steps to process images with fuzzy techniques. The main thing of fuzzy image processing is in the intermediate stage that is modification of membership values (See Figure 1). After the image data are transformed from grey-level to the membership plane that is known as fuzzification is appropriate fuzzy techniques which modify the membership values which can be a fuzzy clustering and a fuzzy rule based approach and also it can be a fuzzy integration approach.

1. The Fuzzy set theory

Fuzzy set theory is the extension of crisp set theory. It works on the concept of partial truth (between 0 & 1). Completely true is 1 and completely false is 0. It was introduced by Prof. Lotfi A. Zadeh in 1965 as a mean to model the vagueness and ambiguity in complex systems [3].

2. Definition Fuzzy set

A fuzzy set is a pair (A, m) where A is a set and m: A-> [0, 1]. For each, x A m(x) is called the grade of membership of x in (A, m). For a finite set A = {x1,…,xn}, the fuzzy set (A, m) is denoted by {m(x1) / x1,…,m(xn) / xn}. Let x A Then x is called not included in the fuzzy set (A, m) if m(x) = 0, x is called fully included if m(x) = 1, and x is called fuzzy member if 0 < m(x) < 1. The set {x A |= m(x)>0} is called the support of (A, m) and the set {x A | m(x)=1} is called its kernel.

Fuzzy sets is very easy and natural to understand. If one want to define a set of gray levels one have to determine a threshold, say the gray level from 0 to 100. All gray levels from 0 to 100 are element of this set; the others do not belong to the set (See Figure 2). But the darkness is a matter. A fuzzy set can be model this property in better way. For defining this set, it needs two different thresholds 50 and 150. All the gray levels which are less than 50 are the full member of this set and all the gray levels which are greater than 150 are not the member of this set at all. The gray levels that are between 50 and 150 have a partial membership in the set.

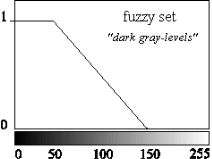
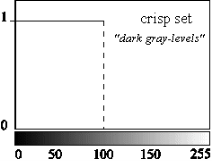
Figure 2. Representation of “dark gray-levels” with a fuzzy and crisp set.

3. Fuzzy Hyperbolization

An image I of size MxNand L gray levels can be considered as anarray of fuzzy singletons and out of which each are having a value of membership denoted its brightness relative to its brightness levels Iwith I=0 to L-1. For an image I, we can write in the notation of fuzzy sets:

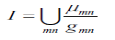
Where g, is the intensity of (m, n)th pixel and µmn its membership value. The membership function characterizes a suitable property of image (e.g. edginess, darkness, textural property) and it can be defined globally for the whole image or locally. The main principles of fuzzy image enhancement is illustrated in Figure.

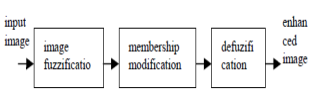
Figure 3. Fuzzy histogram hyperbolization image enhancements [2]

1. Image Fuzzification

The image fuzzification transforms the gray level of an image into values of membership function [0…1]. 2 types of transformation functions are used, the triangle membership function, and Gaussian membership functions. A triangular membership functions is shown in Figure 4 and its equation is written as,

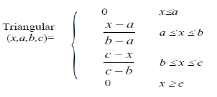
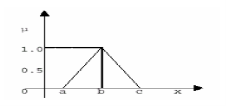
Figure 4. Triangular membership functions

The Gaussian membership function is shown in the Figure 5 and is characterized by two parameters {c, σ}. The equation for the Gaussian membership function is written as,

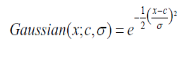
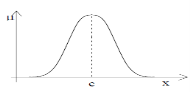
Figure 5. Gaussian membership function

2. Modification of Membership Function

This process needs to change the values of the membership functions resulted from fuzzification process. In this algorithm, the shape of the membership function is set to triangular to characterize the hedges and value of the fuzzifier β. The fuzzifier β is a linguistic hedge such that β = -0.75 + μ 1.5, so that β has a range of 0.5 – 2. The modification is carried out to the membership values by a hedges operator. The operation is called dilatation if the hedge operator β is equal to 0.5 and it is called concentration if β is equal to 2. If A is a fuzzy set and it’s represented as a set of ordered pairs of element x and its membership value is defined as μ, then Aβ is the modified version of A and is indicated by below equation

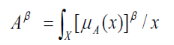
The hedge operator operates on the value of membership function as fuzzy linguistic hedges. Carrying hedge operator can be result in reducing image contrast or increasing image contrast, depending on the value of the β. The hedge operators may use to change the overall quality of the contrast of an image.

3. Image Defuzzification

After the values of fuzzy membership function has been modified, the next step is to generate the new gray level values. This process uses the fuzzy histogram hyperbolization. And this is due to the nonlinearity of human brightness perception. This algorithm modifies the membership values of gray levels by a logarithmic function:

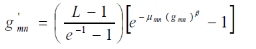
Where, μmn (gmn) is the gray level in the fuzzy membership values, β is hedge operator, and g’mn is the new gray level values.

4. Fuzzy Inference System (FIS)

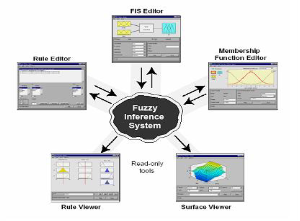
Figure 6. Fuzzy Inference Systems

Fuzzy inference is the process of mapping from the input-output using fuzzy logic. Mapping provides a basis from which it is possible to make the decisions. Process of fuzzy inference are mainly, the Membership Functions, the Logical Operations, and If-Then Rules. There are basically 2 types of fuzzy inference systems that is possible to implement in Fuzzy Logic Toolbox. 1) Mamdanitype and 2) Sugeno-type. These 2 types of inference systems vary in the way outputs are determined.

Get Help With Your Essay

If you need assistance with writing your essay, our professional essay writing service is here to help!
Find out more about our Essay Writing Service

Fuzzy inference systems has been successfully applied in fields such as data classification, decision analysis, automatic control and computer vision. As fuzzy is multidisciplinary, it can be used in fuzzy inference systems such as fuzzy-rule-based systems, fuzzy associative memory, fuzzy expert systems, fuzzy modeling, and fuzzy logic controllers, and simply fuzzy systems.

Mamdani’s fuzzy inference method is the most commonly used fuzzy method. Mamdani’s method was the first control systems designed using fuzzy set theory. It was firstly proposed in 1975 by Ebrahim Mamdani [7] to control a steam engine and boiler combination by synthesizing a set of some linguistic control rules which can be obtained from experienced human operators. Mamdani’s model was based on Lotfi Sade’s 1973 on fuzzy algorithms or complex systems and decision processes [8].

Mamdani-type inference, which defined for Fuzzy Logic Toolbox expects the output membership functions needs to be fuzzy sets. After the aggregation process, there is a fuzzy set for all the output variable that needs defuzzification. In many cases a single spike as an output membership functions are used. This type of output is usually known as a singleton output membership function. It always enhances the efficiency of the defuzzification process as it simplifies the computation required by the more simple Mamdani method, which finds the centroid of a 2D functions. Instead of integrating across the 2D function to find the centroid, one can use the weighted average of some of the data points. Sugeno-type system support this type of model. Sugeno-type systems can be used to design mathematical model of any inference system in which output membership functions are linear or constant.

5. Fuzzy rule based system

One other approach to infrared image contrast enhancement using fuzzy logic is a Takagi-Sugeno fuzzy rule based system. Takagi-Sugeno rules have consequents which are numeric functions of the input values. This approach is used to enhance the contrast of a gray-scale digital image which proposes the following rules:

IF a pixel is dark, THEN make it darker

IF a pixel is gray, THEN make it mid-gray

IF a pixel is bright, THEN make it brighter

Membership functions in a fuzzy set map all the elements of a set into some real numbers in the range [0, 1]. When the value of membership is higher, the “truth” that the set element belongs to that particular member function is higher as vice versa.

The input membership functions for an image contrast enhancement system is shown in Figure 7. The set of all input image pixel values is mapped to 3 different linguistic terms: Dark, Gray & Bright. The values μi(z) quantify the “degree of membership” of a particular input pixel intensity value to the each of the 3 member functions; denoted by the subscript (i). Thus, μdark(z) assigns value from 0 to 1 and in between to how truly “dark” an input pixel intensity value (z) is. Same way, μgray(z) and μbright(z) characterize how truly Gray or Bright a pixel value z is. The Dark and Bright input membership functions can be implemented by using a sigmoid functions and the Gray input membership function can be implemented by the Gaussian function. The sigmoid function, also known as the logistic function that is continuous and non-linear. This can be defined mathematically as follows:

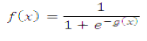
Where x is input and g(x) is gain. The Gaussian function is defined as below:

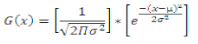
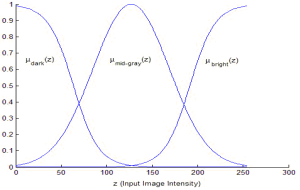
Figure 7. Input Membership Functions for the Fuzzy Rule-Based Contrast Enhancement

Three linguistic terms can be defined for the output member functions; and these are referred to as Darker, Mid-gray and Brighter. Because it is common in some of the implementations of Takagi-Sugeno systems, the output fuzzy sets are usually defined as fuzzy singleton that says the output membership functions are single-valued constants. Here the output membership function values can be selected as follows:

Darker = 0 (νd)

Mid-gray = 127 (νg)

Brighter = 255 (νb)

These are shown below:

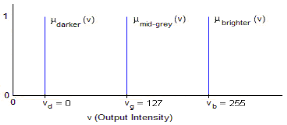
Figure 8. Output Membership Functions for the Fuzzy Rule-Based Contrast Enhancement

For a Takagi-Sugeno system design, the fuzzy logic rules which determine the outputs of system have been used the following linear combination of input and output membership function value. As the output membership functions are constants, the output νo to any input zo, is given by:

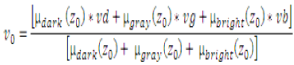
Where, μdark(z), μgray(z) and μbright(z) = the input pixel intensity values and (vd, vg and vb) = the output pixel intensity values. This relationship accomplishes the processes of implication, aggregation and defuzzification together with a numeric computation.

In case of image processing, fuzzy logic is computationally intensive, as it requires the fuzzification, processing of all rules, implication, aggregation and the defuzzification on every pixel in the input digital image. Using a Takagi-Sugeno design which uses singleton output membership functions can reduce computational complexity Figure 9 is the block diagram of the process developed for the fuzzy logic technique implemented for this work.

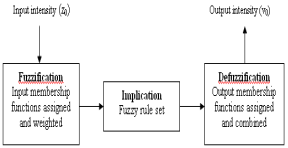
Figure 9. Flow chart for the implemented fuzzy logic process

6. Contrast enhancement using an INT-Operator from fuzzy theory

Many researchers have applied the fuzzy set theory to develop new techniques for contrast improvement. A basic fuzzy algorithm for image enhancement, using a global threshold, has been briefly recalled. Let us consider a gray level digital image, represented by the gray level values of the pixels with the range [0;1] and Let l be any gray level of a pixel in this digital image, l [0;1] .

Contrast improvement is a basic point processing operation which mainly used to maximize the dynamic range of the image. A higher contrast in an image can be achieved by darkening the gray level in the lower luminance range and brightening the ones in the upper luminance range. This processing generally implies the use of a non-linear function; Form of such a function could be the one presented in Figure 10. Mathematical expression of such a nonlinear function, Int (l) is as below:

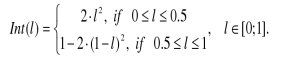
The expression represents operator in the fuzzy set theory, namely the intensification (INT) operator. When it is applied on digital images, it has the effect of contrast enhancement.

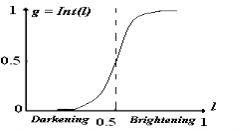
Figure 10. Fuzzy intensification

Let us denote the resulting gray levels in the contrast enhanced image by g given by:

Thus, the contrast enhanced image have gray levels of its pixels given by the nonlinear point-wise transformation in Figure 10, applied to the original gray level image.

3. Implementation on Matlab

The following are the steps which are carried out for the implementation to get the output:

1. Read the original image.

>> I = imread(‘Input image’)

2. Convert it into Gray Scale image if it is RGB image.

>> I = rgb2gray(I)

3. Add the noise to the image.

>> Z = imnoise(I,’gaussian’,0.2);

4. Calculate size of original image.

>> [row col] = size(Z);

5. Perform morphological operation on image.

To find Maximum pixel value of image

>> mx = max(max(Z));

To find Minimun pixel value of image

>> mn = min(min(d));

To find Mid point of image

>> mid = (mx+mn)/2;

6. Apply fuzzy algorithm.

7. Show the output.

>> figure,imshow(output),title (‘output enhanced image’)

4. Conclusion

Four different fuzzy approaches has been implemented to enhancement the high voltage images. Compared to the basic approaches, one can notice that fuzzy methods offer a powerful mathematical model for developing new enhancement algorithms. The global fuzzy approaches not gives satisfactory results. But here a locally adaptive procedure for fuzzy enhancement has been proposed. The contrast enhancement of high voltage images is also not satisfactory sometimes. The reason behind that is the physics of EPIDs which produces images with poor dynamics qualities and that is why sometimes there is no information in MVI to be improved. The fuzzy logic algorithms offer many different possibilities to optimize its performance, like parameters of membership functions, due to that it can certainly be expected that fuzzy image enhancement techniques can be applied in many areas of medical imaging in future.

References

[1]Farzam Farbiz, Mohammad Bager Menhaj, Seyed A. Motamedi, and Martin T. Hagan, “A new Fuzzy Logic Filter for image Enhancement” IEEE Transactions on Systems, Man, And Cybernetics-Part B: Cybernetics, Vol. 30, No. 1, February 2000.

[2]Om Parkas Verma, Madasu Hanmandlu, Anil Singh Pariah and Vamp Krishna Madasu “Fuzzy Filter for Noise Reduction in Color Images,” ICGST-GVIP Journal, Vol. 9, No. 5, September 2009, pp.29-43.

[3]Rafael C.Gonzalez and Richard, E. Woods “Digital Image Processing,” New Jersey, Pearson Prentice Hall, Third Edition – 2008.

[4]Aboul Ella Hassanien and Amr Bader, “A comparative study on digital mammography Enhancement algorithms based on Fuzzy Theory,” International Journal of Studies in Informatics and Control, SIC – Volume 12 Number 1, March 2003, pp. 21-31.

[5]Alper Pasha “Morphological image processing with fuzzy logic,” Aerospace and space technology magazines, Vol. 2, No. 3, 2006, pp.27-34.

[6]Tamalika Chaira, Ajoy Kumar Ray, “Fuzzy Image Processing and Applications with MATLAB,” CRC Press, vol. 1, 2010,pp. 47-55.

[7]Mamdani, E.H. and S. Assilian, “An experiment in linguistic synthesis with a fuzzy logic controller,” International Journal of Man-Machine Studies, Elsevier, Vol. 7, No. 1, 1975, pp. 1-13.

[8]Zadeh, L.A., “Outline of a new approach to the analysis of complex systems and decision processes,” IEEE Transactions on Systems, Man, and Cybernetics, Vol. 3, No. 1, Jan. 1973, pp. 28-44.

[9]H. R. Tizhoosh, G. Krell and B. Michaelis, “On Fuzzy Enhancement of Megavoitage Images in Radiation Therapy,” Proceedings of the 6th IEEE International Conference on Fuzzy Systems, July 1997.

[10]Stefan Schulte, Valerie De Witte, and Etienn, E.Kerre, “A Fuzzy Noise Reduction Method for Color Images,” IEEE Transactions on Image Processing, Vol. 16, Issue 5, May 2007, pp. 1425-1436.

[11]C.Castiello, G.Castellano, L.Caponetti and A.M.Fanelli, “Fuzzy Classification of Image Pixels,” IEEE International Symposium on Intelligent Signal Processing, 2003