Enigma and Lorenz Machines - Their Contribution to Computing

The purpose of this report is to understand the working of cryptography by studying the working of Enigma and Lorentz machines which were used by Germans during World War II. The report will also discuss the effect of the invention of this machines on modern day cryptography.

Cryptography has been helping humans to transmit information in secured way but the popularity of cryptography was limited to certain individuals and it was not used widely. During World War II the demand of cryptography increased which resulted in invention of Lorentz and Enigma machine by Germans. The encrypted information was important to Britain’s to gain an edge over the Germans war strategies, hence a research center was constructed in Britain’s to decode the encoded information. The report discusses the working of Enigma and Lorentz machine and the various methods adopted by Britain’s to decode the encoded information.

The report will conclude by studying the effect of the creation of the encrypting and decrypting machines on the modern-day computing.

Cryptography play an important role in human’s daily interaction with technological devices, with the advent of computing devices and internet it has become extremely important to hide private information. We often wonder how we can transfer money through internet or by using ATM cards. The sensitive personal information such as bank details are transferred securely through internet which is available to everyone. This paper tracks the events which contributed to the development of modern day cryptography and discusses the development in the field of cryptanalysis.

Cryptography is the science of secretly transferring information from one point to another so that the information is reliably transferred from one point to another, which is unintelligible to all receiver of information except the intended user. The aim of the cryptography is to prevent eavesdroppers from understanding the message. (A. Eskicioglu and L. Litwin, 2001)

The human want of secrecy of information has resulted in the invention of cryptography. Ciphers were created to hide personal information. The need to securely transmit information has increase with the advent of modern communication. Confidential information such as Business plan, financial transaction which are send over internet needs to be transferred in a secured way. Since, internet is available to everyone it important to encrypt the information which is being transferred (Zwicke, 2003).

The basic working of encryption can be divided into three parts:

1. Encryption:

Cryptography works by modifies the original information (termed plain text in cryptography) which is in readable form to encrypted form (termed ciphertext in cryptography) which is not easily interpreted by unauthorized person. The encryption process scrambles the plaintext by combining it with a key which is a random sequence of letters or numbers and produces ciphertext.

2. Transmission

Once the information is encrypted it is transferred to the intended user by various methods. For example, it could be transferred by writing it on paper or can be send via complicated modern wireless system.

3. Decryption:

After the information is received by the intended person the person tries to decode the information with a key. The key is unique and usually only the receiver has the key to decode the information (An introduction to cryptography, n.d.).

3.1 Stream cipher

Stream cipher is an encryption algorithm which encrypts one bit of data in one cycle of its operation. The stream cipher uses infinite stream of pseudorandom bits of key to encrypt the plaintext. The robustness of the stream cipher depends on the algorithm which is used to produce the key. Since, repetition in the key can cause the stream cipher to be easily predicted and the encrypted text could be easily decrypted (Villanueva, 2015).

The working of the stream cipher is explained below:

As discussed above encryption works by combining the plain text X_i with key S_i to produce ciphertext C_i . The combining process uses modulo 2 operation which is the modulus between the bits of the plaintext and ciphertext. We can denote this mathematically as C_i = X_i ⊕ S_i

To decrypt the message the same key stream is used which was used for encrypting the message.

Mathematically this can be stated as X_i = C_i ⊕ S_i  (C. Paar, J. Pelzl)

The diagram below summarizes the entire process:

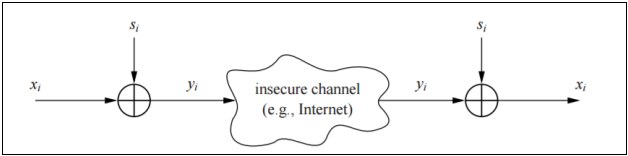
Figure 1 – Encryption and decryption with stream cipher. Reprinted from Understanding cryptography, by C. Paar, J. Pelzl, (n.d.), Retrieved from http://bit.ly/2mEit9i Copyright by Springer-Verlag Berlin Heidelberg 2010

Enigma machine eliminated the human effort of encryption by automating the process of encryption. The use of enigma machine during World War II was done to secretly transmit the classified information to remote military units.

The enigma was electro-mechanical machine which encoded the character stream to cypher text. The simplest version of the enigma machine had three motors which are interconnected with each other. It also has a plug board which is a board to interconnect letters to improve the encryption of the enigma machine. A keyboard was used to input the characters to be encoded by the machine. A light board was used to display the 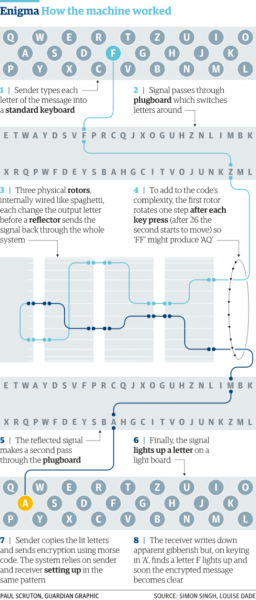encrypted letter of the plaintext character.

Figure 2 – Enigma How the machine worked. Reprinted from The guardian website, by Hern, Alex, (2014, Nov 14), Retrieved from https://www.theguardian.com/technology/2014/nov/14/how-did-enigma-machine-work-imitation-game Copyright Simon Singh.

4.1 Working

The working of enigma machine was simple. When the operator types the letter on keyboard electric signal is generated. The signal then passes through the plug board which substitutes the letter per the connection of the plug board. The signal then passes through the three rotors with internal wiring. This is where the actual encryption takes places. As mentioned above each motor consists of 26 steps of rotation before making one complete cycle. The arrangement of the three motors was such that when the first motor completes a full rotation the second motor would move by one step. The same step is applicable for third motor.

After passing through the connection of motors the signal is then reflected and again passes thorough the plug board. After passing through the plug board the signal lights up the appropriate letter on the light board providing the encrypted letter of the plain text character.

The Lorentz machine was developed by C. Lorentz in Berlin. In 1940s Germans saw the need to establish secured communication between German high command in Wünsdorf close to berlin and German army throughout Europe. With the invention of mechanical machine and electronic boards it became possible to build a machine capable of encrypting the message which was send to remote army. The Lorenz machine was used for sending tactical information (Smart, n.d.).

Lorentz machine uses Lorentz cipher which was based on Baudot code. Let’s discuss about the working of Baudot code.

Baudot Code:

It used five bit of data to encode characters. Baudot code was a standard means of communication via teleprinter. Since five bits were insufficient to represent all the characters on the keyboard. Hence the code was divided into two states called “letter shifts” and “figures shifts”. To toggle between the two states a control character was used, there were other characters which had special functions such as “space”.

To understand the working of Baudot code let’s take an example of encrypting the word “Hello”. The first step is to fill the Paper tape with holes and insert the paper tape into telegraph to send the message. To punch holes in the paper tape the position of the holes needs to be determined which was obtained from the Baudot code table. These holes were converted to bits and then transferred by teleprinter.

Figure 3 – The Baudot printing telegraphy system. Second Edition. Reprinted from Circuitousroot website, by Pendry, H, W. (1919) Retrieved from http://www.circuitousroot.com/artifice/telegraphy/tty/codes/

5.1 Lorenz Cipher

The Baudot code is taken as input by the Lorenz cipher. The Lorenz cipher consisted of 12 motors which are separated into 3 pairs. Each motor had different number of pins on it as shown in figure below:

Figure 4 – An Enigma machine rotor. Reprinted from Plus magazine website, by Ellis Claire. (2005, Mar 1). Picture retrieved from https://plus.maths.org/content/exploring-enigma Copyright by Simon Singh

Each pin could store either 0 or 1 based on the configuration of the machine. The configuration of the machine (setting the starting position of each motor) was performed by the operator of the machine and the same configuration of the machine was used at the receiving end to decrypt the message.

The Lorentz machine was divided into three pairs of motors as shown below:

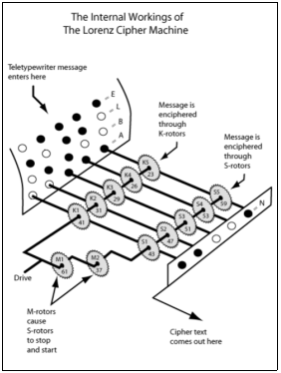
Figure 5 – The internal working of the Lorentz cipher machine. Reprinted from the Rochester institute website, by Payne, Japnce. (n.d.), Retrieved from https://people.rit.edu/japnce/payne/images/rotorsall.png

The three pair of motors are termed as K, M, and S. The description of each pair of motors is discussed below:

K motors: These consist of 5 motors with following pin configuration K1=41, K2=31, K3=29, K4=26, K5=23. This set of motors shift by one pin for every character which was encoded.

M motors: These consist of 2 motors with following pin configuration M1=61, M2=37.

This set of motors shift by one pin for every character which was encoded. Further the output of the M motors decided whether the S motors should be rotated by one pin or should remain unchanged.

S motors: These consist of 5 motors with following pin configuration S1=43, S2=47, S3=51, S4=53, S5=59. This set of motors shift by one pin based on the output of M motors.

Working

The 5 bits of the characters are first X-OR with the 5 bits of K motor. The output is then again X-OR with the 5 bits of S motors to get the cypher text. At the receiving end since the Lorentz cipher is a symmetric cipher, the same configuration is used to set up the Lorentz machine at receiving end and the encrypted message is decrypted.

The mathematical formula of the encryption and decryption process is as follows:

Suppose Message = M, Cipher text = C, Cypher = E

M ⊕ E = C (Encryption)

C ⊕ E = M (Decryption) (Smart, n.d.)

Most of the technology that was in existence during World War II was like that which was used in World War I. The telegraph, which was type-printed using a typewriter was widely used commercially and by military personnel. In the late 1800’s an Italian scientist, Guglielmo Marconi discovered the radio communication. However, it wasn’t until the early 1900’s that this technology was adopted for military purposes. It was the year 1914 and most major military powers of the world has started relying extensively on this technology but there was a problem – there were no security mechanisms in place for a wireless signal to hide the messages being transmitted. The U.S. soon used a more sophisticated version of this technology as soon as Frequency Modulation was invented in 1920.

Figure 6 – Soldier during World War II using telegraphic switchboard

Another important element of communication technology invented before and during the World War II was the RADAR technology. Developed by the U.S. navy for military use, these were signals sent in the microwave wavelength. It was an entirely new way of surveillance that enabled the allies to see in total darkness and find out about enemy ships in the distant sea or air.  Radar used small-short signals that were sent into a direction using an antenna. This would return the position and speed of an object which would serve as a critical early warning tool.

Radar navigation implementation by the German bombers meant that the previous tactics of indiscriminate, area-based bombing was now replaced by more accurate precision targeting. Then there were the German fire control radars, Lichtenstein SN2 was mounted on top of airplanes and had an effective range of 2.5 miles.

A methodology that had been in existence for a quite a while but was found of prime use during the World War II was Cryptography. Cryptography emerged as the saving grace to answer all questions about the immense need of secrecy. Cryptography had been in existence for over a thousand years but it wasn’t until the early 19^th century that mathematicians came together to build a machine that would be used for a very specific purpose – send messages during times of war. During this period, Cypher machines were developed under extreme secrecy. These machines were of the mechanical and electromechanical kind. Out of the two, the later were developed by Germans into what they called the Enigma machine

Allies and enemies developed and adopted the use of cryptographic communications of all sorts during this period. While Germans were focusing on techniques to build machines for encryption, the UK was busy trying to perform cryptanalysis on these machines. Numerous machines came out of Germany that used cryptography in its own unique way. FISH, as the UK’s Bletchley Park codenamed them, were a series of German stream ciphers developed during the World War II era. The enigma in the early 1920s which was of the electro-mechanical sort that used a keyboard, rotors and a spindle to do the tricks. Another machine known as the Lorenz cipher was simultaneously developed as a form was a rotor stream cipher and started its use in military since 1941 in a ‘SZ’ form. The “tunny” cipher as it was called was used for wireless telegraphy which eventually and unfortunately for the Germans, quite soon led to the interception of its messages.

Poland came up with its own cryptographic machine called Bomba, which meant cryptographic bomb in Polish. While there is less information available about why it was named so, Bomba was a glorified Enigma machine in more ways than one. It was developed after the mathematician and its creator, Marian Rejewski studied by breaking apart an Enigma. Put simply, it was a multiple Enigma machine that used an electrical power aggregate of six Enigmas. Most countries like Poland, United States and the UK devoted their time and resources in cryptanalysis of these machines.

Bletchley Park in England was extremely instrumental in bringing about a new era with the cryptanalysis or code breaking of messages that were being transmitted by the Germans during the World War II. The Lorenz machine was a stream cipher that encoded/streamed electrical pulses over a telephone line. The technique used was something we call ‘XOR’ today which is an addition operation. A key property of XOR is that if one was to run the Ciphertext through the same key again, the original message could be found. The exploitation of this very concept of the Lorenz cipher led to its success cryptanalysis.

One day after a 4000-letter message was sent out to Vienna, the sender who encodes the message received a response from the receiver asking to resend the message since they had not received the message. The sender reset the Lorenz machine and started to abbreviate a few words to make the process quicker. At this time, Bletchley Park had two copies of the same message and the prime mistake was that both were sent using the same key. The folks at Bletchley park were not just great mathematicians, but they also had an exceptional sense of awareness. They proceeded to add the two messages together, essentially cancelling out the keys. They were now left with two messages added together and then John Tiltman, an experience code breaker who not just able to figure out the message, but also figured out the key.

John Tiltman gave this key to Bill Tutte, a young graduate from Cambridge who liked solving puzzles. He was able to out the length of the key by writing it down in rows with the aim to find out patterns. Bill Tutte found that the pattern of the wheel on the right had a period of 41. However, the pattern was not perfect and had an element of randomness which suggested that a wheel on the left was used that moved only sometimes. This information was enough for other mathematicians to jump onboard and fully figure out the Lorenz machine.

The Enigma on the other hand had multiple variations in the structure of the machine throughout its useful life to be cracked at one go. The earlier versions of the Enigma were using a 3-rotor structure which was used as the main subject by the Polish Cipher Bureau. Marian Rejewski who worked for the bureau made significant developments in breaking the Enigma, without having much access to any of the official information about its inner workings.

Rejewski developed a bomba machine in the process, this cryptanalysis machine was build using the observations Rejewski gathered that showed that the first three letters of a message were the same as the second three. Rejewski’s method failed when in 1938 the Germans increased the rotors to include two additional ones. It was Alan Turing who developed a sophisticated Bombe that used statistics and the Bayes law for calculating the probability to narrow down on the number of possibilities. The bombe machines were also quickly updated to test the hypothesis.

Figure 7 – The British Bombe currently in display at the Bletchley Park

Alan Turing’s Bombe was composed of drums which together simulated an enigma and each drum replicated the functioning of one rotor of the machine. The objective of the Turing’s bombe was to find out the key used by the Enigma, the starting position of the rotors and the “steckers” or plugs. The drums were designed to move from a set starting position every time. The movement was designed with the help of statistics and the Bayes law, hence the “key space” was greatly reduced thereby reducing the run time.

Alan Turing has been regarded as one of the biggest contributors to defeating the German navy by helping the Allied Forced during the World War II. It is believed that the British employed 200 Bombes during the Second World War and collectively these Bombes decoded 4000 messages on any given day. The cryptanalysis of the Enigma is believed to have contributed to saving millions of lives and is identified as a prime reason why the war ended years before what it could’ve lasted.

Britain’s World War II codebreakers were centrally located at Bletchley Park, a code-breaking center run by the United Kingdom Government Code and Cypher School (GC&CS). They primarily focused on deciphering German Enigma and Lorenz communications and producing “Ultra” intelligence (Hinsley, 1996). Ultra was the designation for high level encrypted Axis-power intelligence the codebreakers intercepted and decrypted (Hinsley, 1993). Ultra-intelligence generated by decrypted Enigma and Lorenz signals is credited with shortening the war, and without it the outcome of the war may have been different (Hinsley, 1996).

The Enigma machine was the German’s primary encryption method during the war. Alan Turing, working at Bletchley Park in 1939, created the Bombe, which was an electromechanical machine used to decrypt Enigma ciphers (Smith, 2007). Gordon Welchman refined the Bombe in 1940 with a diagonal board, increasing the Bombe’s efficiency (Budiansky, 2000). Welchman’s diagonal board addressed the plug board vulnerability in the Enigma. The Bombe was based on the Bomba, a Polish machine designed to break Enigma ciphers, which was created by Marian Rejewski (Kozaczuk, 1984). The creation of the functional Bombes led to Allies’ deciphering of Enigma signals.

Beginning in 1940, Germany started developing more advanced machines that used the Lorenz cipher. The first was called the SZ40 machine, which was codenamed “Tunny” by the British codebreakers at Bletchley Park, and was followed by subsequent versions (SZ40A, SZ40B, and SZ42 (Copeland, 2006). These machines produced more complex ciphers than the Enigma, and were ultimately defeated by the “1+2 break in” method created by Bill Tutte (Copeland, 2006).

Multiple advanced decryption machines were designed to combat the Lorenz ciphers. First was the British Tunny Machine, which replicated the functions of the SZ40 machines. With the proper cam settings, it was able to produce clear text from cipher text that was input into it (Hinsley, 1993). Built on the Tunny machines, the Heath Robinson, or “Robinsons”, were created to automate the “1+2 break in” (Copeland, 2006). They ran paper tapes to find the wheel settings of the Lorenz machine. Although they were functional, issues with keeping the paper tapes synchronized and slow processing speed limited their effectiveness (Copeland, 2006).

Working on the Robinsons at Bletchley Park, Tommy Flowers was instrumental in the advancement of the Colossus computer. Colossus was capable of faster processing than the Robinsons due to processing electronically. This also allowed for only one paper tape, which did not have to be synchronized with another and could be run at a faster speed, around 5,000 characters per second (Copeland, 2006).

Although the Colossus computer was created first, the American ENIAC was often credited for being the first electronic digital computer ever made. This was caused by Colossus being shrouded in secrecy after World War II. The term “computer” originally referred to a human operator who performed mathematical computations. As the need for more demanding and complex computations increased, a push for electronic or digital computing began (Copeland, 2006).

Computers like Colossus and ENIAC were called “program-controlled” computers, in which programs each computer was to process were not stored in the computer’s memory – they had to be manually programmed. For Colossus and ENIAC, this involved modifying wiring by hand using plugs and switches. Modern computers utilize a “stored-program” concept, in which the programs a computer runs are stored in that computer’s memory (Copeland, 2006).

The concept of the modern computer started with Alan Turing in 1936. He described a “universal computing machine”, containing limitless memory that stored both data and programs. A scanner would process the data based on the selected program. The use of any program with the data allowed the computer to process any calculation a human could, making it universal. Being universal allowed the computer to switch from one task to another, as opposed to a completely different and unique machine needing to be created for each individual task (Copeland, 2006).

Turing’s concept can be seen in modern computing today, where personal computers and mobile devices (smartphones, etcetera) store both data and programs, and can easily switch between different tasks based on the user’s needs. Programming to achieve a particular task is relatively simple in comparison – installing a program in a modern computer is much less complex compared to rewiring something like the Colossus computer or creating a completely new machine entirely.

As discussed, the Germans and Axis powers used Enigma and Lorenz ciphers heavily for their encrypted communications in World War II. The decryption of Enigma and Lorenz was key for the Allies and the development of “Ultra” intelligence, which likely shortened the war by years.

In the end, the need for decrypting Enigma and Lorenz was the initial catalyst the eventually led to modern computing. Colossus, being the first electronic computer, spearheaded the push into the modern stored-program concept that computers and modern devices use today. Without this need for computing power, the world may well have progressed in a much different way.

References

Budiansky, S. (2000). Battle of Wits: The Complete Story of Codebreaking in World War II. Free Press: 1734.

Cooper, S., & Leeuwen, J. (2013). Alan Turing: His Work and Impact. Saint Louis, U.S.: Elsevier Science.

Copeland, B., ed. (2006). Colossus: The Secrets of Bletchley Park’s Codebreaking Computers. Oxford: Oxford University Press.

Enigma Machine. (2006). In J. Merriman & J. Winter (Eds.), Europe Since 1914: Encyclopedia of the Age of War and Reconstruction (Vol. 2, pp. 964-966). Detroit: Charles Scribner’s Sons. Retrieved from http://go.galegroup.com/ps/i.do?p=GVRL&sw=w&u=csuf_main&v=2.1&it=r&id=GALE%7CCX3447000319&sid=exlibris&asid=50a327ace003888aadf98172a87c0eb6

Eskicioglu, A., & Litwin, L. (2001). Cryptography. IEEE Potentials, vol. 20, no. 1, pp. 36-38. doi: 10.1109/45.913211

Hinsley, F. H. (1993). The Influence of ULTRA in the Second World War. Retrieved from https://web.archive.org/web/20120706194507/http://www.cl.cam.ac.uk/research/security/Historical/hinsley.html

Hinsley, F. H. & Stripp, A. (1993). Codebreakers: The Inside Story of Bletchley Park. Oxford: Oxford University Press.

Kidwell, P. (2007). Technology and Culture. 48(3), pp. 663-664. Retrieved March 9, 2017, from JSTOR database.

Kozaczuk, W. (1984). Enigma: How the German Machine Cipher Was Broken, and How It Was Read by the Allies in World War Two. Frederick, MD: University Publications of America.

Paar, C., Pelzl, J. (2010). Understanding Cryptography. Dordrecht, London, New York: Springer-Verlag.

Smart, N. (n.d.). Cryptography: An Introduction. Retrieved from http://www.cryptocellar.org/files/NP_Smart_Cryptography.pdf

Smith, M. (2007) [1998]. Station X: The Codebreakers of Bletchley Park. London: Pan McMillan Ltd.

The Ohio State University Fisher College of Business. (n.d.). An Introduction to Cryptography. Retrieved from https://fisher.osu.edu/~muhanna.1/pdf/crypto.pdf

Villanueva, J. (2015). An Introduction to Stream Ciphers and Block Ciphers. Retrieved from http://www.jscape.com/blog/stream-cipher-vs-block-cipher

Welchman, G. (2005). The Hut Six Story: Breaking the Enigma Codes. Cleobury Mortimer, England: M&M Baldwin.

Zwicke, A. (2003). An Introduction to Modern Cryptosystems. SANS Institute. Retrieved from https://www.giac.org/paper/gsec/2604/introduction-modern-cryptosystems/104482