Compressive Sensing: Performance Comparison of Measurement
| ✅ Paper Type: Free Essay | ✅ Subject: Engineering |
| ✅ Wordcount: 2991 words | ✅ Published: 31 Aug 2017 |
Compressive Sensing: A Performance Comparison of Measurement Matrices
Y. Arjoune, N. Kaabouch, H. El Ghazi, and A. Tamtaoui
Abstract–Compressive sensing paradigm involves three main processes: sparse representation, measurement, and sparse recovery process. This theory deals with sparse signals using the fact that most of the real world signals are sparse. Thus, it uses a measurement matrix to sample only the components that best represent the sparse signal. The choice of the measurement matrix affects the success of the sparse recovery process. Hence, the design of an accurate measurement matrix is an important process in compressive sensing. Over the last decades, several measurement matrices have been proposed. Therefore, a detailed review of these measurement matrices and a comparison of their performances is needed. This paper gives an overview on compressive sensing and highlights the process of measurement. Then, proposes a three-level measurement matrix classification and compares the performance of eight measurement matrices after presenting the mathematical model of each matrix. Several experiments are performed to compare these measurement matrices using four evaluation metrics which are sparse recovery error, processing time, covariance, and phase transition diagram. Results show that Circulant, Toeplitz, and Partial Hadamard measurement matrices allow fast reconstruction of sparse signals with small recovery errors.
Index Terms– Compressive sensing, sparse representation, measurement matrix, random matrix, deterministic matrix, sparse recovery.
TRADITIONAL data acquisition techniques acquire N samples of a given signal 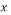 sampled at a rate at least twice the Nyquist rate in order to guarantee perfect signal reconstruction. After data acquisition, data compression is needed to reduce the high number of samples because most of the signals are sparse and need few samples to be represented. This process is time consuming because of the large number of samples acquired. In addition, devices are often not able to store the amount of data generated. Therefore, compressing sensing is necessary to reduce the processing time and the number of samples to be stored. This sensing technique includes data acquisition and data compression in one process. It exploits the sparsity of the signal to recover the original sparse signal from a small set of measurements [1]. A signal is sparse if only a few components of this signal are nonzero. Compressive sensing has proven itself as a promising solution for high-density signals and has major applications ranging from image processing [2] to wireless sensor networks [3-4], spectrum sensing in cognitive radio [5-8], and channel estimation [9-10].
sampled at a rate at least twice the Nyquist rate in order to guarantee perfect signal reconstruction. After data acquisition, data compression is needed to reduce the high number of samples because most of the signals are sparse and need few samples to be represented. This process is time consuming because of the large number of samples acquired. In addition, devices are often not able to store the amount of data generated. Therefore, compressing sensing is necessary to reduce the processing time and the number of samples to be stored. This sensing technique includes data acquisition and data compression in one process. It exploits the sparsity of the signal to recover the original sparse signal from a small set of measurements [1]. A signal is sparse if only a few components of this signal are nonzero. Compressive sensing has proven itself as a promising solution for high-density signals and has major applications ranging from image processing [2] to wireless sensor networks [3-4], spectrum sensing in cognitive radio [5-8], and channel estimation [9-10].
As shown in Fig. 1. compressive sensing involves three main processes: sparse representation, measurement, and sparse recovery process. If signals are not sparse, sparse representation projects the signal on a suitable basis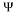 so the signal can be sparse. Examples of sparse representation techniques are Fast Fourier Transform (FFT), Discrete Wavelet Transform (DWT), and Discrete Cosine Transform (DCT) [11]. The measurement process consists of selecting a few measurements,
so the signal can be sparse. Examples of sparse representation techniques are Fast Fourier Transform (FFT), Discrete Wavelet Transform (DWT), and Discrete Cosine Transform (DCT) [11]. The measurement process consists of selecting a few measurements, 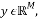 from the sparse signal
from the sparse signal 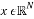 that best represents the signal where
that best represents the signal where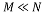 . Mathematically, this process consists of multiplying the sparse signal
. Mathematically, this process consists of multiplying the sparse signal 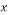 by a measurement matrix
by a measurement matrix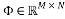 . This matrix has to have a small mutual coherence or satisfy the Restricted Isometry Property. The sparse recovery process aims at recovering the sparse signal
. This matrix has to have a small mutual coherence or satisfy the Restricted Isometry Property. The sparse recovery process aims at recovering the sparse signal 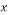 from the few measurements
from the few measurements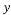 selected in the measurement process given the measurement matrix Φ. Thus, the sparse recovery problem is an undetermined system of linear equations, which has an infinite number of solutions. However, sparsity of the signal and the small mutual coherence of the measurement matrix ensure a unique solution to this problem, which can be formulated as a linear optimization problem. Several algorithms have been proposed to solve this sparse recovery problem. These algorithms can be classified into three main categories: Convex and Relaxation category [12-14], Greedy category [15-20], and Bayesian category [21-23]. Techniques under the Convex and Relaxation category solve the sparse recovery problem through optimization algorithms such as Gradient Descent and Basis Pursuit. These techniques are complex and have a high recovery time. As an alternative solution to reduce the processing time and speed up the recovery, Greedy techniques have been proposed which build the solution iteratively. Examples of these techniques include Orthogonal Matching Pursuit (OMP) and its derivatives. These Greedy techniques are faster but sometimes inefficient. Bayesian based techniques which use a prior knowledge of the sparse signal to recover the original sparse signal can be a good approach to solve sparse recovery problem. Examples of these techniques include Bayesian via Laplace Prior (BSC-LP), Bayesian via Relevance Vector Machine (BSC-RVM), and Bayesian via Belief Propagation (BSC-BP). In general, the existence and the uniqueness of the solution are guaranteed as soon as the measurement matrix used to sample the sparse signal satisfies some criteria. The two well-known criteria are the Mutual Coherence Property (MIP) and the Restricted Isometry Property (RIP) [24]. Therefore, the design of measurement matrices is an important process in compressive sensing. It involves two fundamental steps: 1) selection of a measurement matrix and 2) determination of the number of measurements necessary to sample the sparse signal without losing the information stored in it.
selected in the measurement process given the measurement matrix Φ. Thus, the sparse recovery problem is an undetermined system of linear equations, which has an infinite number of solutions. However, sparsity of the signal and the small mutual coherence of the measurement matrix ensure a unique solution to this problem, which can be formulated as a linear optimization problem. Several algorithms have been proposed to solve this sparse recovery problem. These algorithms can be classified into three main categories: Convex and Relaxation category [12-14], Greedy category [15-20], and Bayesian category [21-23]. Techniques under the Convex and Relaxation category solve the sparse recovery problem through optimization algorithms such as Gradient Descent and Basis Pursuit. These techniques are complex and have a high recovery time. As an alternative solution to reduce the processing time and speed up the recovery, Greedy techniques have been proposed which build the solution iteratively. Examples of these techniques include Orthogonal Matching Pursuit (OMP) and its derivatives. These Greedy techniques are faster but sometimes inefficient. Bayesian based techniques which use a prior knowledge of the sparse signal to recover the original sparse signal can be a good approach to solve sparse recovery problem. Examples of these techniques include Bayesian via Laplace Prior (BSC-LP), Bayesian via Relevance Vector Machine (BSC-RVM), and Bayesian via Belief Propagation (BSC-BP). In general, the existence and the uniqueness of the solution are guaranteed as soon as the measurement matrix used to sample the sparse signal satisfies some criteria. The two well-known criteria are the Mutual Coherence Property (MIP) and the Restricted Isometry Property (RIP) [24]. Therefore, the design of measurement matrices is an important process in compressive sensing. It involves two fundamental steps: 1) selection of a measurement matrix and 2) determination of the number of measurements necessary to sample the sparse signal without losing the information stored in it.
A number of measurement matrices have been proposed. These matrices can be classified into two main categories: random and deterministic. Random matrices are generated by identical or independent distributions such as Gaussian, Bernoulli, and random Fourier ensembles. These matrices are of two types: unstructured and structured. Unstructured type matrices are generated randomly following a given distribution. Example of these matrices include Gaussian, Bernoulli, and Uniform. These matrices are easy to construct and satisfy the RIP with high probability [26]; however, because of the randomness, they present some drawbacks such as high computation and costly hardware implementation [27]. Structured type matrices are generated following a given structure. Examples of matrices of this type include the random partial Fourier and the random partial Hadamard. On the other hand, deterministic matrices are constructed deterministically to have a small mutual coherence or satisfy the RIP. Matrices of this category are of two types: semi-deterministic and full-deterministic. Semi-deterministic type matrices have a deterministic construction that involves the randomness in the process of construction. Example of semi-deterministic type matrices are Toeplitz and Circulant matrices [31]. Full-deterministic type matrices have a pure deterministic construction. Examples of this type measurement matrices include second-order Reed-Muller codes [28], Chirp sensing matrices [29], binary Bose-Chaudhuri-Hocquenghem (BCH) codes [30], and quasi-cyclic low-density parity-check code (QC-LDPC) matrix [32]. Several papers that provide a performance comparison of deterministic and random matrices have been published. For instance, Monajemi et al. [43] describe some semi-deterministic matrices such as Toeplitz and Circulant and show that their phase transition diagrams are similar as those of the random Gaussian matrices. In [11], the authors provide a survey on the applications of compressive sensing, highlight the drawbacks of unstructured random measurement matrices, and they present the advantages of some full-deterministic measurement matrices. In [27], the authors provide a survey on full-deterministic matrices (Chirp, second order Reed-Muller matrices, and Binary BCH matrices) and their comparison with unstructured random matrices (Gaussian, Bernoulli, Uniform matrices). All these papers provide comparisons between two types of matrices of the same category or from two types of two different categories. However, to the best of knowledge, no previous work compared the performances of measurement matrices from the two categories and all types: random unstructured, random structured, semi-deterministic, and full-deterministic. Thus, this paper addresses this gap of knowledge by providing an in depth overview of the measurement process and comparing the performances of eight measurement matrices, two from each type.
The rest of this paper is organized as follows. In Section 2, we give the mathematical model behind compressive sensing. In Section 3, we provide a three-level classification of measurement matrices. Section 4 gives the mathematical model of each of the eight measurement matrices. Section 5 describes the experiment setup, defines the evaluation metrics used for the performance comparison, and discusses the experimental results. In section 6, conclusions and perspectives are given.
Compressive sensing exploits the sparsity and compresses a k-sparse signal 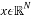 by multiplying it by a measurement matrix
by multiplying it by a measurement matrix 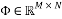 where
where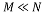 . The resulting vector
. The resulting vector 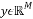 is called the measurement vector. If the signal
is called the measurement vector. If the signal 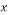 is not sparse, a simple projection of this signal on a suitable basis
is not sparse, a simple projection of this signal on a suitable basis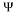 , can make it sparse i.e.
, can make it sparse i.e. 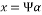 where
where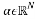 . The sparse recovery process aims at recovering the sparse signal
. The sparse recovery process aims at recovering the sparse signal 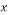 given the measurement matrix
given the measurement matrix 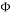 and the vector of measurements
and the vector of measurements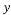 . Thus, the sparse recovery problem, which is an undetermined system of linear equations, can be stated as:
. Thus, the sparse recovery problem, which is an undetermined system of linear equations, can be stated as:
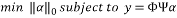 (1)
(1)
Where 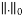 is the
is the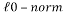 ,
, 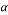 is a sparse signal in the basis
is a sparse signal in the basis 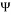 ,
, 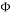 is the measurement matrix, and
is the measurement matrix, and 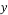 is the set of measurements.
is the set of measurements.
For the next of this paper, we consider that the signals are sparse i.e. 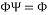 and
and 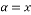 . The problem (1) then can be written as:
. The problem (1) then can be written as:
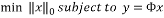 (2)
(2)
This problem is an NP-hard problem; it cannot be solved in practice. Instead, its convex relaxation is considered by replacing the 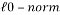 by the
by the 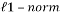 . Thus, this sparse recovery problem can be stated as:
. Thus, this sparse recovery problem can be stated as:
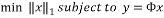 (3)
(3)
Where 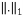 is the
is the 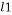 -norm,
-norm, 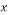 is the k-parse signal,
is the k-parse signal, 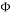 the measurement matrix and
the measurement matrix and 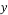 is the set of measurements.
is the set of measurements.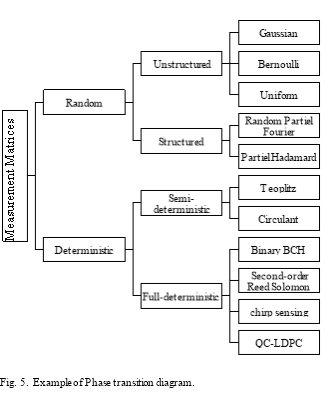 Having the solution of problem (3) is guaranteed as soon as the measurement matrix
Having the solution of problem (3) is guaranteed as soon as the measurement matrix  has a small mutual coherence or satisfies RIP of order
has a small mutual coherence or satisfies RIP of order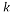 .
.
Definition 1: The coherence measures the maximum correlation between any two columns of the measurement matrix 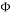 . If
. If 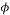 is a
is a 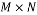 matrix with normalized column vector
matrix with normalized column vector 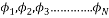 , each
, each 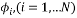 is of unit length. Then the mutual coherence Constant (MIC) is defined as:
is of unit length. Then the mutual coherence Constant (MIC) is defined as:
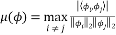 (4)
(4)
Compressive sensing is concerned with matrices that have low coherence, which means that a few samples are required for a perfect recovery of the sparse signal.
Definition 2: A measurement matrix satisfies the Restricted Isometry Property if there exist a constant 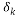 such as:
such as:
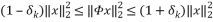 (5)
(5)
Where 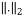 is the
is the 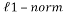 and
and 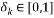 is called the Restricted Isometry Constant (RIC) of
is called the Restricted Isometry Constant (RIC) of 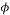 which should be much smaller than 1.
which should be much smaller than 1.
As shown in the Fig .2, measurement matrices can be classified into two main categories: random and deterministic. Matrices of the first category are generated at random, easy to construct, and satisfy the RIP with a high probability. Random matrices are of two types: unstructured and structured. Matrices of the unstructured random type are generated at random following a given distribution. For example, Gaussian, Bernoulli, and Uniform are unstructured random type matrices that are generated following Gaussian, Bernoulli, and Uniform distribution, respectively. Matrices of the second type, structured random, their entries are generated following a given function or specific structure. Then the randomness comes into play by selecting random rows from the generated matrix. Examples of structured random matrices are the Random Partial Fourier and the Random Partial Hadamard matrices. Matrices of the second category, deterministic, are highly desirable because they are constructed deterministically to satisfy the RIP or to have a small mutual coherence. Deterministic matrices are also of two types: semi-deterministic and full-deterministic. The generation of semi-deterministic type matrices are done in two steps: the first step consists of the generation of the entries of the first column randomly and the second step generates the entries of the rest of the columns of this matrix based on the first column by applying a simple transformation on it such as shifting the element of the first columns. Examples of these matrices include Circulant and Toeplitz matrices [24]. Full-deterministic matrices have a pure deterministic construction. Binary BCH, second-order Reed-Solomon, Chirp sensing, and quasi-cyclic low-density parity-check code (QC-LDPC) matrices are examples of full-deterministic type matrices.
Based on the classification provided in the previous section, eight measurement matrices were implemented: two from each category with two from each type. The following matrices were implemented: Gaussian and Bernoulli measurement matrices from the structured random type, random partial Fourier and Hadamard measurement matrices from the unstructured random type, Toeplitz and Circulant measurement matrices from the semi-deterministic type, and finally Chirp and Binary BCH measurement matrices from the full-deterministic type. In the following, the mathematical model of each of these eight measurement matrices is described.
A. Random Measurement Matrices
Random matrices are generated by identical or independent distributions such as normal, Bernoulli, and random Fourier ensembles. These random matrices are of two types: unstructured and structured measurement random matrices.
1) Unstructured random type matrices
Unstructured random type measurement matrices are generated randomly following a given distribution. The generated matrix is of size 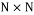 . Then M rows is randomly selected from N. Examples of this type of matrices include Gaussian, Bernoulli, and Uniform. In this work, we selected the Random Gaussian and Random Bernoulli matrix for the implementation. The mathematical model of each of these two measurement matrices is given below.
. Then M rows is randomly selected from N. Examples of this type of matrices include Gaussian, Bernoulli, and Uniform. In this work, we selected the Random Gaussian and Random Bernoulli matrix for the implementation. The mathematical model of each of these two measurement matrices is given below.
a) Random Gaussian matrix
The entries of a Gaussian matrix are independent and follow a normal distribution with expectation 0 and variance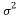 . The probability density function of a normal distribution is:
. The probability density function of a normal distribution is:
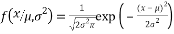 (6)
(6)
Where 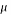 is the mean or the expectation of the distribution,
is the mean or the expectation of the distribution, 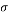 is the standard deviation, and
is the standard deviation, and 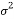 is the variance.
is the variance.
This random Gaussian matrix satisfies the RIP with probability at least 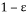 given that the sparsity satisfy the following formula:
given that the sparsity satisfy the following formula:
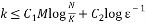 (7)
(7)
Where 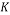 is the sparsity of the signal,
is the sparsity of the signal, 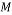 is the number of measurements, and
is the number of measurements, and 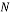 is the length of the sparse signal [36].
is the length of the sparse signal [36].
b) Random Bernoulli matrix
A random Bernoulli matrix 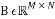 is a matrix whose entries take the value
is a matrix whose entries take the value 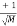 or
or 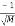 with equal probabilities. It, therefore, follows a Bernoulli distribution which has two possible outcomes labeled by n=0 and n=1. The outcome n=1 occurs with the probability p=1/2 and n=0 occurs with the probability q=1-p=1/2. Thus, the probability density function is:
with equal probabilities. It, therefore, follows a Bernoulli distribution which has two possible outcomes labeled by n=0 and n=1. The outcome n=1 occurs with the probability p=1/2 and n=0 occurs with the probability q=1-p=1/2. Thus, the probability density function is:
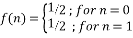 (8)
(8)
The Random Bernoulli matrix satisfies the RIP with the same probability as the Random Gaussian matrix [36].
2) Structured Random Type matrices
The Gaussian or other unstructured matrices have the disadvantage of being slow; thus, large-scale problems are not practicable with Gaussian or Bernoulli matrices. Even the implementation in term of hardware of an unstructured matrix is more difficult and requires significant space memory space. On the other hand, random structured matrices are generated following a given structure, which reduce the randomness, memory storage, and processing time. Two structured matrices are selected to be implemented in this work: Random Partial Fourier and Partial Hadamard matrix. The mathematical model of each of these two measurement matrices is described below:
a) Random Partial Fourier matrix
The Discrete Fourier matrix 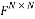 is a matrix whose
is a matrix whose 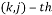 entry is given by the equation:
entry is given by the equation:
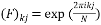 (9)
(9)
Where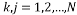 .
.
Random Partial Fourier matrix which consists of choosing random M rows of the Discrete Fourier matrix satisfies the RIP with a probability of at least 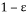 , if:
, if:
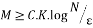 (10)
(10)
Where M is the number of measurements, K is the sparsity, and N is the length of the sparse signal [36].
b) Random Partial Hadamard matrix
The Hadamard measurement matrix is a matrix whose entries are 1 and -1. The columns of this matrix are orthogonal. Given a matrix H of order n, H is said to be a Hadamard matrix if the transpose of the matrix H is closely related to its inverse. This can be expressed by:
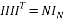 (11)
(11)
Where 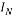 is the
is the 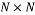 identity matrix,
identity matrix, 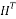 is the transpose of the matrix
is the transpose of the matrix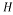 .
.
The Random Partial Hadamard matrix consists of taking random rows from the Hadamard matrix. This measurement matrix satisfies the RIP with probability at least 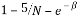 provided
provided 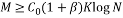 with
with 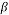 and
and 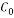 as positive constants, K is the sparsity of the signal, N is its length and M is the number of measurements [35].
as positive constants, K is the sparsity of the signal, N is its length and M is the number of measurements [35].
B. Deterministic measurement matrices
Deterministic measurement matrices are matrices that are designed following a deterministic construction to satisfy the RIP or to have a low mutual coherence. Several deterministic measurement matrices have been proposed to solve the problems of the random matrices. These matrices are of two types as mentioned in the previous section: semi-deterministic and full-deterministic. In the following, we investigate and present matrices from both types in terms of coherence and RIP.
1) Semi-deterministic type matrices
To generate a semi-deterministic type measurement matrix, two steps are required. The first step is randomly generating the first columns and the second step is generating the full matrix by applying a simple transformation on the first column such as a rotation to generate each row of the matrix. Examples of matrices of this type are the Circulant and Toeplitz matrices. In the following, the mathematical models of these two measurement matrices are given.
a) Circulant matrix
For a given vector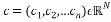 , its associated circulant matrix
, its associated circulant matrix 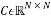 whose
whose 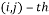 entry is given by:
entry is given by:
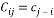 (11)
(11)
Where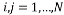 .
.
Thus, Circulant matrix has the following form:
C=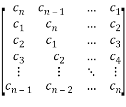
If we choose a random subset 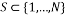 of cardinality
of cardinality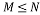 , then the partial circulant submatrix
, then the partial circulant submatrix 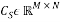 that consists of the rows indexed by
that consists of the rows indexed by 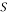 achieves the RIP with high probability given that:
achieves the RIP with high probability given that:
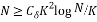 (12)
(12)
Where 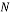 is the length of the sparse signal and
is the length of the sparse signal and 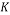 its sparsity [34].
its sparsity [34].
b) Toeplitz matrix
The Toeplitz matrix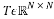 , which is associated to a vector
, which is associated to a vector 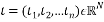 whose
whose 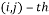 entry is given by:
entry is given by:
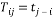 (13)
(13)
Where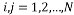 . The Toeplitz matrix is a Circulant matrix with a constant diagonal i.e.
. The Toeplitz matrix is a Circulant matrix with a constant diagonal i.e. 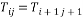 . Thus, the Toeplitz matrix has the following form:
. Thus, the Toeplitz matrix has the following form:
T=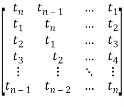
If we randomly select a subset  of cardinality
of cardinality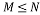 , the Restricted Isometry Constant of the Toeplitz matrix restricted to the rows indexed by the set S satisfies
, the Restricted Isometry Constant of the Toeplitz matrix restricted to the rows indexed by the set S satisfies 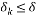 with a high probability provided
with a high probability provided
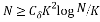 (14)
(14)
Where 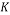 is the sparsity of the signal and
is the sparsity of the signal and 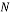 is its length [34].
is its length [34].
2) Full-deterministic type matrices
Full-deterministic type matrices are matrices that have pure deterministic constructions based on the mutual coherence or on the RIP property. In the following, two examples of deterministic construction of measurements matrices are given which are the Chirp and Binary Bose-Chaudhuri-Hocquenghem (BCH) codes matrices.
a) Chirp Sensing Matrices
The Chirp Sensing matrices are matrices their columns are given by the chirp signal. A discrete chirp signal of length ð‘š has the form:
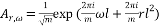
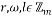 (15)
(15)
The full chirp measurement matrix can be written as:
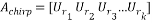 (16)
(16)
Where 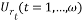 is an
is an 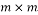 matrix with columns are given by the chirp signals with a fixed
matrix with columns are given by the chirp signals with a fixed 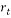 and base frequency
and base frequency 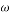 values that vary from 0 to m-1. To illustrate this process, let us assume that
values that vary from 0 to m-1. To illustrate this process, let us assume that 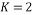 and
and 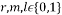
Given 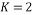 , The full chirp matrix is as follows:
, The full chirp matrix is as follows:

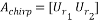
In order to calculate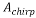 , the matrices
, the matrices 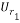 and
and 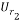 should be calculated. Using the chirp signal, the entries of these matrices are calculated and given as:
should be calculated. Using the chirp signal, the entries of these matrices are calculated and given as:
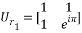 ;
;
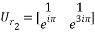
Thus, we get the  chirp measurement matrix
chirp measurement matrix 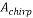 as:
as:
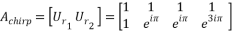
Given that 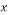 is a
is a 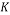 -sparse signal with chirp code measurements
-sparse signal with chirp code measurements 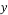 and
and 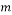 is the length of the chirp code. If
is the length of the chirp code. If
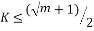 (17)
(17)
then 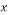 is the unique solution to the sparse recovery algorithms. The complexity of the computation of the chirp measurement matrix is
is the unique solution to the sparse recovery algorithms. The complexity of the computation of the chirp measurement matrix is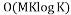 . The main limitation of this matrix is the restriction of the number of measurements to
. The main limitation of this matrix is the restriction of the number of measurements to 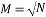 [29].
[29].
b) Binary BCH matrices
Let denote 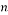 as a divisor of
as a divisor of 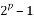 for some integer
for some integer 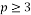 an
an
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


