Arc-Surface Intersection Method
| ✅ Paper Type: Free Essay | ✅ Subject: Engineering |
| ✅ Wordcount: 2774 words | ✅ Published: 30 Aug 2017 |
Arc-Surface Intersection Method to Calculate Cutter-Workpiece Engagements for Generic Cutter in Five-Axis Milling
Zhou-Long Li, Xin-Zhi Wang, Li-Min Zhu[*]
State Key Laboratory of Mechanical System and Vibration, School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, P.R. China
Abstract: Calculating cutter-workpiece engagements (CWEs) is essential to the physical simulation of milling process that starts with the prediction of cutting forces. As for five-axis milling of free form surfaces, the calculation of CWEs remains a challenge due to the complicated and varying engagement geometries that occur between the cutter and the in-process workpiece. In this paper, a new arc-surface intersection method (ASIM) is proposed to obtain CWEs for generic cutter in five-axis milling. The cutter rotary surface is first represented by the family of circles which are generated by slicing the cutter with planes perpendicular to the tool axis. Based on the envelope condition, two grazing points on each circle are analytically derived, which divide the circle into two arcs. The feasible contact arc (FCA) is then extracted to intersect with workpiece surfaces. Using arc/surface intersection and distance fields based approach, the boundary of the closed CWEs is accurately and efficiently calculated. Compared with the solid modeler based method and the discrete method, the ASIM has higher computational efficiency and accuracy. Moreover, an analytical solution for calculating CWEs can be obtained with this method in five-axis milling of the workpiece merely comprising of flat and quadric surfaces. Finally, two case tests are implemented to confirm the validity of the ASIM and comparisons have been made with a Vericut based system which utilizes the Z-buffer method. The results indicate that the ASIM is computationally efficient, accurate and robust.
Keywords: Cutter-workpiece engagements; Grazing points;Feasible contact arc; Swept volume; Generic cutter;Five-axis machining
1. Introduction
Five-axis milling has been widely used in the production of complex parts found in aerospace, automotive, die-mold and biomedical industries [1-5]. The machining process is usually costly and time-consuming especially for high accuracy required parts. Hence, the main focus of five-axis machining is to reduce cycle times while ensuring manufacturing precision. Generally, optimal cutting parameters are selected by the industry through simulating the physics of the cutting process, i.e. cutting force and chatter stability. As for the machining process simulation and optimization, it is required to model the cutter-workpiece engagements (CWEs) which are the portions of the cutter participating in machining at a given instant of time.
Due to the complex geometry of the workpiece and the varying tool motions, the accurate and efficient way to calculate CWEs of five-axis milling has been very limited. Some researchers tried to extract the CWEs in analytical ways. Gupta et al. [6] presented an analytical method to determine the CWE functions with the half-spaces in the following cases: circular cut and linear half-space. Budak et al. [7] proposed the bounding point coordinate method to calculate the depth of cut, lead, and tilt angles, which determine the CWE boundaries in five-axis milling. Kiswanto et al. [8] calculated the CWEs during the semi-finish milling process by finding the lower engagement point and the upper engagement point. However, these methods are only applicable for milling of flat workpiece surfaces. Since the workpiece in five-axis milling usually consists of complex shapes, the usage of the analytical approaches is limited.
For the calculation of CWEs in five-axis milling, the most common approaches can be classified into two major categories: discrete modeling methods and solid modeling methods. Discrete modeling approaches can further be categorized into two groups: vector based methods and polygon based methods. Vector modeling divides the workpiece into finite units with regular interval methods well known as Z-map [9], Z-buffer [10, 11], Dexel [12] and Octree [13]. The commonly used Z-map method represents the workpiece as a series of evenly distributed parallel vectors. The length of these vectors is reduced while the cutter moves through the workpiece which is similar to cutting blades of grass [14]. Based on this method, several studies have been conducted to verify the correctness of tool paths and support the physical simulation for both three-axis and five-axis milling. Baek et al. [15, 16] used the Z-map method to perform tool path verification through calculating the intersection points between vectors and the tool swept surface in three-axis milling. Zhu et al. [17], Fussell et al. [10] and Zhang [18] model the CWE geometry to predict cutting force for five-axis sculptured surface milling using vector based method. Polygon based methods have also received some attention [19-21]. Aras et al. [20] presented a methodology that maps a polyhedral representation of the removal volume from a Euclidean space into a parametric space to find CWEs for three-axis milling. Yao et al. [21] developed a hybrid approach that utilizes an exact model of a cutter to intersect with a tessellated model of a workpiece. Though computationally efficient and mathematically tractable, these techniques suffer from the contradiction between the dispersed precision of workpiece decomposition and the computational efficiency. In other words, the high accuracy computation of CWEs requires the high discrete resolution of the workpiece which comes with the expense of large store memory and computational requirements.
Solid modeling offers a high level of accuracy for NC simulation. It is now widely used in CAD and CAM areas with the developing computer technology. The commonly used solid modeling representation schemes are constructive solid geometry (CSG) and boundary representation (B-Rep). Spence et al. [22, 23] identified CWEs using a CSG based process simulation system to predict cutting force. Recently, Lazoglu et al. [24] proposed a novel B-Rep based method to determine the complex CWEs in supporting five-axis milling of free-form surfaces. Aras et al. [25] obtained the closed boundaries of the CWEs by performing surface/surface intersections between in-process workpiece and feasible contact surfaces (FCS). Although solid modeling methods have been recognized as the most accurate approach to extract CWE geometry, it is far from being widely used in practical application due to its low computational efficiency and poor robustness. For instance, the computational complexity of the CSG approach is 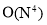 , where
, where 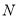 denotes the number of tool movements [26]. What’s worse, as the data structure size grows quickly during simulation, topological errors due to numerical inaccuracy will be stacked [27]. To overcome such problems, Ferry et al. [28] proposed a semi-discrete solid modeling technique called parallel slicing method (PSM) for five-axis flank milling where the removal volume is sliced into a number of parallel planes along a common axis. Yang et al. [27] developed a solid trimming method which reduces the abundant surface/surface intersection operations compared with the traditional Boolean operations. However, the improvements of these approaches in computational efficiency and robustness are limited.
denotes the number of tool movements [26]. What’s worse, as the data structure size grows quickly during simulation, topological errors due to numerical inaccuracy will be stacked [27]. To overcome such problems, Ferry et al. [28] proposed a semi-discrete solid modeling technique called parallel slicing method (PSM) for five-axis flank milling where the removal volume is sliced into a number of parallel planes along a common axis. Yang et al. [27] developed a solid trimming method which reduces the abundant surface/surface intersection operations compared with the traditional Boolean operations. However, the improvements of these approaches in computational efficiency and robustness are limited.
In this paper, we present a new arc-surface intersection method (ASIM) to extract CWEs in five-axis milling. First, the cutter rotary surface is sliced into a family of circles by a set of planes perpendicular to the tool axis. Then, based on the envelope condition, the grazing points of the family of circles are analytically computed. By connecting the two grazing points on each circle, a feasible contact arc (FCA) which locates at the front along the feed direction is obtained. Engagement arcs are extracted accurately and efficiently by intersecting the FCA with workpiece surfaces and determining whether the endpoint of the FCA is inside the workpiece volume based on distance fields. Finally, entry/exit angles of CWEs at each axis height are obtained to plot the CWE map which can be directly used for cutting force prediction. As the boundary of CWEs at each axis height is accurately determined by the arc/surface intersection rather than the abundant Boolean operation, this method well solves the problems of poor computational efficiency and robustness in solid modeling methods and low computational accuracy in discrete methods. Comparisons between our methodology and those commonly used in the literatures are presented in Table 1.
Table 1 Comparison of the CWE calculation methods
|
Approach |
Workpiece representation |
CWE calculation |
Efficiency |
Accuracy |
Robustness |
|
Solid modeling methods |
CSG or B-Rep |
Surface/surface |
Low |
Exact |
Poor |
|
Vector based methods |
Vectors |
Line/surface |
High |
Approximate |
Strong |
|
Polygon based methods |
Polygons |
Plane/plane |
High |
Approximate |
Strong |
|
This method |
B-Rep |
Arc/surface |
Middle |
Exact for each disc |
Strong |
The remainder of this paper is organized as follows: generation of the feasible contact arcs is described in Section 2, followed by the five-axis CWE extraction methodology in Section 3. Implementations are given in Section 4, and conclusion is summarized in Section 5.
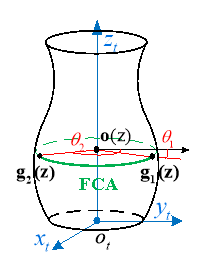
2 Generation of the Feasible Contact Arcs
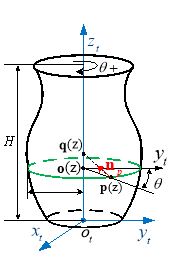
CWEs are the instantaneous contact regions between the tool surface and the in-process workpiece. To support the commonly used force prediction model [17, 22, 29], where the cutter is divided into a set of axial disc elements, CWEs at each cutter location (CL) are defined by mapping the engagement region on the cutter surface onto a parametric space defined by the engagement angle versus the depth of cut. In this paper, the cutter rotary surface is first discretized into a family of circles which are generated by slicing the cutter with planes perpendicular to the tool axis, as shown in Fig. 1. Then, these circles are used as primitives to describe the general cutter.
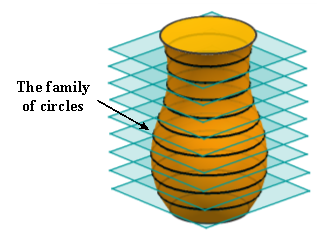
Fig. 1 Axial discretization of the general cutter surface
In five-axis milling, the grazing curve is the set of points on the cutter surface that remain on the envelope surface. As shown in Fig. 2, it divides the cutter’s surface into two parts. The one in orange facing the cutting direction is defined as the front-facing part, which can be actually involved in machining. The other one in light grey is defined as the back-facing part, which is impossible to engage with the in-process workpiece.
As for the primitive circle on the cutter surface, it is spilt into two partial arcs by the grazing points. The solid one shown in Fig. 2 is named as the feasible contact arc (FCA) since it locates at the tool front-facing part. Given that the CWEs are the subsets of the tool front-facing part rather than the back-facing part, determination of the FCA helps us to obtain CWEs in a more efficient way.
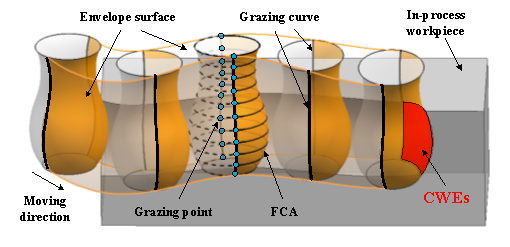
Fig. 2 Illustration of the FCA and CWEs in five-axis milling
As illustrated in Fig. 3, the tool motion is usually represented by two guiding curves 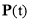 and
and 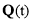 [30]. To describe the instantaneous cutter position and orientation during NC machining, the moving tool coordinate frame
[30]. To describe the instantaneous cutter position and orientation during NC machining, the moving tool coordinate frame 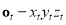 is set up at
is set up at 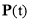 . Its axises are determined as follows
. Its axises are determined as follows
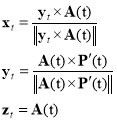 , (1)
, (1)
where 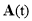 represents the tool axis orientation at time t with
represents the tool axis orientation at time t with 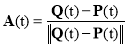 .
.
|
(a) |
(b) |
Fig. 3 The enveloping characteristic of the rotary cutter undergoing general spatial motion
When the cutter moves with respect to time t, the point on the cutter surface can be expressed as
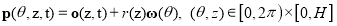 , (2)
, (2)
with 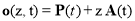 ,
,
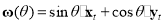 .
.
According to ref. [31], we have the expression of the intersection point between the normal vector of point 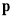 and tool axis
and tool axis
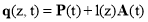 , (3)
, (3)
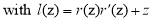 .
.
Then, the unit normal vector at the point 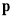 is
is
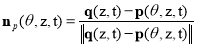 .(4)
.(4)
The moving speed of the point 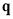 on the tool axis is determined by the equation
on the tool axis is determined by the equation
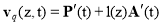 .(5)
.(5)
According to the envelope condition for the surface of revolution proposed by Gong et al. [31], the grazing point should meet the following equation
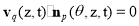 . (6)
. (6)
By substituting Eq. (4) and (5) into Eq. (6), we have
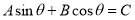 , (7)
, (7)
with 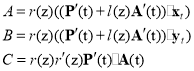 .
.
Eq. (7) can be written in the following form
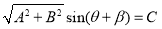 , (8)
, (8)
If 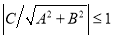 ,
, 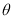 can be resolved from Eq. (8) as follows:
can be resolved from Eq. (8) as follows:
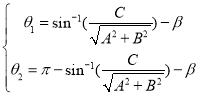 . (9)
. (9)
Substituting 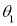 ,
, 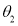 and a given height z back into Eq. (2), we can get closed-form solutions of two grazing points on the corresponding primitive circle.
and a given height z back into Eq. (2), we can get closed-form solutions of two grazing points on the corresponding primitive circle.
Based on the fact that the FCA locates at the front along the moving direction, each point 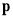 on the FCA should satisfy the following condition:
on the FCA should satisfy the following condition:
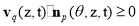 . (10)
. (10)
According to Eq. (2) and Eq. (9), the FCA of the cutter at axis height 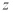 , as shown in Fig. 4, can be expressed as
, as shown in Fig. 4, can be expressed as
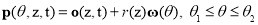 . (11)
. (11)
Hence, according to Eq. (11), the family of FCAs at any CL can be generated, which is then used as the primitive to extract CWEs.
Fig. 4 Illustration of the feasible contact arc
3 Arc-Surface Intersection Method to Calculate Cutter-Workpiece Engagements
The conventional methods to extract CWEs in five-axis milling usually need to update the workpiece at every CL, which is quite computational memory and time consuming. As the FCA is used as the primitive to extract engagement arcs, there is no need to update workpiece during the material removal process unless the cutter moves to the next tool path. As shown in Fig. 5, the entry/exit angles can be determined according to the circumferential angles of endpoints of the engagement arc in red, and there may be more than one pair of entry/exit angles at each axis height. Hence, in this section, a vector 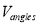 is built to store the entry/exit angles of engagement arcs, which is then used to create the CWE map.
is built to store the entry/exit angles of engagement arcs, which is then used to create the CWE map.
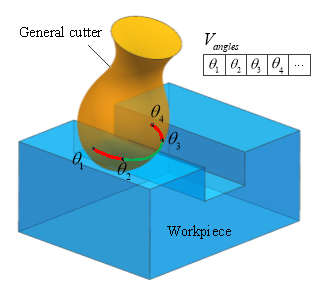
Fig. 5 Illustration of storing engagement angles in a vector 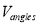
3.1 Intersection of FCA with Workpiece Surfaces
To extract CWEs, we first intersect the FCA with workpiece surfaces to obtain the part of boundary points of engagement arcs. As the workpiece is usually comprised of polygons, quadric surfaces and polynomial surfaces, this paper focuses on the intersection problem of arcs with these three types of surface. It is worth noting that the intersection of the arc with polygon or quadric surface can be analytically computed.
3.2.1 Intersection of Arc with Polygon
Polygon is represented by a list of n vertices: 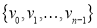 . The plane of the polygon is defined by the following algebraic equation:
. The plane of the polygon is defined by the following algebraic equation:
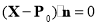 , (12)
, (12)
where 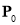 is a point on the plane which can be determined by selecting an arbitrary vertex, and
is a point on the plane which can be determined by selecting an arbitrary vertex, and 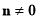 is a normal vector of the plane which is computed using the cross product of the vectors formed by that vertex and its neighbors.
is a normal vector of the plane which is computed using the cross product of the vectors formed by that vertex and its neighbors.
Substituting Eq. (11) into Eq. (12) yields
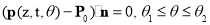 . (13)
. (13)
Similar to the solving method of Eq. (6), we can analytically obtain at most two intersection points. An even-odd rule algorithm is adopted to determine whether the intersection point is within the boundaries of the polygon [32]. If any intersection point lies inside the polygon, add the corresponding circumferential angle 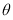 into
into 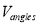 .
.
3.2.2 Intersection of Arc with Quadric Surface
The general implicit form for a quadric surface can be compactly represented as
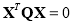 , (14)
, (14)
with 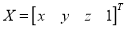 ,
, 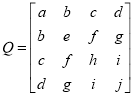 .
.
The intersection of the arc with a quadric can be computed by substituting the homogeneous form of Eq. (11) into Eq. (14):
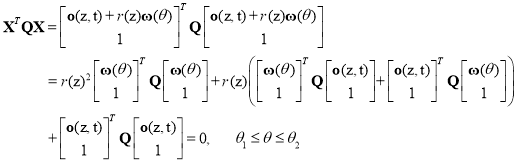 . (15)
. (15)
The above equation can be simplified into the following form:
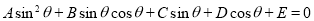 . (16)
. (16)
Set 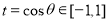 , Eq. (16) can be transformed to a quartic equation of the form
, Eq. (16) can be transformed to a quartic equation of the form
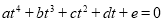 . (17)
. (17)
The above equation can be solved analytically by means of a method discovered by Lodovico Ferrari (http://mathworld.wolfram.com/QuarticEquation.html). There are at most four solutions of 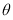 , which are then added into
, which are then added into  .
.
3.2.3 Intersection of Arc with Polynomial Surface
Polynomial surface is commonly used in computer graphics, as it offers great flexibility and precision for handling both analytic and modeled shapes. Its common types include Bézier surfaces, B-spline surfaces and non-uniform rational B-spline (NUBRS) surfaces. The NURBS technique is the only expression standard in STEP (ISO, 1991) for free-form curves and surfaces and gives the uniform mathematical expression for all graphics [33]. Hence, in this section, NURBS surface is taken into account.
A NURBS surface of degree p in the u direction and degree q in the v direction is a bivariate vector-valued piecewise rational function of the form
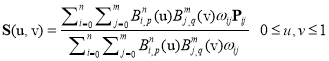 , (18)
, (18)
where 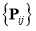 denote a bidirectional control set,
denote a bidirectional control set, 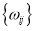 are the weights,
are the weights, 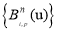 and
and 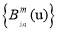 are the non-rational B-spline basis functions.
are the non-rational B-spline basis functions.
Then, the intersection of the arc with a NURBS surface can be computed by simultaneously solving Eq. (11) and Eq. (18) using Newton iteration [32]. To improve the computational efficiency, a hierarchy of axis-aligned bounding boxes (AABB) is used which allows for quick rejection and thus can help avoid many expensive intersection computations [34]. If any intersection point is obtained, add the corresponding circumferential angle 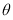 into
into 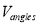 .
.
3.2 Determination of Whether the Endpoint of FCA is Inside the Workpiece Volume Based on Distance Fields
Since it is not enough for the extraction of engagement arcs merely to use the circumferential angles of the intersection points, it is necessary to determine the inclusion relation between the endpoint of the FCA and the workpiece volume. As for the arbitrary endpoint 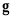 , a signed Euclidean distance field [35]
, a signed Euclidean distance field [35] 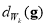 , which defines the minimum distance from
, which defines the minimum distance from 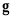 to the boundary of workpiece
to the boundary of workpiece 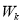 , is calculated to determine whether
, is calculated to determine whether 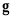 lies inside
lies inside 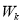 . It can be represented as follows
. It can be represented as follows
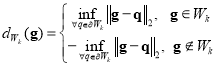 , (19)
, (19)
where 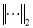 is the Euclidean norm,
is the Euclidean norm, 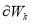 denotes the boundary of
denotes the boundary of 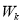 . To improve the computational efficiency, an octree bounding volume hierarchy is used to obtain spatial localization of geometric operations [36]. If the endpoint
. To improve the computational efficiency, an octree bounding volume hierarchy is used to obtain spatial localization of geometric operations [36]. If the endpoint 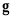 lies inside the workpiece
lies inside the workpiece 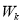 , add the corresponding circumferential angle
, add the corresponding circumferential angle 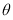 into
into 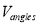 .
.
3.3 Creation of the CWE Map
There may be multiple engagement arcs corresponding to each primitive circle on the cutter surface, as shown in Fig. 6, where the red arcs denote the engagement arcs. Each engagement arc has its corresponding entry/exit angle. From Fig. 6, it can be found that the entry/exit angles occur in pairs in ascending order. Since 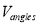 obtained above is an unordered list, we first sort it from small to large. Then each pair of entry/exit angle can be obtained by taking each element out of
obtained above is an unordered list, we first sort it from small to large. Then each pair of entry/exit angle can be obtained by taking each element out of
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal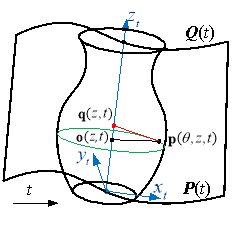
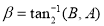 .
.