Adequacy of Strong Improvement to Explain RAP

CASE STUDY OF APPROACH TO CONSIDER UNCERTAIN COMPONENTS’ FAILURE RATES IN SERIES-PARALLEL RELIABILITY SYSTEMS WITH REDUNDANCY ALLOCATION

Abstract

The principle reason for this review is to demonstrate the adequacy of strong improvement to explain RAP. The erlang distribution is used to implement robust optimization. The dynamic values attained by the failure rate is found to be a correct one. Another computation technique is introduced to consider dynamic qualities for failure rate in RAP. Also, because of complex redundancy Allocation Problem, two Simulated Annealing (SA) and Ant Colony Optimization (ACO) calculations are intended to decide the strong framework regarding indeterminate qualities for parameters. Another presumption is that every subsystem can have dynamic excess systems. Keeping in mind the end goal to take care of this issue and demonstrate effectiveness of proposed calculations, an issue in writing is unraveled and talked about.

1. INTRODUCTION of Articles

The planning for a system to select the components simultaneously is called the Redundancy Allocation Problem. Here these components are joined by several types to maximize the system reliability including all the properties in the system which are obtained. The reliability range should be maximum for different products to design the best system for a problem. The series parallel system can be of three types such as reliability allocation, redundancy allocation, and reliability redundancy allocation. For the first type the reliability limit is reduced for the usage of the resources in component’s reliability. The other type contains the redundancy limit to increase the reliability of the system to maximize the system level constraints. The failure rate of every components is studied on the journal articles which were in a determinable surrounding. The failure rate is very difficult to determine to be a exact one in practical environment for various factors as it may vary. The failure rates under various factors are affected. The failure rates aren’t any specified values in this article. The robust optimization is used to solve the reliability allocation problem for failure rates. In this article, the robustness with the redundancy allocation problem is explained and the mathematical model is developed. There are two algorithms used to find the indeterminate qualities for the parameters. The Simulated Annealing and Ant Colony Optimization algorithm is used and tested by the problem.

Nomenclature

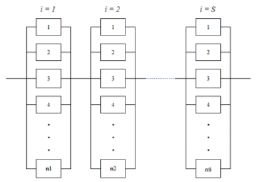
i : index of subsystems where i 1,2,…,si .

ni: number of components used in subsystem i .

ni:set of components used in all subsystems expect subsystem

r_i,zi (t) : reliability of component i z for subsystem i at time t

_i,zi, K_i,zi : scale and shape parameters for the Gamma distribution of component i z in subsystem i

_i,zi(n_i, ni-) : function of robust failure rate for component i z in subsystem i .

C,W : system level constraint limits for cost and weight, respectively.

R(t; z,n) : system reliability at time t for designing vectors z and n .

2. Explanation of the work presented in journal articles

ROBUSTNESS DEFINITION IN RELIABILITY ALLOCATION PROBLEM

To maximize the total reliability of a robust system the following assumptions are considered

1. Components failure rate are changed as a result of change in system structure
2. The constraints of the problem are predetermined for any changes in system structure.
3. The total components in the subsystem is increasing when we consider the failure rate of this component
4. The increase in the reliability of the component is caused by the decreased failure rate.

THE ROBUST MODEL IN RELIABILITY ALOCATION PRROBLEM

It is conceivable to execute two unique systems for parts of subsystems in Reliability allocation problem. The first is dynamic methodology in which every single repetitive part will begin to work at the same time from time zero. Interestingly, there are three unique variations of the cool, warm and hot methodologies rather for the second technique which is known as standby technique. In warm variation and in contrast with cool one, it would be more conceivable that segments flop before beginning to work on system. In the event that we utilize hot variation, it would not be essential that segments are working or they are sit and their failure rates will be consistent any way. As indicated by these definitions, we can create same numerical model for two unique techniques of hot standby and dynamic repetition. The repetitive parts are consecutively utilized as a part of the system at segment failure times and each repetitive segment in the standby system can be worked just when it is exchanged on. At the point when the segment in operation falls flat, one of the excess units is changed on to proceed with the system operation. The 1, 2 and 3 equations are as follows

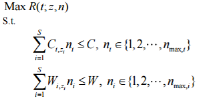
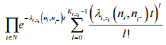– 4

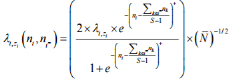– 5

As per these derivations, a model is introduced in which failure rates will be computed in light of condition (5). This condition helps us to consider new failure rate values instead of steady ones. In addition, these new proposed qualities are more down to earth for genuine issues and will help fashioners to reduce existent crevices amongst hypothesis and practice. Then again, we cover the existent deficiencies which have never been focused on in the writing by building up another technique to compute failure rates. The robust relations are solved by the two algorithms Simulated and Ant Colony Optimizing for the redundancy allocation problem.

3. Discussion of Contributions

SIMULATED ANNEALING ALGORITHM FOR RAP

Simulated Annealing is a standout amongst the most well-known probabilistic meta-heuristics to locate an adequate answer for advancement issues which was essential proposed by Kirkpatrick, Gelatt and Vecchi. This calculation depends on the relationship between the way toward tempering of solids and the arrangement philosophy of combinatorial advancement issues. One the most essential invaluable of the SA is keeping from rapidly focalizing to nearby ideal arrangement. This normal for SA is multiplied by tolerating better arrangements as well as the more regrettable neighbor arrangements with a specific likelihood to escape from a nearby ideal. It is observable that the likelihood of tolerating a more regrettable arrangement relies on upon the estimation of temperature; thus, while the temperature diminishes, the likelihood of tolerating a more terrible arrangement diminishes too.

ANT COLONY OPTIMIZING ALGOROTHM FOR RAP

Truly, ACO was firstly presented by Dorigo, Maniezzo and Colorni [3]. Key thought of subterranean insect frameworks depends on conduct of characteristic ants that prevail to discover most limited way from their home to nourishment sources by imparting by means of an aggregate memory that comprises of pheromone trails. Ants have a tendency to take after a way with a high pheromone level when numerous ants move in a typical range and they move arbitrarily when no pheromone is accessible. Then again, ants don’t pick their bearings in light of level of pheromone only, but instead consider nearness of home and sustenance source, individually.

4. Discussion of Dificiency and Potential Improvements

The improvements to be made on this article are to solve large sized problems the heuristic algorithms were not developed and the flexible model to consider the dynamic values can be improved. An another development to be made is to show a robust model for selecting different types of parts simultaneously. The graphical theory could be used to develop by a new model

5. Summary

In this review, a nonlinear numerical model is produced for powerful arrangement parallel system with excess portion issue where, it has never been focused on strong enhancement approaches for this issue. In this model, we show another technique to compute part failure rates which is more versatile to genuine issues. Additionally, we create two reproduced tempering and insect province streamlining calculations which brought about proper arrangements, speedily. The last outcomes demonstrate that ACO calculation can bring about happier arrangements in contrast with SA calculation.

There are three major advantages of robust model, The first is that utilizing this model will help us to create adaptable arrangements which are more functional to cover deficiencies amongst hypothesis and practice. The second one is that this model produces arrangements with higher framework dependability as opposed to those ones which have been displayed in writing. At last, the third one is that the created arrangements will be powerful and by changing the conditions, they can even now be proper arrangements which are near ideal arrangements.

References

[1]Ali Ghafarian Salehi Nezhada,*, Abdolhamid Eshraghniaye Jahromib, Mohammad Hassan Salmanic, Fereshte Ghasemid, an approach to consider uncertain components’ failure rates in series-parallel reliability systems with redundancy allocation.International Journal of Industrial Engineering (2016)

[2] S. Kirkpatrick, C.D.J. Gelatt, M.P. Vecchi, Optimization by simulated annealing, Science. 220 (1983), pp.671-680

[3]M. Dorigo, V. Maniezzo, A. Colorni, Positive feedback as a search strategy, Technical Report. (1991).

[4]D.W. Coit, A.E. Smith, Optimization Approaches to the Redundancy Allocation Problem for Series-Parallel Systems,

Cited as Proceedings of the Fourth Industrial Engineering Research Conference. (1995).