Dual Trapezoidal Fuzzy Number and Its Applications
| ✅ Paper Type: Free Essay | ✅ Subject: Computer Science |
| ✅ Wordcount: 1700 words | ✅ Published: 12 Mar 2018 |
Abstract
In this paper, we introduce Convergence of α-Cut. We define at which point the α-Cut converges to the fuzzy numbers it will be illustrated by example using dual trapezoidal fuzzy number and Some elementary applications on mensuration are numerically illustrated with approximated values.
KeyWords: Fuzzy number, α-Cut, Dual trapezoidal fuzzy number, Defuzzification.
Introduction
Fuzzy sets have been introduced by Lotfi. A. Zadeh (1965). Fuzzy numbers were first introduce by Zadeh in 1975.There after theory of fuzzy number was further studied and developed by Dubois and Prade, R.Yager Mizomoto, J.Buckly and Many others. Since then many workers studied the theory of fuzzy numbers and achieved fruitful results. The fuzziness can be represented by different ways one of the most useful representation is membership function. Also depending the nature and shape of the membership function the fuzzy number can be classified in different forms, such as triangular fuzzy number, trapezoidal fuzzy number etc. A fuzzy number is a quantity whose values are imprecise, rather than exact as is the case with single valued number. Fuzzy numbers are used in statistics computer programming, engineering and experimental science. So far fuzzy numbers like triangular fuzzy number, trapezoidal fuzzy numbers, pentagonal, hexagonal, octagonal pyramid and diamond fuzzy numbers have been introduced with its membership functions. These numbers have got many applications like non-linear equations, risk analysis and reliability. In this paper, we introduce Dual trapezoidal fuzzy numbers with its membership functions and its applications. Section one presents the introduction, section two presents the basic definition of fuzzy numbers section three presents Dual trapezoidal fuzzy numbers and its applications and in the final section we give conclusion.
Basic Definitions
Fuzzy set
A fuzzy set A in a universe of discourse X is defined as the following set of pairs A= {(x, µA(x)): x X} Here µA(x) : x
X} Here µA(x) : x is a mapping called the degree of membership function of the fuzzy set A and µA(x) is called the membership value of x
is a mapping called the degree of membership function of the fuzzy set A and µA(x) is called the membership value of x X in the fuzzy set These membership grades are often represented by real numbers ranging from [0, 1].
X in the fuzzy set These membership grades are often represented by real numbers ranging from [0, 1].
Fuzzy Number
A fuzzy set A defined on the universal set of real number R is said to be a fuzzy number if its membership function has satisfy the following characteristics.
( i) μA (x) is a piecewise continuous
(ii) A is convex, i.e., µA (αx1 + (1-α) x2) ≥ min (µA(x1), µA(x2)) É x1 ,x2 R É α
R É α [0,1]
[0,1]
(iii) A is normal, i.e., there exist xo  R such that µA (xo)=1
R such that µA (xo)=1
Trapezoidal Fuzzy Number
A trapezoidal fuzzy number represented with four points as A = (a b c d), Where all a, b, c, d are real numbers and its membership function is given below where a≤ b≤ c≤ d
µA(x)=
DUAL TRAPEZOIDAL FUZZY NUMBER
Dual Trapezoidal Fuzzy Number
A Dual Trapezoidal fuzzy number of a fuzzy set A is defined as ADT= {a, b, c, d (α)} Where all a, b, c, d are real numbers and its membership function is given below where a≤b≤c≤d
µDT(x) =
where α is the base of the trapezoidal and also for the inverted reflection of the above trapezoidal namely a b c d
 Figure: Graphical Representation of Dual Trapezoidal fuzzy Number
Figure: Graphical Representation of Dual Trapezoidal fuzzy Number
DEFUZZIFICATION
Let ADT= (a, b, c, d, ð›‚) be a dual trapezoidal fuzzy number .The defuzzification value of ADT is an approximate real number. There are many method for defuzzification such as Centroid Method, Mean of Interval Method , Removal Area Method etc. In this Paper We have used Centroid area method for defuzzification .
CENTROID OF AREA METHOED
Centroid of area method or centry of gravity method. It obtains the centre of area (X*)
occupied by the fuzzy sets.It can be expressed as
X* = 
Defuzzification Value for dual trapezoidal fuzzy number
Let ADT= {a, b, c, d (α)} be a DTrFN with its membership function
µDT(x) =
Using centroid area method
 +
+ dx+
dx+ +
+ +
+ dx
dx
=  +
+  +
+  +
+
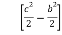 +
+  +
+
=
= 
 =
=  +
+ +
+  dx+
dx+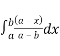 +
+ +
+ dx
dx
=
= 
= c + d – a – b
Defuzzification = 
= 
= 
APPLICATION
In this section. We have discussed the convergence of ð›‚-cut using the example of dual trapezoidal fuzzy number.
CONVERGENCE OF α-CUT
Let ADT = {a, b, c, d, (ð›‚) } be a dual trapezoidal fuzzy number whose membership function function is given as
µDT(x) =
To find ð›‚-cut of ADT .We first set ð›‚ [0,1] to both left and right reference functions of ADT. Expressing X in terms of 𛂠which gives ð›‚-cut of ADT.
[0,1] to both left and right reference functions of ADT. Expressing X in terms of 𛂠which gives ð›‚-cut of ADT.
ð›‚= 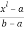
⇨ x l= a+ (b-a) ð›‚
ð›‚=
⇨ x r =d-(d-c) ð›‚
⇨ Að›‚DT= [a+ (b-a) ð›‚, d-(d-c) ð›‚]
In ordinary to find ð›‚-cut, we give 𛂠values as 0 or 0.5 or 1 in the interval [0, 1] .Instead of giving these values for ð›‚. we divide the interval [0,1] as many continuous subinterval. If we give very small values for ð›‚, the ð›‚-cut converges to a fuzzy number [a, d] in the domain of X it will be illustrated by example as given below.
Example
ADT = (-6,-4, 3, 6) and its membership function will be
µDT(x) =
α- cut of dual Trapezoidal fuzzy Number
𛂠= (x l + 6)/2
- Xl = 2ð›‚-6
𛂠= (6 – xr)/3
- Xr = 6-3ð›‚
- ADTð›‚=[ 2ð›‚-6, 6-3𛂠]
When ð›‚=1/10 then ADT𛂠= [-5. 8 , 5.7]
When ð›‚=1/102 then ADT =[-5.98 , 5.97]
When ð›‚=1/103 then ADT𛂠= [-5.998 , 5.997]
When ð›‚=1/104 then ADTð›‚=[-5.9998 , 5.9997]
When ð›‚=1/105 then ADTð›‚=[-5.99998 , 5.99997 ]
When ð›‚=1/106 then ADTð›‚=[ -5.999998 , 5.999997 ]
When ð›‚=1/107 then ADTð›‚=[ -5.9999998 , 5.9999997, ]
When ð›‚=1/108 then ADTð›‚=[ -5.99999998 , 5.99999997 ]
When ð›‚=1/109 then ADTð›‚=[ -5.999999998 , 5.999999997]
When ð›‚=1/1010 then ADTð›‚=[-6 , 6]
When ð›‚=1/1011 then ADTð›‚=[-6 , 6]
When ð›‚=1/1012 then ADT𛂠=[-6 , 6]
When ð›‚=1/1013 then ADT𛂠=[-6 , 6 ]
…………………………..etc
When ð›‚=1/10n as n →∞ then the ð›‚-cut converges to ADTð›‚=[-6, 6 ]

Figure: Graphical Representation of convergence of ð›‚-cut
When ð›‚=2/10 then ADTð›‚= [ -5.6,5.4 ]
When ð›‚=2/102 then ADTð›‚= [ -5.96,5.94 ]
When ð›‚=2/103 then ADTð›‚=[ -5.996,5.994 ]
When ð›‚=2/104 then ADTð›‚=[ , -5.9996,5.9994 ]
When ð›‚=2/105 then ADTð›‚=[ , -5.99996,5.99994 ]
When ð›‚=2/106 then ADTð›‚=[ , -5.999996,5.999994 ]
When ð›‚=2/107 then ADTð›‚=[-5.9999996, 5.9999994 , ]
When ð›‚=2/108 then ADTð›‚=[ , -5.99999996,5.99999994 ]
When ð›‚=2/109 then ADTð›‚=[ , -5.999999996,5.999999994 ]
When ð›‚=2/1010 then ADTð›‚=[ , -6,6 ]
When ð›‚=2/1011 then ADTð›‚=[ -6,6 ]
When ð›‚=2/1012 then ADTð›‚=[ -6,6 ]
When ð›‚=2/1013 then ADTð›‚=[ -6,6]
…………………………………etc
When ð›‚=2/10n as n →∞ then the ð›‚-cut converges to ADTð›‚=[ -6,6 ]

Simillarly, ð›‚=3/10n,4/10n,5/10n,6/10n,7/10n,8/10n,9/10n,10/10n upto these value n varies from 1to ∞ after 11/10n,12/10n…………………………………..100/10n as n varies from 2 to ∞ and101/10n,102/10n…………………………………. as n varies from 3 to ∞ and the process is goes on like this if we give the value for 𛂠it will converges to the dual trapezoidal fuzzy number[-6,6]
From the above example we conclude that , In general we have { K/10n} if we give different values for K as n- varies upto to ∞ if we give as n tends to ∞ then the values of ADT𛂠converges to the fuzzy number[a,d] in the domain X.
APPLICATIONS
In this section we have numerically solved some elementary problems of mensuration based on arithmetic operation using defuzzified centroid area method
Perimeter of Rectangle
Let the length and breadth of a rectangle are two positive dual trapezoidal fuzzy numbers ADT = (10cm, 11cm, 12cm,13cm) and BDT = (4cm, 5cm,6cm,7cm) then perimeter CDT of rectangle is 2[ADT+BDT]
Therefore the perimeter of the rectangle is a dual trapezoidal fuzzy number CDT = (28cm, 32cm,36cm,40cm) and its membership functions
µDT(x) =

The Perimeter of the rectangle is not less than 28 and not greater than 40 .The perimeter value takes between 32 to 36.
Centroid area method:
X* = 
= 
= 
= 
= 34
The approximate value of the perimeter of the rectangle is 34 cm.
2.Length of Rod:
Let length of a rod is a positive DTrFN ADT = (10cm,11cm,12cm, 13cm). If the length BDT = (5cm, 6cm , 7cm, 8cm), a DTrFN is cut off from this rod then the remaining length of the rod CDT is [ADT(-)BDT]
The remaining length of the rod is a DTrFN CDT = (2cm, 4cm, 6cm, 8cm) and its membership function
µDT(x) =
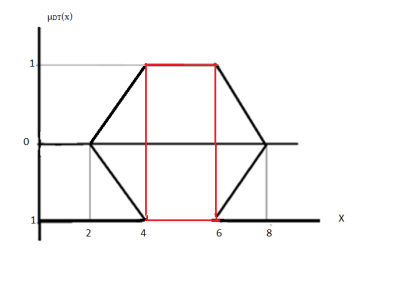
The remaining length of the rod is not less than 2cm and not greater than 8cm.The length of the rod takes the value between 4cm and 6cm.
Centroid area method:
X* = 
= 
= 
= 
= 5
The approximate value of the remaining length of the rod is 5cm.
Length of a Rectangle
Let the area and breadth of a rectangle are two positive dual trapezoidal fuzzy numbers ADT=(36cm,40cm,44cm,48cm) and BDT=(3cm,4cm,5cm,6cm) then the length CDT of the rectangle is is ADT(:)BDT.
Therefore the length of the rectangle is a dual trapezoidal fuzzy number CDT=(6cm,8cm,11cm,16cm) and its membership functions
µDT(x) =

The length of the rectangle is not less than 6cm and not greater than 16cm .The length of the rectangle takes the value between 8cm and 11cm.
Centroid area method:
X * = 
= 
= 
= 10.38
The approximate value of the length of the rectangle is 10.38cm.
Area of the Rectangle
Let the length and breadth of a rectangle are two positive dual trapezoidal fuzzy numbers ADT=(3cm,4cm,5cm,6cm) and BDT=(8cm,9cm,10cm,11cm) then the area of rectangle is ADT(.) BDT
Therefore the area of the rectangle is a dual trapezoidal fuzzy number CDT= (24cm, 36cm, 50cm, 66cm) and its membership functions
µDT(x) =

The area of the rectangle not less than 24 and not greater than 66.The area of the reactangle takes the value between 36 and 50.
Centroid area method:
X * = 
= 
= 
= 44.167sq.cm
CONCLUSION
In this paper, we have worked on DTrFN .We have define the Convergence of α-Cut to the fuzzy number. We have solved numerically some problems of mensuration based on operations using DTrFN and we have calculated the approximate values. Further DTrFN can be used in various problem of engineering and mathematical science.
References
- Sanhita Banerjee, Tapan Kumar Roy Arithmetic Operations on Generalized Trapezoidal Fuzzy Number and its Applications TJFS: Turkish Journal of Fuzzy Systems (eISSN: 1309–1190) An Official Journal of Turkish Fuzzy Systems Association Vol.3, No.1, pp. 16-44, 2012.
- Bansal. A., (2010), some non- linear arithmetic operations on triangular fuzzy number (m, α, β), Advances in Fuzzy Mathematics, 5,147-156.
- G. J. Klir, Bo Yuan, Fuzzy Sets and Fuzzy logic, Prentice Hall of India Private Limited, (2005).
- C. Parvathi, C. Malathi, Arithmetic operations on Symmetric Trapezoidal Intuitionistic Fuzzy Numbers, International Journal of Soft Computing and Engineering, 2 (2012) ISSN: 2231-2307.
- T. Pathinathan, K. Ponnivalavan, Pentagonal fuzzy numbers, International journal of computing algorithm, 3 (2014) ISSN: 2278-2397.
- Bansal Abhinav, Trapezoidal Fuzzy Numbers (a, b, c, d); Arithmetic Behavior, International Journal of Physical Mathematical Sciences, ISSN: 2010-1791.
- T. Pathinathan, K. Ponnivalavan, Diamond fuzzy numbers, International scientific Publications and consulting services journal of fuzzy set valued analysis http://www.ispacs.com/journals/jfsva/2014/jfsva-00220
- D. Dubois, H. Prade, Operations on Fuzzy Numbers, International Journal of Systems Science, 9 (6) (1978) 613-626. http://dx.doi.org/10.1080/00207727808941724.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal


